Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 9)
-
3114 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có: = + C
Vậy = ln|2x + 3| + C.
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vì = + ex + C nên:
f (x) = ![]() = x2 + ex.
= x2 + ex.
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Phương trình mặt cầu (S) là:
x2 + y2 + z2 − 6x + 4y − 8z + 4 = 0
Û (x − 3)2 + (y + 2)2 + (z − 4)2 = 25
Trong không gian Oxyz cho mặt cầu S tâm I (a; b; c) bán kính R.
Phương trình chính tắc của (S) là: (x − a)2 + (y − b)2 + (z − c)2 = R2.
Vậy nên tọa độ tâm I và bán kính R của mặt cầu (S) lần lượt là I (3; −2; 4) và R = 5.Câu 6:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có: J =
= 4 −
= 4.3 − = 12 − 3.2 = 6.Câu 7:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Hoành độ giao điểm của đường thẳng y = − x2 + 2x và trục Ox là:
− x2 + 2x = 0
Û x. (−x + 2) = 0
Û
Û
Thể tích của khối tròn xoay cần tìm là:
V =
Câu 8:
 Xem đáp án
Xem đáp án
Vì mặt phẳng (P) tiếp xúc với mặt cầu nên khoảng cách từ điểm I (1; 0; −2) đến mặt phẳng (P) là bán kính mặt cầu
d(I, (P)) = = 3.
Vậy bán kính mặt cầu (S) bằng 3.
Mặt cầu (S) có tâm I (1; 0; −2) và bán kính bằng 3 có phương trình là:
(x − 1)2 + y2 + (z + 2)2 = 9.
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Áp dụng tính chất của tích phân, ta có:
Do đó
Vậy
Câu 10:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Đặt u = 2x + 1 => du = 2dx
dv = exdx => v = ex + C
Chọn C = 0 => v = ex
Do đó I = − 2.Câu 11:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Trên mỗi trục tọa độ người ta quy ước các vectơ đơn vị
Tất cả các vectơ trong không gian đều được biểu diễn qua các vectơ đơn vị.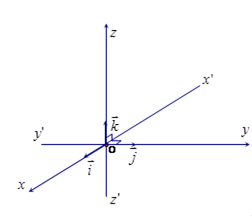
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vì mặt phẳng vuông góc với đường thẳng BC nên VTPT của mặt phẳng là :
= = (−4; 2; 0) = (2; −1; 0).
Phương trình mặt phẳng đi qua điểm A (0; 1; 2) và có VTPT = (−4; 2; 0) là:
2. (x − 0) − 1. (y − 1) + 0. (z − 2) = 0.
Vậy phương trình mặt phẳng đi qua A và vuông góc với BC là: 2x − y + 1 = 0.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Diện tích thiết diện là:
S = .2x. cosx = x. cosx
Thể tích vật thể B bằng: VB = .
Đặt u = x => du = dx
dv = cosxdx => v = sinx + C
Chọn C = 0 => v = sinx
Câu 15:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Công thức tính diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = f (x), trục Ox và các đường thẳng x = a, x = b (a < b) là:
.Câu 16:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Do F(x) là một nguyên hàm của hàm số f (x) = nên:
F(3) − F(2) = .
F(3) − 1 = = ln2 − ln1 = ln2 + 1.Câu 17:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vì là hình chiếu vuông góc của điểm A lên mặt phẳng (Oyz) nên tọa độ điểm hình chiếu của A là N (0; −1; 1).
Câu 18:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Mặt phẳng (MNP) đi qua ba điểm M (2; 0; 0), N (0; −1; 0) và P (0; 0; 2).
Nên mặt phẳng (MNP) có phương trình đoạn chắn là:
Câu 19:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Vì là mặt phẳng trung trực đoạn AB nên VTPT của mặt phẳng là vectơ :
= = (2; 2; 4) = (1; 1; 2)
Gọi I là trung điểm của đoạn AB.
xI = = = 2;
yI = = = 1;
zI = = = − 1.
Do đó điểm I có tọa độ là I (2; 1; −1).
Mặt phẳng có VTPT là = (1; 1; 2) và đi qua điểm I (2; 1; −1) là:
1.(x − 2) + 1. (y − 1) + 2. (z + 1) = 0
Û x – 2 + y – 1 + 2z + 2 = 0
Û x + y + 2z – 1 = 0
Vậy phương trình mặt phẳng là: x + y + 2z – 1 = 0.
Câu 20:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Hình phẳng giới hạn bởi đồ thị hàm số y = f (x) liên tục trên đoạn [a; b], trục Ox và hai đường thẳng x = a, x = b quay quanh Ox ta được khối tròn xoay có thể tích là:
V = π .
Vậy nên hình phẳng (D) được giới hạn bởi các đường x = 0, x = 1, y = 0 và y = có thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục Ox được tính theo công thức là: V = π .Câu 21:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có:
xG = = = 1;
yG = = = 2;
zG = = = 1.
Vậy tọa độ điểm G là G (1; 2; 1).
Câu 22:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Đặt u = lnx => du = dx
dv = x2dx => v = + C
Chọn C = 0 => v =
Câu 23:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Đáp án C sai do không có tích chất hay khái niệm nào của nguyên hàm quy định là:
= . .
Câu 24:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Đặt t = −x => dt = −dx.
Đổi cận:
![Cho f (x) là hàm số chẵn liên tục trong đoạn [−1; 1] và tích phân từ -1 đến 1 f(x) dx = 2. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/07/blobid0-1657901003.png)
Vậy I = 1.
Câu 25:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Nếu hàm số y = f (x) liên tục trên đoạn [a; b] thì diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b là:
S =
Vậy nên diện tích S hình phẳng giới hạn bởi các đường y = x3 + 2x + 1, trục hoành, x = 1 và x = 2 là:
S = .
Vì x3 + 2x + 1 > 0 khi x Î [1; 2] nên | x3 + 2x + 1| = x3 + 2x + 1.
Do đó:
