39 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 7)

Câu 1:

Họ tất cả các nguyên hàm của hàm số f(x) =

\frac{1}{x}

− 6x² là

A. $\ln |x| - 2 x^{3} + C$

B. $- \ln |x| - 2 x^{3} + C$

C. $- \frac{1}{x^{2}} - 12 x + C$

D. $\ln |x| - 6 x^{3} + C$

Xem đáp án

Đáp án đúng là: A

$\int (\frac{1}{x} - 6 x^{2}) d x = \int \frac{1}{x} d x - \int 6 x^{2} d x = \ln |x| - 2 x^{3} + C .$

Câu 2:

Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P) có phương trình là x + 2y – 4z + 1 = 0 và điểm M (1; 0; −2). Tính khoảng cách d₁ từ điểm M đến mặt phẳng (P) và tính khoảng cách d₂ từ điểm M đến mặt phẳng (Oxy).

A. $d_{1} = \frac{10 \sqrt{21}}{21} và d_{2} = 2$

B. $d_{1} = \frac{10 \sqrt{21}}{21} và d_{2} = 3$

C. $d_{1} = \frac{10}{\sqrt{20}} và d_{2} = 2$

D. $d_{1} = \frac{10}{\sqrt{20}} và d_{2} = 1$

Xem đáp án

Đáp án đúng là: A

(P): x + 2y – 4z + 1 = 0

Mặt phẳng (Oxyz) đi qua O, vectơ pháp tuyến $\vec{k}$ = (0; 0; 1) có phương trình là

1(z − 0) = 0 Û z = 0

Do đó

d₁ = d_(M;(P)) = $\frac{|1 + 2.0 - 4. (- 2) + 1|}{\sqrt{1^{2} + 2^{2} + 4^{2}}} = \frac{10 \sqrt{21}}{21}$ ;

d₂ = d_(M;(Oxy)) = $\frac{|- 2|}{\sqrt{1}}$ = 2.

Câu 3:

Tính I = $\int_{0}^{\frac{π}{4}} x \cos 2 x d x$

A. $I = - \frac{π}{8} + \frac{1}{4}$

B. $I = - \frac{π}{8} - \frac{1}{4}$

C. $I = \frac{π}{8} + \frac{1}{4}$

D. $I = \frac{π}{8} - \frac{1}{4}$

Xem đáp án

Đáp án đúng là: D

Đặt $\{\begin{matrix} u = x \\ d u = \cos 2 x d x \end{matrix}$ Û $\{\begin{matrix} d u = d x \\ v = \frac{1}{2} \sin 2 x \end{matrix}$

Do đó: I =

\int_{0}^{\frac{π}{4}} x \cos 2 x d x = {\frac{1}{2} x \sin 2 x|}_{0}^{\frac{π}{4}} - \frac{1}{2} \int_{0}^{\frac{π}{4}} \sin 2 x d x = \frac{π}{8} - \frac{1}{4}

Câu 4:

Trong không gian Oxyz, mặt phẳng (α) đi qua gốc tọa độ O(0; 0; 0) và có vectơ pháp tuyến là

\vec{n}

= (6; 3; −2) thì phương trình của (α) là

A. 6x – 3y – 2z = 0

B. −6x – 3y – 2z = 0

C. 6x + 3y – 2z= 0

D. −6x + 3y – 2z = 0

Xem đáp án

Đáp án đúng là: C

Phương trình mặt phẳng (α) đi qua O(0; 0; 0) và $\vec{n}$ = (6; 3; −2) là:

6(x − 0) + 3(y – 0) − 2(z – 0)= 0

Û 6x + 3y – 2z = 0

Vậy phương trình là 6x + 3y – 2z = 0.

Câu 5:

Cho

\int_{0}^{2} f (x) d x

= 3 và

\int_{0}^{2} g (x) d x

= −2. Khi đó

\int_{0}^{2} [2 f (x) - g (x)] d x

bằng

A. 1

B. 5

C. 4

D. 8

Xem đáp án

Đáp án đúng là: D

$\int_{0}^{2} [2 f (x) - g (x)] d x = \int_{0}^{2} f (x) d x - \int_{0}^{2} g (x) d x = 2.3 + 2 = 8$

Câu 6:

Cho hàm số y = f(x) liên tục trên ℝ và thỏa mãn

\int f (x) d x

= 4x³ – 3x²+ 2x + C. Hàm số f(x) là:

A. f(x) = x⁴ + x³ + x² + Cx + C'

B. f(x) = 12x² – 6x + 2

C. f(x) = x⁴ – x³ + x² + Cx

D. 12x² – 6x + 2 + C

Xem đáp án

Đáp án đúng là: B

Ta có $\int f (x) d x$ = 4x³ – 3x² + 2x + C.

Nên f(x) = 12x² – 6x + 2.

Câu 7:

Trong không gian với hệ tọa độ Oxyz, cho ba vectơ

\vec{b} = - 2 \vec{j} + 5 \vec{k}, \vec{c} = \vec{- i} - 3 \vec{j}

. Khẳng định nào sau đây đúng?

A.

\vec{b}

= (−2; 5; 0),

\vec{c}

= (−1; −3; 0).

B.

\vec{b}

= (−2; 5; 0),

\vec{c}

= (0; −3; 0).

C.

\vec{b}

= (0; −2; 5),

\vec{c}

= (−1; −3; 0).

D.

\vec{b}

= (1; −2; 5),

\vec{c}

= (−1; −3; 1).

Xem đáp án

Đáp án đúng là: C

$\vec{b} = - 2 \vec{j} + 5 \vec{k}$ = (0; −2; 5);

$\vec{c} = \vec{- i} - 3 \vec{j}$ = (−1; −3; 0).

Câu 8:

F(x) là một nguyên hàm của hàm số f(x) =

\frac{2 x + 3}{x^{2}}

(x ≠ 0), biết rằng F(1) = 1. F(x) là biểu thức nào sau đây ?

A. $F (x) = 2 \ln |x| - \frac{3}{x} - 4$

B. $F (x) = 2 \ln |x| + \frac{3}{x} + 2$

C. $F (x) = 2 x + \frac{3}{x} - 4$

D. $F (x) = 2 x - \frac{3}{x} + 2$

Xem đáp án

Đáp án đúng là: A

$\int \frac{2 x + 3}{x^{2}} d x = \int (\frac{2}{x} + \frac{3}{x^{2}}) d x = 2 \ln |x| - \frac{3}{x} + C$
Với F(1) = 1 , ta có:

2ln1 – 3 + C = 1 Û C = 4

Vậy I =

2 \ln |x| - \frac{3}{x} + 4

.

Câu 9:

Cho f(x) = 3x² + 2x – 3 có một nguyên hàm F(x) thỏa mãn F(1) = 0. Nguyên hàm đó là kết quả nào sau đây?

A. F(x) = x³ + x² – 3x

B. F(x) = x³ + x² – 3x + 1

C. F(x) = x³ + x² – 3x + 2

D. F(x) = x³ + x² – 3x – 1

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

$\int (3 x^{2} + 2 x - 3) d x$ = x³ + x² – 3x + C

Với F(1) = 0, ta có: 1³ + 1² – 3.1 + C = 0 Û C = 1.

Vậy nguyên hàm đó là : x³ + x² – 3x + 1.

Câu 10:

Họ nguyên hàm của hàm số f(x) = 2x (1 + 3x³) là

A. $x^{2} (1 + \frac{6 x^{3}}{5}) + C$

B. $2 x (x + \frac{3}{4} x^{4}) + C$

C. $x^{2} (x + \frac{3}{4} x^{3}) + C$

D. $x^{2} (1 + \frac{3}{2} x^{2}) + C$

Xem đáp án

Đáp án đúng là: A

$\int (2 x + 6 x^{4}) dx = \int 2 xdx + \int 6 x^{4} dx = x^{2} + \frac{6}{5} x^{5} + C = x^{2} (1 + \frac{6}{5} x^{3}) + C$

Câu 11:

Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt cầu (S) có tâm I(2; 1; 2) và bán kính R = 3.

A. (S): (x + 2)² + (y + 1)² + (z + 2)² = 9

B. (S): (x – 2)² + (y – 1)² + (z – 2)² = 9

C. (S): (x + 2)² + (y + 1)² + (z + 2)² = 3

D. (S): (x – 2)² + (y – 1)² + (z – 1)² = 3

Xem đáp án

Đáp án đúng là: B

Phương trình mặt cầu (S) có tâm I(2; 1; 2) và bán kính R = 3 là:

(x – 2)² + (y – 1)² + (z – 2)² = 9.

Câu 12:

Với tích phân I =

\int x \cos 2 x d x

sử dụng công thức từng phần và đặt

\{\begin{matrix} u = x \\ d v = \cos 2 x d x \end{matrix}

thì sẽ được

A. I =

x \frac{s in 2 x}{2} + \frac{1}{2} \int s in2xdx

B. I =

- x \frac{\sin 2 x}{2} - \frac{1}{2} \int \sin 2 x d x

C. I =

- x \frac{\sin 2 x}{2} + \frac{1}{2} \int \sin 2 x d x

D. I =

x \frac{\sin 2 x}{2} - \frac{1}{2} \int \sin 2 x d x

Xem đáp án

Đáp án đúng là: D

Đặt $\{\begin{matrix} u = x \\ d v = \cos 2 x d x \end{matrix}$ Û $\{\begin{matrix} d u = d x \\ v = \frac{1}{2} \sin 2 x \end{matrix}$

Do đó I = $\int x \cos 2 x d x$ = $x \frac{\sin 2 x}{2} - \frac{1}{2} \int \sin 2 x d x$ .

Câu 13:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(2; 2; 1). Tính độ dài đoạn thẳng OA.

A. OA = $\sqrt{5}$

B. OA = 5

C. OA = 3

D. OA = 9

Xem đáp án

Đáp án đúng là: C

Độ dài đoạn thẳng OA là:

OA =

\sqrt{2^{2} + 2^{2} + 1}

= 3.

Câu 14:

Cho hàm số f(x) liên tục trên ℝ và F(x) là nguyên hàm của f(x), biết

\int_{0}^{9} f (x) dx

= 9 và F(0) = 3. Tính F(9)

A. F(9) = −6

B. F(9) = −12

C. F(9) = 6

D. F(9) = 12

Xem đáp án

Đáp án đúng là: D

$\int_{0}^{9} f (x) dx$ = ${F (x)|}_{0}^{9}$ = F(9) – F(0) = 9

Û F(9) – 3 = 9 Û F(9) = 12.

Câu 15:

Cho hàm số f(x) có f '(x) liên tục trên đoạn [−1; 3], f(−1) = 4 và

\int_{- 1}^{3} f' (x) dx

= 10. Giá trị của f(3) bằng

A. 6

B. -14

C. -6

D. 14

Xem đáp án

Đáp án đúng là: D

$\int_{- 1}^{3} f' (x) dx = {f (x)|}_{- 1}^{3}$ = f(3) – f(−1) = 10

Û f(3) – 4 = 10 Û f(3) = 14.

Câu 16:

Biết

\int_{1}^{5} f (x) d x

= 4. Giá trị của

\int_{1}^{5} 3 f (x) d x

bằng

A. 64

B. 12

C. 7

D. $\frac{4}{3}$

Xem đáp án

Đáp án đúng là: B

\int_{1}^{5} 3 f (x) dx

= 3

\int_{1}^{5} f (x) dx

= 3.4 = 12

Câu 17:

Trong không gian với hệ trục tọa độ Oxyz, cho điểm I(2; −2; 0) và điểm M(1; 0; 2). Phương trình mặt cầu tâm I đi qua M là

A. (x – 2)² + (y + 2)² + z² = 3

B. (x + 2)² + (y – 2)² + z²= 9

C. (x – 2)² + (y + 2)² + z² = 9

D. (x – 2)² + (y + 2)² + z² = 3

Xem đáp án

Đáp án đúng là: C

Ta có IM = R = $\sqrt{{(1 - 2)}^{2} + {(0 + 2)}^{2} + {(2 - 0)}^{2}} = 3$

Phương trình mặt cầu (P) tâm I(2; −2; 0) có R = 3 là:

(P): (x – 2)²+ (y + 2)² + z² = 9

Câu 18:

Cho hàm số f(x) có đạo hàm cấp hai trên [2; 4] thỏa mãn f '(2) = 1 và f '(4) =5. Khi đó

\int_{2}^{4} f " (x) d x

bằng

A. 3

B. 1

C. 4

D. 2

Xem đáp án

Đáp án đúng là: C

\int_{2}^{4} f " (x) dx

=

{f' (x)|}_{2}^{4}

= f '(4) – f '(2) = 5 – 1 = 4

Câu 19:

Cho

\int_{- 2}^{2} f (x) dx = 1

,

\int_{- 2}^{4} f (t) dt = - 4

. Tính

\int_{2}^{4} f (y) dy

A. I = 3

B. I = −5

C. I = 5

D. I = −3

Xem đáp án

Đáp án đúng là: B

Ta có: $\int_{a}^{b} f (x) dx = \int_{a}^{b} f (t) dt = \int_{a}^{b} f (y) dy$

\int_{2}^{4} f (y) dy = \int_{- 2}^{4} f (x) dx + \int_{2}^{- 2} f (t) dt

= −4 − 1 = −5.

Câu 20:

Họ tất cả các nguyên hàm của hàm số f(x) =

\frac{x + 2}{x - 1}

trên khoảng (1; +∞) là

A. x + 3ln(x – 1) + C

B. x – 3ln(x – 1) + C

C. x − $\frac{3}{{(x - 1)}^{2}}$ + C

D. x + $\frac{3}{{(x - 1)}^{2}}$ + C

Xem đáp án

Đáp án đúng là: A

$\int \frac{x + 2}{x - 1} d x = \int \frac{x - 1 + 3}{x - 1} = \int (1 + \frac{3}{x - 1}) d x$

= x + 3ln(x – 1) + C.

Câu 21:

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): 3x – my – z + 7 = 0 và mặt phẳng (Q): 6x + 5y – 2z – 4 =0. Hai mặt phẳng (P) và (Q) song song với nhau khi giá trị m bằng bao nhiêu?

A. m = -30

B.

m = \frac{5}{2}

C. m = 4

D.

m = - \frac{5}{2}

Xem đáp án

Đáp án đúng là: D

Ta có (P) // (Q) khi: $\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'}$ ≠ $\frac{d}{d'}$

$\Leftrightarrow \frac{3}{6} = \frac{- m}{5} = \frac{- 1}{- 2} \Leftrightarrow \frac{- m}{5} = \frac{1}{2} \Leftrightarrow m = - \frac{5}{2} .$

Câu 22:

Nguyên hàm của hàm số f(x) = sin(1 – 3x) là

A.

- \frac{1}{3} \cos (1 - 3 x) + C

B. 3cos(1 −3x) + C

C. −3cos(1 – 3x) + C

D.

\frac{1}{3}

cos(1 – 3x) + C

Xem đáp án

Đáp án đúng là: D

$\int \sin (1 - 3 x) dx = - \frac{1}{3} [- \cos (1 - 3 x)] dx = \frac{1}{3} \cos (1 - 3 x) + C$

Câu 23:

Cho

\int_{0}^{\frac{π}{2}} f (x) dx = 3

. Tính I =

\int_{0}^{\frac{π}{2}} [2 f (x) + s inx] dx

A. I = 4

B. I = 7

C. I = 6

D. I = 5

Xem đáp án

Đáp án đúng là: B

$\int_{0}^{\frac{π}{2}} [2 f (x) + s inx] dx$ = 2 $\int_{0}^{\frac{π}{2}} f (x) dx + \int_{0}^{\frac{π}{2}} \sin x dx$ = 2. 3 + 1 = 7

Câu 24:

Trong không gian Oxyz, cho hai vectơ

\vec{a}

= (−3; 1; 0) và

\vec{b}

= (0; 1; −2). Vectơ

\vec{a} + \vec{b}

có tọa độ là

A. (−3; 2; 2)

B. (−3; 2; −2)

C. (−3; 0; −2)

D. (−3; 0; 2)

Xem đáp án

Đáp án đúng là: B

\vec{a} + \vec{b}

= (−3 + 0; 1 + 1; 0 – 2) = (−3; 2; −2).

Câu 25:

Tìm

\int \frac{1}{x^{2}} d x

A. $\int \frac{1}{x^{2}} dx = \frac{1}{2 x} + C$

B. $\int \frac{1}{x^{2}} dx = {lnx}^{2} + C .$

C. $\int \frac{1}{x^{2}} dx = \frac{1}{x} + C$

D. $\int \frac{1}{x^{2}} dx = - \frac{1}{x} + C$

Xem đáp án

Đáp án đúng là: D

Ta có $\int \frac{1}{x^{2}} d x = - \frac{1}{x} + C$ .

Câu 26:

Nếu

\int_{1}^{3} [2 f (x) + 1] d x = 5

thì

\int_{1}^{3} f (x) d x

bằng

A. 3

B. 2

C. $\frac{3}{4}$

D. $\frac{3}{2}$

Xem đáp án

Đáp án đúng là: D

$\int_{1}^{3} [2 f (x) + 1] d x = 2 \int_{1}^{3} f (x) d x + \int_{1}^{3} 1 d x$ = 5

Û 2 $\int_{1}^{3} f (x) d x$ + ${x|}_{1}^{3}$ = 5

Û 2 $\int_{1}^{3} f (x) d x$ = 3

\Leftrightarrow \int_{1}^{3} f (x) d x

=

\frac{3}{2}

.

Câu 27:

Họ tất cả các nguyên hàm của hàm số f(x) = 3^x + sin8x là

A. $\frac{3^{x}}{\ln 3} - \cos 8 x + C$

B. $\frac{3^{x}}{\ln 3} - \frac{1}{8} \cos 8 x + C$

C. $\frac{3^{x}}{\ln 3} + \frac{1}{8} \cos 8 x + C$

D. 3^xln3

- \frac{1}{8} \cos 8 x + C

Xem đáp án

Đáp án đúng là: B

Ta có $\int (3^{x} + \sin 8 x) d x$ = $\int 3^{x} dx + \int \sin 8 xdx$

=

\frac{3^{x}}{\ln 3} - \frac{1}{8} \cos 8 x + C

.

Câu 28:

Tính I =

\int_{0}^{\frac{π}{4}} \frac{\cos 2 x}{1 + 2 \sin 2 x} d x

A. $I = \frac{1}{2} \ln 3$

B. $I = \frac{1}{3} \ln 3$

C. $I = \frac{1}{4} \ln 3$

D. $I = \frac{1}{5} \ln 3$

Xem đáp án

Đáp án đúng là: C

Đặt u = 1 + 2sin2x Û du = 4cos2xdx

Do đó: I = $\int_{0}^{\frac{π}{4}} \frac{\cos 2 x}{1 + 2 \sin 2 x} d x$ = cos2xdx = $\frac{1}{4}$ du

Đổi cận :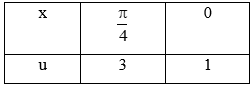

Tính I = tích phân từ 0 đến pi/4 cos2x/1+2sin2x dx (ảnh 1)

Do đó: I = $\int_{1}^{3} \frac{1}{u} . \frac{1}{4} du$ = $\frac{1}{4} {\ln |u||}_{1}^{3}$

= $\frac{1}{4} (\ln 3 - \ln 1)$ = $\frac{\ln 3}{4}$ .

Câu 29:

Giá trị m để hàm số F(x) = mx³ + (3m + 2)x² – 4x + 3 là một nguyên hàm của hàm số f(x) = 3x² + 10x – 4 là

A. m = 3

B. m = 0

C. m = 1

D. m = 2

Xem đáp án

Đáp án đúng là: C

Ta có F(x) = mx³ + (3m + 2)x² – 4x + 3 nên:

f(x) = 3mx² + 2(3m + 2)x − 4 = 3x² + 10x – 4.

Û $\{\begin{matrix} 3 m = 3 \\ 2 (3 m + 2) = 10 \end{matrix} \Leftrightarrow$ m =1

Câu 30:

Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) song song với giá trị của 2 vectơ là

\vec{u_{1}}

= (4; 1; 2) và

\vec{u_{2}}

= (1; 2; −1). Vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng (P) ?

A.

\vec{n}

= (5; −6; 7)

B.

\vec{n}

= (−5; 6; 7)

C.

\vec{n}

= (−5; 6; −7)

D.

\vec{n}

= (5; −6; 7)

Xem đáp án

Đáp án đúng là: B

Vectơ $\vec{u_{1}}$ = (4; 1; 2), $\vec{u_{2}}$ = (1; 2; −1).

Nên ta có:

[\vec{u_{1}}, \vec{u_{2}}]

= ( −5; 6; 7).

Câu 31:

Cho

\int_{0}^{1} x \sqrt{28 x^{2} + 1} dx = \frac{m . \sqrt{29} + n}{84}

với m và n là số nguyên. Tính k = m + n

A. k = 28

B. k = 0

C. k = 30

D. k = 2

Xem đáp án

Đáp án đúng là: A

Đặt u = $\sqrt{28 x^{2} + 1}$ (u ≥ 0) Û u² = 28x² + 1

Û 2udu = 56xdx Þ udu = 28xdx.

Đổi cận: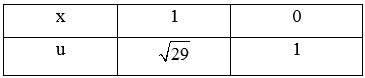

Cho tích phân từ 0 đến 1 x căn bậc hai 28x^2+1 dx = m.căn bậc hai 29 + n/ 84 với m và n là số nguyên. Tính k = m + n (ảnh 1)

Do đó: $\int_{0}^{1} x \sqrt{28 x^{2} + 1} dx = \frac{1}{28} . \int_{1}^{\sqrt{29}} u^{2} du = {\frac{1}{28} . \frac{u^{3}}{3}|}_{1}^{\sqrt{29}}$

= \frac{1}{28} . [\frac{{(\sqrt{29})}^{3}}{3} - \frac{1^{3}}{3}] = \frac{29 \sqrt{29} - 1}{84}

Do đó m = 29, n = −1.

Vậy k = m + n = 28.

Câu 32:

Trong không gian Oxyz, cho mặt phẳng (P): 2x – 3y + 6z + 19 = 0 và điểm A(−2; 4; 3). Gọi d là khoảng cách từ A đến mặt phẳng (P). Khi đó d bằng

A. 2

B. 1

C. 3

D. 4

Xem đáp án

Đáp án đúng là: C

d_(A;(P)) =

\frac{|2. (- 2) - 3.4 + 6.3 + 19|}{\sqrt{2^{2} + 3^{2} + 6^{2}}} = \frac{21}{7}

= 3.

Câu 33:

Cho

\int_{1}^{2} f (x) dx = - 3

và

\int_{2}^{3} f (x) dx = 4

. Khi đó

\int_{1}^{3} f (x) dx

bằng

A. 1

B. -12

C. 12

D. 7

Xem đáp án

Đáp án đúng là: A

\int_{1}^{3} f (x) dx = \int_{2}^{3} f (x) dx + \int_{1}^{2} f (x) dx

= 4 – 3 = 1.

Câu 34:

Nguyên hàm I =

\int 3 x \sqrt{7 - 3 x^{2}} dx

là

A. $I = - \frac{{(\sqrt{7 - 3 x^{2}})}^{3}}{3} + C$

B. $I = \frac{{(\sqrt{7 - 3 x^{2}})}^{3}}{3} + C$

C. $I = - 3 {(\sqrt{7 - 3 x^{2}})}^{3} + C$

D. $I = - {(\sqrt{7 - 3 x^{2}})}^{3} + C$

Xem đáp án

Đáp án đúng là: A

Đặt u = $\sqrt{7 - 3 x^{2}}$ (u ≥ 0) Û u² = 7 – 3x²

Û 2udu = −6xdx Þ 3xdx = −udu.

Do đó I = $\int 3 x \sqrt{7 - 3 x^{2}} dx = - \int u^{2} du$

= $- \frac{u^{3}}{3} = - \frac{{(\sqrt{7 - 3 x^{2}})}^{3}}{3} + C$

Câu 35:

Tích phân I =

\int_{0}^{2} \frac{1}{2 \sqrt{x + 2}} dx

bằng

A. I = $2 \sqrt{2}$

B. I = $2 - \frac{1}{\sqrt{2}}$

C. I = $2 - \sqrt{2}$

D. I = $1 - \frac{1}{\sqrt{2}}$

Xem đáp án

Đáp án đúng là: C

Đặt u = $\sqrt{x + 2}$ (u ≥ 0) Û u² = x + 1 Þ 2udu = dx.

Đổi cận:

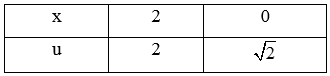
Tích phân I = tích phân từ 0 đến 2 1/2 căn bậc hai x + 2 bằng (ảnh 1)

Do đó:

\int_{0}^{2} \frac{1}{2 \sqrt{x + 2}} dx = \frac{1}{2} \int_{\sqrt{2}}^{2} 2 u^{2} du

= \int_{\sqrt{2}}^{2} u^{2} du = {(\frac{u^{3}}{3})|}_{\sqrt{2}}^{2} = 2 - \sqrt{2}

Câu 36:

Tìm nguyên hàm I =

\int {xe}^{3 x} dx

.

Xem đáp án

Đặt $\{\begin{matrix} u = x \\ dv = e^{3 x} dx \end{matrix}$ Û $\{\begin{matrix} du = dx \\ v = \frac{1}{3} e^{3 x} \end{matrix}$

Do đó: I = $\int {xe}^{3 x} dx = \frac{1}{3} {xe}^{3 x} - \frac{1}{3} \int e^{3 x} dx$

= $\frac{1}{3} x e^{3 x} - \frac{1}{9} e^{3 x} + C$ .

Câu 37:

Cho hình chóp S. ABC có đáy ABC là tam giác vuông, biết BA = BC = 2a, cạnh bên SA =

2 a \sqrt{2}

vuông góc với đáy. Tính diện tích mặt cầu ngoại tiếp hình chóp theo a.

Xem đáp án

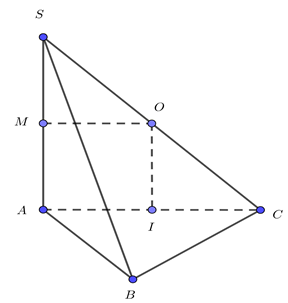
Cho hình chóp S. ABC có đáy ABC là tam giác vuông, biết BA = BC = 2a, cạnh bên (ảnh 1)

Cách 1.

Ta có: BC ^ SA, BC ^ AB Þ BC ^ SB.

Ta có: $\hat{S A C} = \hat{S B C}$ = 90°.

Khi đó 4 điểm S, A, B, C nằm trên mặt cầu đường kính SC.

Bán kính mặt cầu R = $\frac{S C}{2}$ = 2a.

Diện tích mặt cầu ngoại tiếp hình chóp S = 4π(2a)² = 16πa².

Cách 2.

Gọi I là tâm đường tròn ngoại tiếp tam giác ABC, do tam giác ABC vuông tại B nên I là trung điểm của AC.

Qua I dựng đường thẳng d vuông góc với (ABC) nên ta được d // SA.

Trong tam giác SAC, dựng đường trung trực của SA cắt d tại O là tâm mặt cầu ngoại tiếp hình chóp S. ABC.

Ta tính được AC = 2a $\sqrt{2}$ , SC = 4a.

Bán kính mặt cầu R = OA = $\sqrt{2 a^{2} + 2 a^{2}}$ = 2a.

Diện tích mặt cầu ngoại tiếp hình chóp S.ABC là:

S = 4π(2a)² = 16πa².

Câu 38:

Cho F(x) = (x – 1)e^x là một nguyên hàm của hàm số f(x)e^2x. Tìm nguyên hàm của hàm số f '(x)e^2x

Xem đáp án

Do F(x) = (x – 1)e^x là một nguyên hàm của f(x)e^2x nên:

F '(x) = f(x)e^2x

Û xe^x = f(x)e^2x

Û f(x) = $\frac{x}{e^{x}}$ .

Suy ra : f '(x) = $\frac{e^{x} - {xe}^{x}}{{(e^{x})}^{2}} = \frac{(1 - x) e^{x}}{e^{2 x}}$

Þ f '(x) = (1 – x)e^x.

Khi đó $\int f' (x) e^{2 x} dx = \int (1 - x) e^{x} dx$

Đặt $\{\begin{matrix} u = 1 - x \\ dv = e^{x} dx \end{matrix} \Leftrightarrow \{\begin{matrix} du = - dx \\ v = e^{x} \end{matrix}$

Do đó: $\int f' (x) e^{2 x} dx$ = (1 – x)e^x + $\int e^{x} dx$

= (1 – x)e^x + e^x = (2 – x)e^x + C.

Câu 39:

Cho hàm số f(x) có đạo hàm liên tục trên tập hợp

ℝ

thỏa mãn

\int_{1}^{2} f (3 x - 6) dx

= 3 và f(−3) = 2. Tính tích phân

\int_{- 3}^{0} xf' (x) dx

.

Xem đáp án

Đặt t = 3x – 6 Û dt = 3dx

Đổi cận :

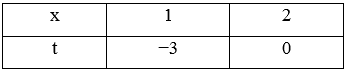
Cho hàm số f(x) có đạo hàm liên tục trên tập hợp R thỏa mãn tích phân từ 1 đến 2 f(3x-6)dx = 3 (ảnh 1)

Do đó: $\int_{1}^{2} f (3 x - 6) dx = \int_{1}^{2} f (3 x - 6) dx = \frac{1}{3} \int_{- 3}^{0} f (t) dt$ = 3

Þ $\int_{- 3}^{0} f (t) dt = 9 \Rightarrow \int_{- 3}^{0} f (x) dx = 9$

Đặt $\{\begin{matrix} u = x \\ dv = f' (x) dx \end{matrix} \Leftrightarrow \{\begin{matrix} du = dx \\ v = f (x) \end{matrix}$

Do đó: $\int_{- 3}^{0} xf' (x) dx = {xf (x)|}_{- 3}^{0} - \int_{- 3}^{0} f (x) dx$

= 0.f(0) + 3.f(−3) – 9 = −3.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất)

Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 7)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương