50 câu hỏi trắc nghiệm thuộc Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 10)

Câu 1:

Gọi S là diện tích của hình phẳng giới hạn bởi các đồ thị hàm số y = x² + 3 và y = 4x. Xác định mệnh đề đúng:

A. S =

\int_{1}^{3} |x^{2} + 4 x + 3| dx

B. S =

\int_{1}^{3} |- x^{2} - 4 x + 3| dx

C. S =

\int_{1}^{3} (x^{2} - 4 x + 3) dx

D. S =

\int_{1}^{3} (|x^{2} + 3| - |4 x|) dx

Xem đáp án

Đáp án đúng là: B

Phương trình trục hoành :

x² + 3 = 4x

Û x² + 3 – 4x = 0

Û $[\begin{matrix} x = 3 \\ x = 1 \end{matrix}$

Do đó diện tích của hình phẳng là: S = $\int_{1}^{3} |x^{2} - 4 x + 3| dx$

Câu 2:

Trong không gian Oxyz, cho hai điểm A(1; 1; −1) và B(2; 3; 2). Vectơ

\vec{AB}

có tọa độ là:

A. (−1; −2; 3)

B. (1; 2; 3)

C. (3; 5; 1)

D. (3; 4; 1)

Xem đáp án

Đáp án đúng là: B

Ta có $\vec{AB}$ = (2 – 1; 3 – 1; 2 + 1) = (1; 2; 3).

Câu 3:

Trong không gian Oxyz, mặt phẳng đi qua A(1; 0; 0), B(0; 2; 0), C(0; 0; 3) có phương trình là:

A. $\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 0$

B. $\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = - 1$

C. $\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1$

D. $\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 6$

Xem đáp án

Đáp án đúng là: C

Mặt phẳng đi qua A(1; 0; 0), B(0; 2; 0), C(0; 0; 3) có phương trình là:

\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1

Câu 4:

Mặt phẳng x + 2y – 3z = 0 không đi qua điểm nào dưới đây?

A. M(1; 1; 1)

B. Q(2; −1; 0)

C. P(−1; 2; 1)

D. N(1; 2; 3)

Xem đáp án

Đáp án đúng là: D

Thay các điểm và mặt phẳng sao cho mặt phẳng có giá trị khác 0 thì sẽ không đi qua mặt phẳng

Thay điểm N(1; 2; 3) vào mặt phẳng : 1 + 2.2 – 3.3 = – 4 ≠ 0.

Vậy N(1; 2; 3) không thuộc mặt phẳng x + 2y – 3z = 0.

Câu 5:

Trong không gian Oxyz, cho hai điểm A(2; −4; 3) và B(2; 2; 7). Trung điểm của đoạn thẳng AB có tọa độ là:

A. (4; −2; 10)

B. (2; 6; 4)

C. (2; −1; 5)

D. (1; 3; 2)

Xem đáp án

Đáp án đúng là: C

Trung điểm của đoạn thẳng AB là :

$\{\begin{matrix} x = \frac{2 + 2}{2} \\ y = \frac{- 4 + 2}{2} \\ z = \frac{3 + 7}{2} \end{matrix} \Leftrightarrow \{\begin{matrix} x = 2 \\ y = - 1 \\ z = 5 \end{matrix}$

Vậy trung điểm đoạn thẳng AB có tọa độ là (2; −1; 5).

Câu 6:

Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, x = 1, đồ thị hàm số y = x và trục Ox là:

A. S =

\frac{1}{4}

B. S = 2

C. S = 1

D. S =

\frac{1}{2}

Xem đáp án

Đáp án đúng là: D

Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, x = 1, đồ thị hàm số y = x và trục Ox là:

$\int_{0}^{1} |x| dx = {\frac{x^{2}}{2}|}_{0}^{1} = \frac{1}{2}$

Câu 7:

Cho f(x) là hàm số liên tục trên [a; b] và F(x) là một nguyên hàm của f(x). Khẳng định nào sau đây đúng?

A.

\int_{a}^{b} f (x) dx

= f(b) – f(a)

B.

\int_{a}^{b} f (x) dx

= −F(b) – F(a)

C.

\int_{a}^{b} f (x) dx

= F(a) – F(b)

D.

\int_{a}^{b} f (x) dx

= F(b) – F(a)

Xem đáp án

Đáp án đúng là: D

Ta có $\int_{a}^{b} f (x) dx$ = ${F (x)|}_{a}^{b}$ = F(b) – F(a).

Câu 8:

Cho

\int_{1}^{3} f (x) dx

= 2, giá trị của

\int_{0}^{1} f (2 x + 1) dx

bằng

A. 1

B. 4

C. 2

D. 3

Xem đáp án

Đáp án đúng là: A

Đặt u = 2x + 1 Û du = 2dx Þ dx = $\frac{1}{2}$ du

Đổi cận:

x	1	0
u	3	1

Ta có:

\int_{1}^{3} f (u) \frac{1}{2} du = \frac{1}{2} \int_{1}^{3} f (u) du = \frac{1}{2} \int_{1}^{3} f (x) dx = \frac{1}{2} . 2 = 1

Câu 9:

Cho

\int \frac{2 x + 1}{x - 2} dx

= ax + bln

|x - 2|

với a, b Î ℚ, giá trị của S = a + b là

A. S = 4

B. S = 7

C. S = 1

D. S = 2

Xem đáp án

Đáp án đúng là: B

$\int \frac{2 x + 1}{x - 2} dx = \int (2 + \frac{5}{x - 2}) dx$

= 2x + $5 \ln |x - 2|$ + C.

Do đó a = 2, b = 5.

Vậy S = a + b = 2 + 5 = 7.

Câu 10:

Khẳng định nào sau đây sai?

A. $\int lnxdx = \frac{1}{x} + C$

B. $\int e^{x} dx = e^{x} + C$

C. $\int xdx = \frac{x^{2}}{2} + C$

D. $\int \frac{1}{x} dx = \ln |x| + C$

Xem đáp án

Đáp án đúng là: A

Ta có:

\int \frac{1}{x} dx = \ln |x|

+ C nên đáp án A sai.

Câu 11:

Trong không gian với hệ tọa độ Oxyz, cho điểm A(2; 2; 1). Tính độ dài đoạn thẳng OA?

A. OA = 4

B. OA = 9

C. OA = 5

D. OA = 3

Xem đáp án

Đáp án đúng là: D

Ta có : A(2; 2; 1) và O(0; 0; 0).

Nên OA =

\sqrt{2^{2} + 2^{2} + 1}

= 3.

Câu 12:

Giá trị của I =

\int_{1}^{2} xdx

là:

A. 1

B. −1

C.

\frac{3}{2}

D. $\frac{2}{3}$

Xem đáp án

Đáp án đúng là: C

Ta có $\int_{1}^{2} xdx = {\frac{x^{2}}{2}|}_{1}^{2} = = \frac{2^{2}}{2} - \frac{1^{2}}{2} = \frac{3}{2}$

Câu 13:

Điều kiện của m để phương trình: x² + y² + z² – 2x + 2y + 4z + m = 0 là phương trình một mặt cầu là:

A. m < 6

B. m ≥ 6

C. m > 6

D. m ≤ 6

Xem đáp án

Đáp án đúng là: A

Ta có phương trình:x² + y² + z² – 2x + 2y + 4z + m = 0.

Điều kiện để phương trình là một mặt cầu:

Phương trình được viết thành: (x – 1)² + (y + 1)² + (z + 2)² = 6 – m

R > 0 Û 6 – m > 0 Û m < 6

Câu 14:

Khoảng cách giữa hai mặt phẳng 2x – y + 2z + 1 = 0 và 2x – y + 2z – 1 = 0 là

A. 0

B.

\frac{3}{2}

C. 1

D.

\frac{2}{3}

Xem đáp án

Đáp án đúng là: D

Gọi (P): 2x – y + 2z + 1= 0

(Q) : 2x – y + 2z – 1= 0

Lấy điểm M (−2; −1; 1)

d_((P);(Q)) = d_(M;(Q)) =

\frac{|2. (- 2) + 2. (- 1) + 4.1 - 1|}{\sqrt{2^{2} + 1 + 2^{2}}} = \frac{2}{3}

Câu 15:

Diện tích của hình phẳng (H) được giới hạn đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b (a < b) (phần tô đậm trong hình vẽ) được tính theo công thức:

Diện tích của hình phẳng (H) được giới hạn đồ thị hàm số y = f(x), trục hoành và hai đường thẳng (ảnh 1)

A. $S = \int_{a}^{c} f (x) dx + \int_{c}^{b} f (x) dx$

B. $S = \int_{a}^{b} f (x) dx$

C. $S = |\int_{a}^{b} f (x) dx|$

D. $S = - \int_{a}^{c} f (x) dx + \int_{c}^{b} f (x) dx$

Xem đáp án

Đáp án đúng là: D

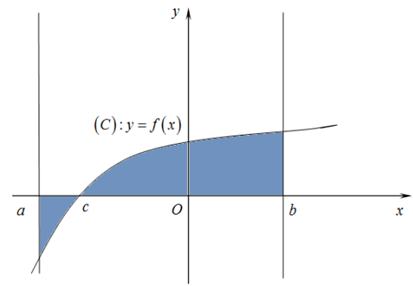
Từ đồ thị hàm số, ta thấy:

Từ x Î [a; c] nằm dưới trục hoành.

Từ x Î [c; b] nằm trên trục hoành.

Áp dụng công thức diện tích hình phẳng ta có:

$S = \int_{a}^{b} |f (x)| dx = \int_{a}^{c} [0 - f (x)] dx + \int_{c}^{b} [f (x) - 0] dx = - \int_{a}^{c} f (x) dx + \int_{c}^{b} f (x) dx$

Câu 16:

Cho

\int_{1}^{2} f (x) dx

= 3, giá trị của

\int_{1}^{2} [2 x + f (x)] dx

là:

A. 3

B. 6

C. 5

D. 4

Xem đáp án

Đáp án đúng là: B

$\int_{1}^{2} [2 x + f (x)] dx = \int_{1}^{2} 2 xdx + \int_{1}^{2} f (x) dx = {x^{2}|}_{1}^{2} + 3 = 6$

Câu 17:

Cho $\int_{1}^{2} f (x) dx$ = 4 và $\int_{- 1}^{2} f (x) dx$ = 5, giá trị của $\int_{- 1}^{1} f (x) dx$ là

A. 9

B. 1

C. 6

D. 5

Xem đáp án

Đáp án đúng là: B

$\int_{- 1}^{1} f (x) dx = \int_{2}^{1} f (x) dx + \int_{- 1}^{2} f (x) dx = - 4 + 5 = 1$

Câu 18:

Trong không gian Oxyz, hình chiếu vuông góc của điểm M(3; −1; 1) trên trục Oz có tọa độ là

A. (3; −1; 0)

B. (0; −1; 0)

C. (0; 0; 1)

D. (3; 0; 0)

Xem đáp án

Đáp án đúng là: C

Hình chiếu vuông góc của điểm M(3; −1; 1) trên trục Oz có tọa độ là (0; 0; 1).

Câu 19:

Khẳng định nào sau đây đúng?

A.

\int \sin x dx

= cosx + C

B.

\int \sin x dx

= sinx + C

C.

\int cosdx

= sinx + C

D.

\int cosdx

= −sinx + C

Xem đáp án

Đáp án đúng là: C

Ta có $\int cosxdx$ = sinx + C.

Do đó chọn đáp án C.

Câu 20:

Nguyên hàm của hàm số f(x) = 2^x là:

A. F(x) =

\frac{2^{x}}{\ln 2}

+ C

B. F(x) = 2^{x – 1} + C

C. F(x) = −2^x + C

D. F(x) = 2^x + C

Xem đáp án

Đáp án đúng là: A

Ta có $\int 2^{x} dx = \frac{2^{x}}{\ln 2} + C$

Câu 21:

Cho hai hàm số f(x) và g(x) xác định và liên tục trên R. Tìm khẳng định sai?

A.

[\int f (x) . g (x)] dx = \int f (x) dx . \int g (x) dx

B.

\int k . f (x) dx = k \int f (x) dx

C.

\int f' (x) dx = f (x) + C

D.

\int [f (x) + g (x)] dx = \int f (x) dx + \int g (x) dx

Xem đáp án

Đáp án đúng là: A

Đáp án A sai do không có công thức

[\int f (x) . g (x)] dx = \int f (x) dx . \int g (x) dx

Câu 22:

Trong không gian Oxyz, mặt phẳng qua hai điểm A(1; 1; 2); B(2; 1; −1) và vuông góc với mặt phẳng (α) : 2x – 2y + z – 1 = 0 có phương trình là:

A. 6x + 7y – 2z + 17 = 0

B. 6x – 7y + 2z + 17 = 0

C. 6x + 7y + 2z – 17 = 0

D. 6x + 7y + 2z + 17 = 0

Xem đáp án

Đáp án đúng là: C

Gọi $\vec{u}$ là $\vec{AB}$ có tọa độ (1; 0; −3).

Gọi $\vec{v}$ là vectơ pháp tuyến của (α) là: $\vec{v}$ = (2; −2; 1).

Vectơ pháp tuyến của mặt phẳng là $[\vec{u} . \vec{v}]$ = (−6; −7; −2) = (6; 7; 2).

Phương trình mặt phẳng đi qua A(1; 1; 2) có vectơ pháp tuyến là (6; 7; 2) là:

6(x −1) + 7(y – 1) + 2(z – 2) = 0

Û 6x + 7y + 2z – 6 – 7 – 4 = 0

Û 6x + 7y + 2z − 17 = 0.

Câu 23:

Trong không gian Oxyz, cho mặt cầu (S) : (x – 1)² + (y – 2)² + (z – 3)² = 4. Tâm và bán kính của mặt cầu đã cho là:

A. I(−1; −2; −3) và R = 2

B. I(1; 2; 3) và R = 4

C. I(−1; −2; −3) và R = 16

D. I(1; 2; 3) và R = 2

Xem đáp án

Đáp án đúng là: D

Mặt cầu (S) : (x – 1)² + (y – 2)² + (z – 3)² = 4 có tâm I(1; 2; 3) và R = $\sqrt{4}$ = 2

Câu 24:

Mặt cầu tâm I(1; 2; 3) và bán kính R = 2 có phương trình là:

A. (x – 1)² + (y – 2)² + (z – 3)² = 4

B. (x – 1)² + (y – 2)² + (z – 3)² = 2

C. (x + 1)² + (y + 2)² + (z + 3)² = 2

D. (x + 1)² + (y + 2)² + (z + 3)² = 4

Xem đáp án

Đáp án đúng là: A

Mặt cầu tâm I(1; 2; 3) và bán kính R = 2 có phương trình là:

(x – 1)² + (y – 2)² + (z + 3)² = 4.

Câu 25:

Cho hàm số f(x) liên tục tren R. Gọi V là thể tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = −1 và x = 4 (như hình vẽ bên) khi quay quanh trục Ox. Mệnh đề nào sau đây sai?

Cho hàm số f(x) liên tục tren R. Gọi V là thể tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = −1 và x = 4 (ảnh 1)

A. V = $π (\int_{- 1}^{1} f^{2} (x) dx - \int_{1}^{4} f^{2} (x) dx)$

B. V = $\int_{- 1}^{4} {πf}^{2} (x) dx$

C. V = $π \int_{- 1}^{4} f^{2} (x) dx$

D. V = $π (\int_{- 1}^{1} f^{2} (x) dx + \int_{1}^{4} f^{2} (x) dx)$

Xem đáp án

Đáp án đúng là: A

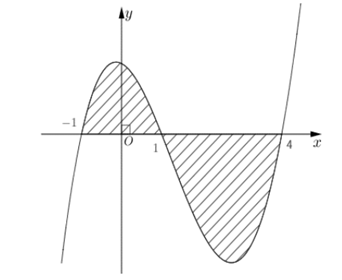
Ta có: hàm số f(x) ≥ 0 ∀ x ∈ [−1; 1]; f(x) ≤ 0 ∀ x ∈ [1; 4], nên ta có:

$V = π \int_{- 1}^{4} f^{2} (x) dx = π (\int_{1}^{4} f^{2} (x) dx + \int_{- 1}^{1} f^{2} (x) dx)$

Vậy thể tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = −1 và x = 4 là:

$V = π (\int_{1}^{4} f^{2} (x) dx + \int_{- 1}^{1} f^{2} (x) dx)$

Câu 26:

Nguyên hàm của hàm số f(x) = sin2x là:

A. F(x) = sin2x + C

B. F(x) =

\frac{\sin 2 x}{2} + C

C. F(x) = −cos2x + C

D. F(x) =

- \frac{\cos 2 x}{2} + C

Xem đáp án

Đáp án đúng là: D

Ta có

\int \sin 2 xdx = - \frac{\cos 2 x}{2} + C

Câu 27:

Chọn khẳng định đúng?

A.

\int_{a}^{b} f' (x) dx

= f(a) – f(b).

B.

\int_{a}^{b} f' (x) dx

= f(a)− f(b).

C.

\int_{a}^{b} f' (x) dx

= f(b) – f(a).

D.

\int_{a}^{b} f' (x) dx

= f(b) – f(a).

Xem đáp án

Đáp án đúng là: D

Do f '(x) có nguyên hàm là f(x) nên $\int f' (x) dx$ = f(x) + C.

Từ đó ta có:

\int_{a}^{b} f' (x) dx

= f(b) – f(a).

Câu 28:

Tính tích phân

\int_{0}^{1} x (x^{2} + 3) dx

bằng cách đặt ẩn phụ t = x² + 3 thì tích phân trở thành:

A. $\int_{0}^{1} \frac{tdt}{2}$

B. $\int_{3}^{4} \frac{tdt}{2}$

C. $\int_{3}^{4} tdt$

D. $- \int_{0}^{1} tdt$

Xem đáp án

Đáp án đúng là: B

Đặt t = x² + 3 Û dt = 2xdx Þ xdx = $\frac{1}{2}$ dt

Đổi cận :

x	1	0
t	4	3

Do đó:

\int_{0}^{1} x (x^{2} + 3) dx = \int_{3}^{4} \frac{1}{2} tdt

Câu 29:

Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1; 2; −3) và song song với mặt phẳng 2x – y + 3z + 2022 = 0 là:

A. 2x – y + 3z – 4 = 0

B. 2x – y + 3z + 4 = 0

C. 2x – y + 3z + 9 = 0

D. x – 2y – 4 = 0

Xem đáp án

Đáp án đúng là: C

Gọi phương trình cần tìm là (P).

Gọi (Q) là mặt phẳng 2x – y + 3z + 2022.

Do (P) và (Q) song song nên vectơ pháp tuyến của (Q) cũng là vectơ pháp tuyến của (P)

Phương trình (P) đi qua A(1; 2; −3) và có vectơ pháp tuyến (2; −1; 3) là:

2(x – 1) −1(y – 2) + 3(z + 3) = 0

Û 2x – y + 3z – 2 + 2 + 9 = 0

Û 2x – y + 3z + 9 = 0.

Câu 30:

Khoảng cách từ điểm A(1; 1; 3) đến x – 2y + 2z – 1 = 0 là:

A. $\frac{5}{3}$

B. 0

C. $\frac{4}{3}$

D. 1

Xem đáp án

Đáp án đúng là: C

Gọi mặt phẳng (P) có phương trình: 2x – y + 3z + 2022 = 0.

Khi đó, khoảng cách từ điểm A(1; 1; 3) đến x – 2y + 2z – 1 = 0 là:

d_(A;(P)) =

\frac{|1.1 - 2.1 + 2.3 - 1|}{\sqrt{1 + 2^{2} + 2^{2}}} = \frac{4}{3}

.

Câu 31:

Tìm họ nguyên hàm F(x) =

\int x^{2} dx

A. F(x) =

\frac{x^{3}}{3}

+ C

B. F(x) = 2x + C

C. F(x) =

- \frac{x^{3}}{3}

+ C

D. F(x) = x² + C

Xem đáp án

Đáp án đúng là: A

Ta có

\int x^{2} dx = \frac{x^{3}}{3} + C

Câu 32:

Trong không gian Oxyz, cho

\vec{u} = \vec{i} - 2 \vec{j} + 3 \vec{k}

. Vectơ

\vec{u}

có tọa độ:

A. (−1; −2; 3)

B. (3; −2; 1)

C. (−2; 3; 1)

D. (1; −2; 3)

Xem đáp án

Đáp án đúng là: D

Ta có: $\vec{u} = \vec{i} - 2 \vec{j} + 3 \vec{k}$

Khi đó, vectơ $\vec{u}$ có tọa độ là (1; −2; 3).

Câu 33:

Mặt phẳng đi qua M(1; 2; 3) và nhận $\vec{n}$ = (2; −1; 1) làm vectơ pháp tuyến là:

A. 2x – y + z + 3 = 0

B. 2x –y + z – 3 = 0

C. 2x + y + z + 3 = 0

D. 2x – y – z – 3 = 0

Xem đáp án

Đáp án đúng là: B

Mặt phẳng đi qua M(1; 2; 3) và nhận $\vec{n}$ = (2; −1; 1) làm vectơ pháp tuyến là:

2(x – 1) – 1(y – 2) + 1(z – 3) = 0

Û 2x – y + z – 2 + 2 – 3 = 0

Vậy mặt phẳng 2x – y + z – 3 = 0 đi qua M(1; 2; 3) và nhận $\vec{n}$ = (2; −1; 1) làm vectơ pháp tuyến.

Câu 34:

Cho F(x) là một nguyên hàm của hàm số f(x) = e^x , chọn mệnh đề đúng:

A. F(x) = −e^x + C

B. F(x) = e^x + C

C. F(x) =

\frac{e^{x}}{x}

+ C

D. F(x) =

\frac{e^{x}}{2}

+ C

Xem đáp án

Đáp án đúng là: B

Ta có $\int e^{x} dx$ = e^x + C.

Câu 35:

Diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thằng x = a, x = b được tính theo công thức:

A. S = $\int_{a}^{b} |f (x)| dx$

B. S = $\int_{a}^{b} f (x) dx$

C. S = $|\int_{a}^{b} f (x) dx|$

D. S = $\int_{a}^{b} f (|x|) dx$

Xem đáp án

Đáp án đúng là: A

Hàm số y = f(x) liên tục trên đoạn [a; b], trục hoành và hai đường thằng x = a, x = b có công thức tính là: S = $\int_{a}^{b} |f (x)| dx$ .

Câu 36:

Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

A. $\int_{- 1}^{2} (2 x - 2) dx$

B. $\int_{- 1}^{2} (- 2 x + 2) dx$

C. $\int_{- 1}^{2} (- 2 x^{2} + 2 x + 4) dx$

D. $\int_{- 1}^{2} (2 x^{2} - 2 x - 4) dx$

Xem đáp án

Đáp án đúng là: C

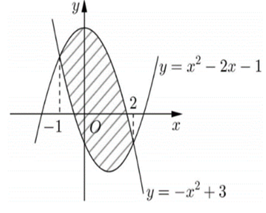
Phương trình trục hoành là:

x² – 2x −1 = −x² + 3

Û −x² + 3 – x² + 2x + 1 = 0

Û −2x² + 2x + 4 = 0

Û $[\begin{matrix} x = 2 \\ x = - 1 \end{matrix}$

Diện tích hình phẳng giới hạn bởi y = x² – 2x – 1 và y = −x² + 3 là:

S = $\int_{- 1}^{2} (- 2 x^{2} + 2 x + 4) dx$

Câu 37:

Cho hình phẳng (α) : 2x – 3y – 4z + 1 = 0. Khi đó, một vectơ pháp tuyến của (α)

A.

\vec{n}

= (2; −3; −4)

B.

\vec{n}

= (−2; 3; 1)

C.

\vec{n}

= (2; 3; −4)

D.

\vec{n}

= (2; −3; 4)

Xem đáp án

Đáp án đúng là: A

Hình phẳng (α) : 2x – 3x – 4z + 1 = 0 có vectơ pháp tuyến là:

\vec{n}

= (2; −3; −4).

Câu 38:

Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và x = a, x = b là:

A. V = $\int_{a}^{b} |f (x)| dx$

B. V = $π \int_{a}^{b} f (x) dx$

C. V = $π \int_{a}^{b} |f (x)| dx$

D. V = $π \int_{a}^{b} f^{2} (x) dx$

Xem đáp án

Đáp án đúng là: D

Vì V là thể tích vật thể tròn xoay nhận được khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và x = a, x = b là:

V = $π \int_{a}^{b} f^{2} (x) dx$

Câu 39:

Tích phân I =

\int_{0}^{2} 2 xdx

. Khẳng định nào sau đây đúng?

A. I = $\int_{0}^{2} 2 xdx = {4 x^{2}|}_{0}^{2}$

B. I = $\int_{0}^{2} 2 xdx = {x^{2}|}_{2}^{0}$

C. I = $\int_{0}^{2} 2 xdx = {2|}_{0}^{2}$

D. I = $\int_{0}^{2} 2 x dx= {x^{2}|}_{0}^{2}$

Xem đáp án

Đáp án đúng là: D

Ta có $\int_{0}^{2} 2 xdx = {x^{2}|}_{0}^{2}$

Do đó khẳng định D đúng.

Câu 40:

Cho đường thẳng y =

\frac{3}{4}

x và parabol y =

\frac{1}{2}

x² + a, (a là tham số thực dương). Gọi S₁, S₂ lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi S₁ = S₂ thì a thuộc khoảng nào dưới đây?

Cho đường thẳng y = 3/4x và parabol y = 1/2x^2 + a, (a là tham số thực dương). (ảnh 1)

A. $(0; \frac{3}{16})$

B. $(\frac{3}{16}; \frac{7}{32})$

C. $(\frac{1}{4}; \frac{9}{32})$

D. $(\frac{7}{32}; \frac{1}{4})$

Xem đáp án

Đáp án đúng là: B

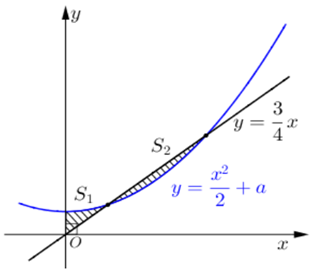
Phương trình hoành độ giao điểm của hai đồ thị là

$\frac{3}{4}$ x = $\frac{1}{2}$ x² + a Û 2x² – 3x + 4a = 0 (*)

Ta có: (d) cắt (P) tại 2 điểm phân biệt có hoành độ dương nên phương trình có 2 nghiệm dương phân biệt nên:

$\{\begin{matrix} Δ > 0 \\ S > 0 \\ P > 0 \end{matrix}$ Û $\{\begin{matrix} 9 a - 32 a > 0 \\ 2 a > 0 \end{matrix}$

Û 0 < a < $\frac{9}{32}$ .

Gọi F(x) là một nguyên hàm của hàm số f(x) = $\frac{1}{2}$ x² − $\frac{3}{4}$ x + a.

Khi đó:

S₁ = $\int_{0}^{x_{1}} (\frac{1}{2} x^{2} - \frac{3}{4} x + a) dx$

= ${\frac{1}{6} x^{3} - \frac{3}{8} x^{2} +ax|}_{0}^{x_{1}}$ = F(x₁).

S₂ = $\int_{x_{1}}^{x_{2}} (- \frac{1}{2} x^{2} + \frac{3}{4} x - a) dx$

= ${- F (x)|}_{x_{1}}^{x_{2}}$ = −F(x₂) + F(x₁).

Ta có: S₁= S₂ Û F(x₂) = 0

Û $\frac{1}{6} x_{2}^{3} - \frac{3}{8} x_{2}^{2}$ + ax₂ = 0

Û $4 x_{2}^{2}$ − 9x₂ + 24a = 0

Do x₂ là nghiệm của phương trình (*) nên ta có hệ phương trình:

$\{\begin{matrix} 2 x_{2}^{2} - 3 x_{2} + 4 a = 0 \\ 4 x_{2}^{2} - 9 x_{2} + 24 a = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} 2 x_{2}^{2} - 3 x_{2} + 4 a = 0 \\ 16 a - 3 x_{2} = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} 2 . \frac{256}{9} a^{2} - 16 a + 4 a = 0 \\ x_{2} = \frac{16 a}{3} \end{matrix} \Rightarrow \frac{512}{9} a^{2} - 12 a = 0 \Leftrightarrow [\begin{matrix} a = 0 \\ a = \frac{27}{128} \end{matrix}$

Đối chiếu điều kiện của a nên ta có $a = \frac{27}{128} \in (\frac{3}{16}; \frac{7}{12})$

Câu 41:

Cho f(x) là hàm số liên tục trên ℝ thỏa mãn f(1) = 1 và

\int_{0}^{1} f (t) dt = \frac{1}{3}

, tính

I = \int_{0}^{\frac{π}{2}} \sin 2 x . f' (sinx) dx

.

A. I = $\frac{2}{3}$

B. I = $\frac{1}{3}$

C. I = $\frac{4}{3}$

D. I = $- \frac{2}{3}$

Xem đáp án

Đáp án đúng là: C

Đặt t = sinx Û dt = cosxdx

Đổi cận :

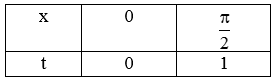
Cho f(x) là hàm số liên tục trên ℝ thỏa mãn f(1) = 1 và tích phân từ 0 đến 1 f(t)dt = 1/3 (ảnh 1)

Khi đó: I = $\int_{0}^{\frac{π}{2}} \sin 2 xdx . f' (sinx) dx$

$= \int_{0}^{\frac{π}{2}} 2 sinx . cosx . f' (sinx) dx = 2 . \int_{0}^{1} t . f' (t) dt$

Đặt $\{\begin{matrix} u = t \\ dv = f' (t) dt \end{matrix} \Leftrightarrow \{\begin{matrix} du = dt \\ v = f (t) \end{matrix}$

Do đó:

I = 2 - [{(t . f (t))|}_{0}^{1} - \int_{0}^{1} f (t) dt] = 2 (1 - \frac{1}{3}) = \frac{4}{3}

Câu 42:

Một cốc thủy tinh có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc là một đường Parabol. Tính thể tích tối đa mà cốc có thể chứa được:

Một cốc thủy tinh có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc là một đường Parabol. (ảnh 1)

A. V » 251,33 cm³

B. V » 502,65 cm³

C. V » 100,53 cm³

D. V » 320 cm³

Xem đáp án

Đáp án đúng là: A

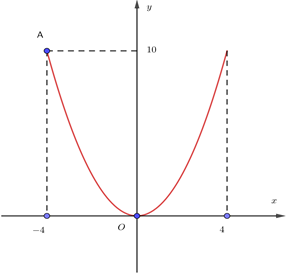
Một cốc thủy tinh có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc là một đường Parabol. (ảnh 2)

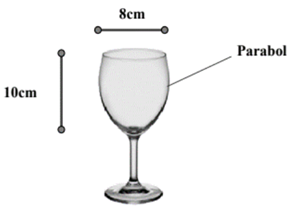
Parabol có dạng y = ax² (P)

(P) đi qua A (−4; 10), ta có:

10 = a. 4² Û a = $\frac{10}{16}$ hay a = $\frac{5}{8}$

Nên y = $\frac{5}{8}$ x² hay x² = $\frac{8}{5}$ y

Thể tích khi quay (P) quanh Oy là:

V =

π \int_{0}^{10} \frac{8}{5} ydy

= 80π » 251,2 (cm³).

Câu 43:

Cho hàm số f(x) liên tục trên đoạn [0; 1] và

\int_{0}^{\frac{π}{2}} f (s inx) dx

= 5. Tính

I = \int_{0}^{π} xf (s inx) dx

A. I = 10π

B. I =

\frac{5}{2}

π

C. 5π

D. 5

Xem đáp án

Đáp án đúng là: C

Với I₁ = $\int_{0}^{\frac{π}{2}} f (s inx) dx$ .

Đặt x = $\frac{π}{2}$ − t Û dx = −dt

Đổi cận :

Cho hàm số f(x) liên tục trên đoạn [0; 1] và tích phân từ 0 đến pi/2 f(sinx)dx = 5. Tính (ảnh 1)

Do đó: I₁ = $\int_{\frac{π}{2}}^{0} f (\sin (\frac{π}{2} - t)) dt$ = $\int_{0}^{\frac{π}{2}} f (cost) dt$ .

Từ đó suy ra được: f(sinx) = f(cosx)

$\int_{0}^{π} x . f (s inx) dx$ = $\int_{0}^{\frac{π}{2}} x . f (s inx) dx + \int_{\frac{π}{2}}^{π} x . f (s inx) dx$

Đổi biến u = $\frac{π}{2}$ − x

Nên I₂ = $\int_{0}^{\frac{π}{2}} (\frac{π}{2} - u) . f (cosu) du$ = $\int_{0}^{\frac{π}{2}} (\frac{π}{2} - x) . f (s inx) dx$ .

Do đó: 2I₂ = $\int_{0}^{\frac{π}{2}} \frac{π}{2} . f (s inx) dx$ Þ I₂ = $\frac{π}{4} . \int_{0}^{\frac{π}{2}} f (s inx) dx$ .

Với $\int_{0}^{\frac{π}{2}} f (s inx) dx = 5$

Đặt t = π – x.

Suy ra I₁= $\int_{\frac{π}{2}}^{π} f (\sin (π - t)) dt$ = $\int_{\frac{π}{2}}^{π} f (- sint) dt$ .

Đổi biến: v = $\frac{3 π}{2}$ − t

Suy ra I₁ =

\int_{\frac{π}{2}}^{π} f [- \sin (\frac{3 π}{2} - v)] dv

=

\int_{\frac{π}{2}}^{π} f (cosv) dv

Trên $(\frac{π}{2}; π)$ thì sinx = −cosx, ta có:

I₃ = $\int_{\frac{π}{2}}^{π} x . f (s inx) dx$ .

Đổi biến : u = $\frac{3 π}{2}$ − x, ta được:

I₃ = $\int_{\frac{π}{2}}^{π} [(\frac{3 π}{2} - u) . f (\sin (\frac{3 π}{2} - u))] du$

= $\int_{\frac{π}{2}}^{π} (\frac{3 π}{2} - u) . f (- cosu) du$

Từ đó, ta có: 2I₃ = $\int_{\frac{π}{2}}^{π} \frac{3 π}{2} . f (- s inx) dx$

Þ I₃ = $\int_{\frac{π}{2}}^{π} \frac{3 π}{4} . f (- s inx) dx$

Þ I = I₂ + I₃ = π. $\int_{π}^{\frac{π}{2}} f (x) dx$ = 5π.

Vậy I = $\int_{0}^{π} xf (s inx) dx$ = 5π.

Câu 44:

Phương trình x² + y² + z² + 2x – 2z + m – 5 = 0 là phương trình một mặt cầu, khi đó diện tích xung quanh của khối cầu đó là:

A. S = 4π(7 – m)

B. S = π(7 – m)

C. S = 16π(m – 7)

D. S = 4π(m – 7)

Xem đáp án

Đáp án đúng là: A

Ta có: x² + y² + z² + 2x – 2z + m – 5 = 0

Û (x + 1)² – 1 + y² + (z − 1)² – 1 + m – 5 = 0

Û (x + 1)² + y² + (z – 1)² = 7 – m

Suy ra R² = 7 – m.

Do đó S_xq = 4πR² = 4π.(7 – m).

Câu 45:

Biết

\int (x + 3) . e^{- 2 x} dx = - \frac{1}{m} e^{- 2 x} (2 x + n) + C

, với m, n Î ℚ. Khi đó tổng S = m² + n² có giá trị bằng

A. 10

B. 65

C. 41

D. 5

Xem đáp án

Đáp án đúng là: B

Đặt: $\{\begin{matrix} u = x + 3 \\ dv = e^{- 2 x} dx \end{matrix} \Leftrightarrow \{\begin{matrix} du = dx \\ v = - \frac{1}{2} e^{- 2 x} \end{matrix}$

Do đó: $\int (x + 3) . e^{- 2 x} dx = - \frac{1}{2} e^{- 2 x} (x + 3) + \frac{1}{2} \int e^{- 2 x} dx$

$= - \frac{1}{2} . e^{- 2 x} (x + 3) - \frac{1}{4} e^{- 2 x} + C = - \frac{1}{4} e^{- 2 x} . (2 x + 6 + 1) + C = - \frac{1}{4} e^{- 2 x} (2 x + 7) + C$

Do đó m = 4, n = 7.

Vậy S = m² + n² = 4²+ 7² = 65.

Câu 46:

Trong không gian Oxyz, cho hai điểm A(1; 2;1); B(2; −1; 3) và điểm M(a; b; 0) sao cho MA² + MB² nhỏ nhất. Giá trị của a + b là:

A. -2

B. 2

C. 1

D. 3

Xem đáp án

Đáp án đúng là: B

Ta có: MA² + MB² = (a – 1)² + (b – 2)² + 1² +(a – 2)² + (b + 1)²+ 3²

= 2a² + 2b² – 6a – 2b + 10 = 2(a² + b² – 3a – b + 5)

= 2 $[{(a - \frac{3}{2})}^{2} + {(b - \frac{1}{2})}^{2} + \frac{5}{2}]$ ≥ $\frac{5}{2}$

Dấu “ = ” xảy ra khi và chỉ khi : a = $\frac{3}{2}$ , b = $\frac{1}{2}$ .

Vậy a + b = $\frac{3}{2} + \frac{1}{2}$ = 2.

Câu 47:

Trong không gian Oxyz, cho mặt phẳng (P) : x + 2y – 2z + 3 = 0 và mặt cầu (S) có tâm I(0; −2; 1). Biết mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có diện tích 2π. Mặt cầu (S) có phương trình là

A. x² + (y + 2)² + (z + 1)² = 3

B. x² + (y + 2)² + (z + 1)² = 1

C. x² + (y + 2)² + (z – 1)² = 3

D. x² + (y + 2)² + (z + 1)² = 2

Xem đáp án

Đáp án đúng là: C

Gọi R, r lần lượt là bán kính của mặt cầu và đường tròn giao tuyến.

Theo giả thiết ta có: πr² = 2π Û r² = 2 Û r = $\sqrt{2}$ .

Khi đó: d_(I,(P)) = $\frac{|0 + 2. (- 2) - 2.1 + 3|}{\sqrt{1^{2} + 2^{2} + 2^{2}}}$ = 1.

Mặt khác: d_{(I; (P))} = 1

Suy ra R² = r² + ${[d_{(I, (P))}]}^{2}$ = ${(\sqrt{2})}^{2} + 1^{^{2}}$ = 3.

Vậy phương trình mặt cầu là: x² + (y + 2)² + (z – 1)² = 3.

Câu 48:

Trong không gian với hệ tọa độ Oxyz, cho điểm M (3; 2; 1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC . Trong các mặt phẳng sau, tìm mặt phẳng vuông góc với mặt phẳng (P) .

A. 4x – 2y + z − 10 = 0

B. 3x + 2y + z + 10 = 0

C. 2x – 2y + z + 9 = 0

D. x – 2y + z − 10 = 0

Xem đáp án

Đáp án đúng là: D

Gọi A(a; 0; 0), B(0; b; 0), C(0; 0; c)

Phương trình mặt phẳng (P) có dạng: $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ (với a, b, c ≠ 0)

Vì (P) qua M nên : $\frac{3}{a} + \frac{2}{b} + \frac{1}{c} = 1$ (1)

Ta có: $\vec{MA}$ = (a – 3, – 2, – 1); $\vec{MB}$ = (−3, b – 2, −1);

$\vec{BC}$ = (0; −b; c); $\vec{AC}$ = (−a; 0; c).

Vì M là trực tâm tam giác ABC nên :

$\{\begin{matrix} \vec{MA} . \vec{BC} = 0 \\ \vec{MB} . \vec{AC} = 0 \end{matrix}$ Þ $\{\begin{matrix} 2 b = c \\ 3 a = c \end{matrix}$ (2)

Từ (1) và (2) ta được: a = $\frac{14}{3}$ ; b = $\frac{14}{2}$ ; c = 14.

Khi đó phương trình (P): 3x + 2y + z – 14 = 0 có vectơ pháp tuyến là $\vec{u}$ = (3; 2; 1).

Gọi (Q) là mặt phẳng vuông góc với mặt phẳng (P).

Mặt phẳng (P) ^ (Q) nên $\vec{n_{(P)}}$ ^ $\vec{n_{(Q)}}$ .

Lấy đáp án D có $\vec{n_{(Q)}}$ = (1; −2; 1).

Suy ra $\vec{n_{(P)}} . \vec{n_{(Q)}}$ = (1; −2; 1) . (3; 2; 1) = 3 – 4 + 1 = 0.

Vậy phương trình mặt phẳng (Q) có dạng x – 2y + z – 10 = 0.

Câu 49:

Cho hàm số y = f(x) liên tục trên [0; +∞) và

\int_{0}^{3} f (\sqrt{x + 1}) dx

= 8. Tính tích phân I =

\int_{1}^{2} xf (x) dx

A. I = 8

B. I = 2

C. I = 16

D. I = 4

Xem đáp án

Đáp án đúng là: D

Ta có $\int_{0}^{3} f (\sqrt{x + 1}) dx = 8$

Đặt u = $\sqrt{x + 1}$ Û u² = x + 1 Û 2udu = dx.

Đổi cận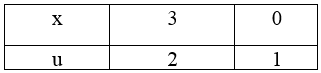

Cho hàm số y = f(x) liên tục trên [0; +∞) và tích phân từ 0 đến 8 f(căn bậc hai x+1)dx = 8. (ảnh 1)

Do đó ta được: $\int_{1}^{2} f (u) 2 udu = 8$

Û $2 \int_{1}^{2} f (u) udu = 8$ Þ $\int_{1}^{2} uf (u) du = 4$

Do đó $\int_{1}^{2} xf (x) dx = 4$ .

Câu 50:

Cho hàm số y = f (x) thỏa mãn f (x) < 0, ∀ x > 0 và có đạo hàm f '(x) liên tục trên khoảng (0; +∞) thỏa mãn f '(x) = (2x +1)f²(x), ∀ x >0 và f(1) =

- \frac{1}{2}

. Giá trị của biểu thức f(1) + f(2) + ... + f(2022) bằng

A. $- \frac{2022}{2021}$

B. $- \frac{2022}{2023}$

C. $- \frac{2019}{2020}$

D. $- \frac{2021}{2022}$

Xem đáp án

Đáp án đúng là: B

Ta có: f '(x) = (2x + 1).f ²(x) nên $\frac{f' (x)}{f^{2} (x)} = 2 x + 1$

Û ${(- \frac{1}{f (x)})}^{'} = 2 x + 1$

Û $- \frac{1}{f (x)} = \int (2 x + 1) dx$

Û $- \frac{1}{f (x)}$ = x² + x + C

Cho x = 1, ta có:

$- \frac{1}{f (1)} = 1^{2} + 1 + C$

Û $- \frac{1}{f (1)}$ = 2 + C

Û 2 = 2 + C Û C = 0.

Do đó: $- \frac{1}{f (x)}$ = x² + x

Û f(x) = $- \frac{1}{x^{2} + x}$

Û f(x) = $- \frac{1}{x (x + 1)} = \frac{1}{x + 1} - \frac{1}{x}$ .

Từ đó ta có:

f(1) = $\frac{1}{1 + 1} - \frac{1}{1}$ = $\frac{1}{2} - 1$ ;

f(2) = $\frac{1}{3} - \frac{1}{2}$ .

Tương tự như vậy:

f(2022) = $\frac{1}{2023} - \frac{1}{2022}$

Vậy f(1) + f(2) + ... + f(2022) = $\frac{1}{2023} - \frac{1}{1}$ = $- \frac{2022}{2023}$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất)

Đề kiểm tra Giữa học kì 2 Toán 12 có đáp án (Mới nhất) (Đề 10)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương