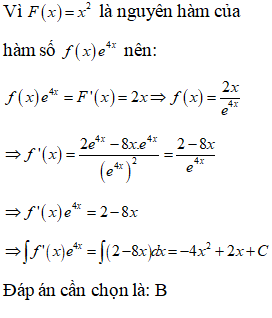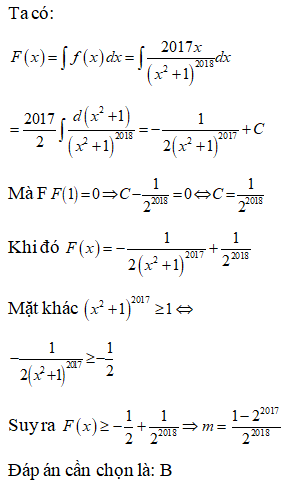15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Nguyên hàm có đáp án (Vận dụng)

Câu 1:

Cho $I = \int \frac{d x}{\sqrt{2 x - 1} + 4} = \sqrt{2 x - 1} - \ln {(\sqrt{2 x - 1} + 4)}^{n} + C$ ở đó $n \in N *$ . Giá trị biểu thức $S = \sin \frac{n π}{8}$ là:

A. $\frac{1}{2}$

B. 0

C.1

D. -1

Xem đáp án

Câu 2:

Cho hàm số $f (x) = \frac{1}{\sin^{2} x}$ . Nếu $F (x)$ là một nguyên hàm của hàm số $f (x)$ và đồ thị hàm số $y = F (x)$ đi qua $M (\frac{π}{3}; 0)$ thì là:

A. $F (x) = \frac{1}{\sqrt{3}} - \cot x$

B. $F (x) = \sqrt{3} - \cot x$

C. $F (x) = \frac{\sqrt{3}}{2} - \cot x$

D. $F (x) = - \cot x + C$

Xem đáp án

Ta có: $\int f (x) d x = \int \frac{1}{\sin^{2} x} d x = - \cot x + C = F (x)$

Đồ thị hàm số $y = F (x)$ đi qua $M (\frac{π}{3}; 0)$ nên $F (\frac{π}{3}) = 0$ $\Leftrightarrow - \cot \frac{π}{3} + C = 0 \Leftrightarrow C = \frac{1}{\sqrt{3}} \Rightarrow$ $F (x) = \frac{1}{\sqrt{3}} - \cot x$

Đáp án cần chọn là: A

Câu 3:

Cho $F (x)$ là một nguyên hàm của hàm số $f (x) = |1 + x| - |1 - x|$ trên tập R và thỏa mãn $F (1) = 3; F (- 1) = 2; F (- 2) = 4$ . Tính tổng $T = F (0) + F (2) + F (- 3)$

A. 8

B.12

C. 14

D.10

Xem đáp án

Ta có: $f (x) = |1 + x| - |1 - x|$

theo đề bài ta có: $\{\begin{matrix} F (1) = 3 \\ F (- 1) = 2 \\ F (- 2) = 4 \end{matrix} \Leftrightarrow \{\begin{matrix} 2 + C_{1} = 3 \\ 1 + C_{2} = 2 \\ 4 + C_{3} = 4 \end{matrix} \Leftrightarrow \{\begin{matrix} C_{1} = 1 \\ C_{2} = 1 \\ C_{3} = 0 \end{matrix}$

$\Rightarrow F (x) = \{\begin{matrix} 2 x + 1 k h i x \geq 1 \\ x^{2} + 1 k h i - 1 \leq x < 1 \\ - 2 x k h i x < - 1 \end{matrix}$ $\Rightarrow \{\begin{matrix} F (2) = 2.2 + 1 = 5 \\ F (0) = 1 \\ F (- 3) = - 2. (- 3) = 6 \end{matrix}$ $\Rightarrow T = 5 + 1 + 6 = 12$

Đáp án cần chọn là: B

Câu 4:

Cho $F (x)$ là một nguyên hàm của hàm số $f (x) = x . \sqrt{x^{2} - m}$ . Số giá trị của tham số m để $F (\sqrt{2}) = \frac{7}{3}$ và $F (\sqrt{5}) = \frac{14}{3}$ là:

A.3

B. 4

C.1

D.2

Xem đáp án

ta có $F (x) = \int f (x) d x = \int x . \sqrt{x^{2} - m} d x$ . Đặt $t = \sqrt{x^{2} - m} \Rightarrow t^{2} = x^{2} - m \Leftrightarrow t d x = x d x$ $\Rightarrow F (x) = \int t . t d t = \int t^{2} d t = \frac{t^{3}}{3} + C = \frac{{(\sqrt{x^{2} - m})}^{3}}{3} + C$

Theo bài ra ta có: $\{\begin{cases} F (\sqrt{2}) = \frac{7}{3} \\ F (\sqrt{5}) = \frac{14}{3} \end{cases} \Leftrightarrow \{\begin{cases} \frac{{(\sqrt{2 - m})}^{3}}{3} + C = \frac{7}{3} \\ \frac{{(\sqrt{5 - m})}^{3}}{3} + C = \frac{14}{3} \end{cases}$ $\Leftrightarrow \{\begin{cases} \frac{{(\sqrt{2 - m})}^{3}}{3} + C = \frac{7}{3} \\ \frac{{(\sqrt{5 - m})}^{3}}{3} - \frac{{(\sqrt{2 - m})}^{3}}{3} = \frac{7}{3} \end{cases} \Leftrightarrow \{\begin{cases} \frac{{(\sqrt{2 - m})}^{3}}{3} + c = \frac{7}{3} \\ {(\sqrt{5 - m})}^{3} - {(\sqrt{2 - m})}^{3} - 7 = 0 \end{cases}$

xét hàm số: $f (m) = {(\sqrt{5 - m})}^{3} - {(\sqrt{2 - m})}^{3} - 7 (m \leq 2)$

Ta có: $f' (m) = - \frac{3}{2} \sqrt{5 - m} + \frac{3}{2} (\sqrt{2 - m} - \sqrt{5 - m})$ . Vì $2 - m < 5 - m \forall m \leq 2 \Rightarrow \sqrt{2 - m} < \sqrt{5 - m} \forall m \leq 2$ .Do đó, $f' (m) < 0 \forall m \leq 2$

Suy ra hàm số f(m) nghịch biến trên $(- \infty, 2)$

Khi đó phương trình (*)

có nhiều nhất 1 nghiệm, mà $f (1)$ = 0

nên m = 1 là nghiệm duy nhất

của phương trình (*)

Vậy có 1 giá trị của m thỏa

mãn yêu cầu bài toán

Đáp án cần chọn là: C

Câu 5:

Cho hàm số $y = f (x)$ có $f' (x) = \frac{1}{x + 1}$ . Biết rằng $f (0) = 2018$ . Giá trị của biểu thức $f (3) - f (1)$ bằng:

A. ln2

B. 2ln4

C. ln3

D. 2ln2

Xem đáp án

$f (x) = \int f' (x) d x = \int \frac{1}{x + 1} d x = \ln |x + 1| + C$

$f (0) = 2018$ $\Leftrightarrow C = 2018 \Rightarrow f (x) = \ln |x + 1| + 2018$

$\Rightarrow$ $f (3) - f (1)$ $= \ln 4 + 2018 - \ln 2 - 2018 = \ln 2$

Đáp án cần chọn là: A

Câu 6:

Cho hàm số $f (x) = 2 x + e^{x}$ . Tìm một nguyên hàm $F (x)$ của hàm số $f (x)$ thỏa mãn $F (0) = 2019$

A. $F (x) = e^{x} - 2019$

B. $F (x) = x^{2} + e^{x} - 2018$

C. $F (x) = x^{2} + e^{x} + 2017$

D. $F (x) = x^{2} + e^{x} + 2018$

Xem đáp án

Ta có: $F (x) = \int (2 x + e^{x}) d x = x^{2} + e^{x} + C$

do $F (0) = 2019$ nên $0^{2} + e^{0} + C = 2019 \Leftrightarrow C = 2018$

Vậy $F (x) = x^{2} + e^{x} + 2018$

Đáp án cần chọn là: D

Câu 7:

Cho hàm số $F (x) = x^{2}$ là một nguyên hàm của hàm số $f (x) e^{4 x}$ , hàm số $f (x)$ có đạo hàm $f' (x)$ . Họ nguyên hàm của hàm số $f' (x) e^{4 x}$ là:

A. $- 4 x^{2} + 3 x + C$

B. $- 4 x^{2} + 2 x + C$

C. $4 x^{2} + 2 x + C$

D. $- 4 x^{2} + x + C$

Xem đáp án

Câu 8:

Giả sử $F (x) = (a x^{2} + b x + c) e^{x}$ là một nguyên hàm của hàm số $f (x) = x^{2} e^{x}$ . Tính tích $p = a b c$

A. $p = - 4$

B. $p = 1$

C. $p = - 5$

D. $p = - 3$

Xem đáp án

Vì $F (x)$ là một nguyên hàm của hàm số $f (x)$ nên ta có

$F' (x) = (2 a x + b) e^{x} + (a x^{2} + b x + c) e^{x}$

$\begin{array}{l} = (a x^{2} + b x + c + 2 a x + b) e^{x} \\ = [a x^{2} + (2 a + b) x + b + c] e^{x} \end{array}$

Đồng nhất hệ số ta có: $\{\begin{matrix} a = 1 \\ 2 a + b = 0 \\ b + c = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} a = 1 \\ b = - 2 \\ c = 2 \end{matrix}$

Vậy $P = a b c = 1. (- 2) .2 = - 4$

Đáp án cần chọn là: A

Câu 9:

Một đám vi trùng tại ngày thứ t có số lượng $N (t)$ , biết rằng $N' (t) = \frac{4000}{1 + 0, 5 t}$ và lúc đầu đám vi trùng có 250000 con. Hỏi sau 10 ngày số lượng vi trùng (lấy theo phần nguyên) là bao nhiêu?

A. 264334 con

B. 256334 con

C. 300560 con

D. 614678 con

Xem đáp án

Ta có: $N (t) = \int N' (t) d t = \int \frac{4000}{0, 5 t + 1} d t$ $= \frac{4000}{0, 5} \ln |0, 5 t + 1| + C = 8000 \ln |0, 5 t + 1| + C$

Với $t = 0$ thì $250000 = 8000 \ln 1 + C \Leftrightarrow C = 250000$

Vậy $N (t) = 8000 \ln |0, 5 t + 1| + 250000 \Rightarrow N (10) \approx 264334$

Đáp án cần chọn là: A

Câu 10:

Cho hàm số $f (x)$ thỏa mãn $f' (x) . {[f (x)]}^{2018} = x . e^{x} \forall x \in R$ và $f (1) = 1$ . Hỏi phương trình $f (x) = - \frac{1}{e}$ có bao nhiêu nghiệm?

A. 0

B.1

C.3

D. 2

Xem đáp án

Câu 11:

Cho hàm số $f (x)$ xác định trên R\ $\{- 2; 1\}$ thỏa mãn $f' (x) = \frac{1}{x^{2} + x - 2}$ ; $f (0) = \frac{1}{3}$ và $f (- 3) - f (3) = 0$ . Tính giá trị của biểu thức $T = f (- 4) + f (- 1) - f (4)$

A. $\frac{1}{3} \ln 2 + \frac{1}{3}$

B. $\ln 80 + 1$

C. $\frac{1}{3} \ln (\frac{4}{5}) + \ln 2 + 1$

D. $\frac{1}{3} \ln (\frac{8}{5}) + 1$

Xem đáp án

Ta có: $f' (x) = \frac{1}{x^{2} + x - 2}$ $\Rightarrow f (x) = \int f' (x) d x = \int \frac{d x}{x^{2} + x - 2} = \frac{1}{3} \ln |\frac{x - 1}{x + 2}| + C$

Khi đó, $f (x) = \{\begin{matrix} \frac{1}{3} \ln \frac{x - 1}{x + 2} + C_{1} k h i x > 1 \\ \frac{1}{3} \ln \frac{x - 1}{x + 2} + C_{2} k h i x < - 2 \\ \frac{1}{3} \ln \frac{1 - x}{x + 2} + C_{3} k h i - 2 < x < 1 \end{matrix}$

Mà $f (0) = \frac{1}{3}$ $\begin{array}{l} \Rightarrow C_{3} + \frac{1}{3} \ln \frac{1}{2} = \frac{1}{3} \\ \Rightarrow C_{3} = \frac{1}{3} - \frac{1}{3} \ln \frac{1}{2} \end{array}$ và $f (- 3) - f (3) = 0$ $\Leftrightarrow \frac{1}{3} \ln 4 + C_{2} - \frac{1}{3} \ln \frac{2}{5} - C_{1} = 0 \Leftrightarrow C_{2} - C_{1} = - \frac{1}{3} \ln 4 + \frac{1}{3} \ln \frac{2}{5}$

Do đó, $T = \frac{1}{3} \ln \frac{5}{2} + C_{2} + \frac{1}{3} \ln 2 + C_{3} - \frac{1}{3} \ln \frac{1}{2} - C_{1}$

$T = \frac{1}{3} \ln \frac{5}{2} + \frac{1}{3} \ln 2 - \frac{1}{3} \ln \frac{1}{2} - \frac{1}{3} \ln 4 + \frac{1}{3} \ln \frac{2}{5} + \frac{1}{3} - \frac{1}{3} \ln \frac{1}{2}$

$T = \frac{1}{3} \ln (\frac{\frac{5}{2} .2. \frac{2}{5}}{\frac{1}{2} .4. \frac{1}{2}}) + \frac{1}{3}$ $T = \frac{1}{3} \ln 2 + \frac{1}{3}$

Đáp án cần chọn là: A

Câu 12:

Cho hàm số $f (x)$ thỏa mãn ${(f' (x))}^{2} + f (x) . f'' (x) = 15 x^{4} + 12 x, \forall x \in R$ và $f (0) = f' (0) = 1$ . Giá trị của $f^{2} (1)$ bằng:

A. 4

B. $\frac{9}{2}$

C. 8

D. $\frac{5}{2}$

Xem đáp án

Câu 13:

Cho hàm số $f (x)$ có đạo hàm liên tục trên R và thỏa mãn $f (x) > 0, \forall x \in R$ . Cho biết $f (0) = 1$ và $\frac{f' (x)}{f (x)} = 2 - 2 x$ . Tất cả các giá trị thực của tham số m để phương trình $f (x) = m$ có hai nghiệm thực phân biệt là:

A. $0 < m < e$

B. $1 < m < e$

C. $m > e$

D. $0 < m \leq 1$

Xem đáp án

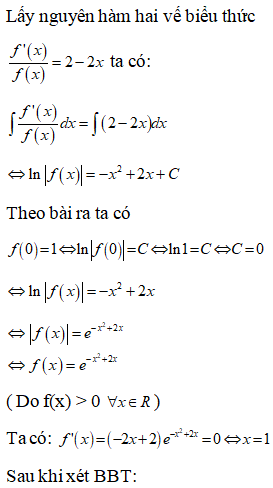
Phương trình f(x) = m có hai nghiệm thực phân biệt khi và chỉ khi đường thẳng

y = m cắt đồ thị hàm số y = f (x) tại hai điểm phân biệt, dựa vào BBT suy ra

0 < m < e

Đáp án cần chọn là: A

Câu 14:

Cho $f (x) = \frac{x^{2}}{\sqrt{1 - x}}$ và $\int f (x) d x = - 2 \int (t^{2} - m) d t$ với $t = \sqrt{1 - x}$ , giá trị của m bằng?

A. $m = 2$

B. $m = - 2$

C. $m = 1$

D. $m = - 1$

Xem đáp án

$f (x) = \frac{x^{2}}{\sqrt{1 - x}}$ và $t = \sqrt{1 - x}$ $\Rightarrow 1 - x = t^{2} \Rightarrow x = 1 - t^{2} \Rightarrow d x = - 2 t d t$

$\Rightarrow \int f (x) d x = \int \frac{{(1 - t^{2})}^{2}}{t} (- 2 t d t)$

$= - 2 \int {(1 - t^{2})}^{2} d t = - 2 \int {(t^{2} - 1)}^{2} d t$ $\Rightarrow m = 1$

Đáp án cần chọn là: C

Câu 15:

Biết $F (x)$ là một nguyên hàm trên R của hàm số $f (x) = \frac{2017 x}{{(x^{2} + 1)}^{2018}}$ thỏa mãn $F (1) = 0$ . Tìm giá trị nhỏ nhất m của $F (x)$

A. $m = - \frac{1}{2}$

B. $m = \frac{1 - 2^{2017}}{2^{2018}}$

C. $m = \frac{2^{2017} + 1}{2^{2018}}$

D. $m = \frac{1}{2}$

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Nguyên hàm có đáp án

Trắc nghiệm Nguyên hàm có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan