30 câu hỏi trắc nghiệm thuộc Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P4)

Câu 1:

Cho hàm số $y = (m - 1) x^{4} - 3 m x^{2} + 5$ . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại mà không có cực tiểu

A. m ∈ (− $\infty$ ;0] ∪ [1;+ $\infty$ )

B. m ∈ [0;1]

C. m ∈ (0;1)

D. m ∈ (− $\infty$ ;0) ∪ (1;+ $\infty$ )

Xem đáp án

Chọn B

[Phương pháp tự luận]

$y^{'} = 4 (m - 1) x^{3} - 6 m x = 0$ (*)

TH1 : Nếu m = 1 , (*) trở thành : $y^{'} = - 6 x = 0$ hay x= 0 , $y^{''} = - 6 < 0$

Vậy m = 1 hàm số đạt cực đại tại x = 0

TH2 : Nếu m ≠ 1

Hàm số có cực đại mà ko có cực tiểu

Kết hợp 2 trường hợp : $m \in [0; 1]$

Câu 2:

Cho hàm số $y = x^{4} - 2 (1 - m^{2}) x^{2} + m + 1$ . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất

A. $m = - \frac{1}{2}$

B. $m = \frac{1}{2}$

C. m = 0

D. m = 1

Xem đáp án

Chọn C

[Phương pháp tự luận]

Hàm số có cực đại , cực tiểu khi và chỉ khi $|m| < 1$

Tọa độ điểm cực trị A $(0; m + 1)$

$(0; m + 1)$

Phương trình đường thẳng BC: $y + m^{4} - 2 m^{2} - m = 0$

Vậy S đạt giá trị lớn nhất $\Leftrightarrow m = 0$

[Phương pháp trắc nghiệm]

Vậy S đạt giá trị lớn nhất $\Leftrightarrow m = 0$

Câu 3:

Tìm các giá trị của tham số m để đồ thị hàm số $y = 2 x^{3} + 3 (m - 3) x^{2} + 11 - 3 m$ có hai điểm cực trị. Đồng thời hai điểm cực trị đó và điểm C(0;-1) thẳng hàng

A. m = 4

B. m = 1

C. m = -3

D. m = 2

Xem đáp án

Chọn A

Phương pháp tự luận]

$y^{'} = 6 x^{2} + 6 (m - 3) x$

Hàm số có 2 cực trị $\Leftrightarrow m \neq 3$

Khi đó đồ thị hàm số đã cho có 2 điểm cực trị A(0;11-3m)

Phương trình đt AB: ${(3 - m)}^{2} x + y - 11 + 3 m = 0$

Câu 4:

Tìm tất cả các giá trị của tham số thực m để đường thẳng qua 2 điểm cực trị của đồ thị hàm số: y = x³ - 3mx +2 cắt đường tròn tâm $I (1; 1)$ bán kính bằng 1 tại 2 điểm $A, B$ mà diện tích tam giác $I A B$ lớn nhất

A. $m = 1 \pm \frac{\sqrt{2}}{2}$

B. $m = 1 \pm \frac{\sqrt{3}}{2}$

C. $m = 1 \pm \frac{\sqrt{5}}{2}$

D. $m = 1 \pm \frac{\sqrt{6}}{2}$

Xem đáp án

Chọn B

[Phương pháp tự luận]

y' = 3x² - 3m

Hàm số có 2 cực trị khi và chỉ khi m > 0

Khi đó tọa độ 2 điểm cực trị của đồ thị hàm số là : $M (\sqrt{m}; - 2 m \sqrt{m} + 2)$

$M (\sqrt{m}; - 2 m \sqrt{m} + 2)$

Phương trình đt MN : $2 m x + y - 2 = 0$ $\Leftrightarrow m = 1 \pm \frac{\sqrt{3}}{2}$

$2 m x + y - 2 = 0$

Câu 5:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = 2 x^{3} - 3 (m + 1) x^{2} + 6 m x$ có hai điểm cực trị $A, B$ sao cho đường thẳng AB vuông góc với đường thẳng : $y = x + 2$ .

A. $[_{m = 2}^{m = - 3}$

B. $[_{m = 3}^{m = - 2}$

C. $[_{m = 2}^{m = 0}$

D. $[_{m = - 3}^{m = 0}$

Xem đáp án

Chọn C

[Phương pháp tự luận]

Ta có : $y = 6 x^{2} - 6 (m + 1) x + 6 m$

Do a + b + c = 6 - 6(m + 1) + 6m = 0 nên

Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1

Hệ số góc đt AB là $k = - {(m - 1)}^{2}$

Đt AB vuông góc với đường thẳng y = x + 2

Câu 6:

Cho hàm số $y = x^{3} - 6 x^{2} + 3 (m + 2) x - m - 6$ . Tìm tất cả các giá trị thực của m để hàm số có 2 cực trị cùng dấu

A. $\frac{- 23}{4} < m < 2$

B. $\frac{- 15}{4} < m < 2$

C. $\frac{- 21}{4} < m < 2$

D. $\frac{- 17}{4} < m < 2$

Xem đáp án

Chọn D

Hàm số có 2 điểm cực trị $x_{1}, x_{2}$ $x_{1}, x_{2}$

$x_{1}, x_{2}$

Chia y cho y’ ta được :

Điểm cực trị tương ứng :

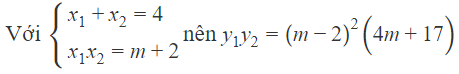
Hai cực trị cùng dấu $\Leftrightarrow y_{1} y_{2} > 0$

$\Leftrightarrow y_{1} y_{2} > 0$

Kết hợp đk : $\frac{- 17}{4}$ $\frac{- 17}{4} < m < 2$

Câu 7:

Cho hàm số $y = 2 x^{3} - 9 x^{2} + 12 x + m$ . Giả sử đồ thị hàm số có hai điểm cực trị là A, B đồng thời A, B cùng với gốc tọa đọ O không thẳng hàng. Khi đó chu vi $∆ O A B$ nhỏ nhất bằng bao nhiêu ?

A. $\sqrt{10} - \sqrt{2}$

B. $\sqrt{10} + \sqrt{2}$

C. $\sqrt{20} - \sqrt{10}$

D. $\sqrt{3} + \sqrt{2}$

Xem đáp án

Chọn B

[Phương pháp tự luận]

Ta có $y^{'} = 6 x^{2} - 18 x + 12$

$y^{'} = 6 x^{2} - 18 x + 12$

$A (1; 5 + m) v à B (2; 4 + m)$ là hai điểm cực trị của đồ thị hàm số

Chu vi của $∆ O A B$ là:

Sử dụng tính chất $|u| + |v| \geq |u + v|$ với $\vec{u} = (1; - 5 - m) v à \vec{v} = (2; 4 + m)$

Từ đó ta có:

Dấu bằng xảy ra khi và chỉ khi $\vec{u}$ , $\vec{v}$ cùng hướng

Vậy chu vi $∆ O A B$ nhỏ nhất bằng $\sqrt{10} + \sqrt{2}$ khi $m = \frac{- 14}{3}$

Câu 8:

Cho hàm số $y = x^{4} - 2 m x^{2} + m - 1$ . Tìm tất cả các giá trị của tham số thưc m để đồ thị hàm số có ba điểm cực trị tạo thành 1 tam giác nhận gốc tọa độ O làm trực tâm

A. m = 4.

B. m = 2.

C. m = 3.

D. m = 1.

Xem đáp án

Chọn D

$y^{'} = 4 x^{3} - 4 m x$

Hàm số có 3 điểm cực trị $\Leftrightarrow m > 0$

Khi đó đồ thị hàm số có 3 điểm cực trị là

A (0 ; m-1)

$B (\sqrt{m}; - m^{2} + m - 1)$

$C (- \sqrt{m}; - m^{2} + m - 1)$

Vì B,C đối xứng nhau qua trục tung nên $B C ⊥ O A$

Do đó O là trực tâm tam giác ABC

Với $\vec{O B} = (\sqrt{m}; - m^{2} + m - 1), \vec{A C} = (- \sqrt{m}; - m^{2})$ $\overset{⇀}{O B} = (\sqrt{m}, - m^{2} + m - 1), \overset{⇀}{A C} = (- \sqrt{m}, - m^{2})$

Từ đó ta có: $- m - m^{2} (- m^{2} + m - 1) = 0$

Vậy m = 1 là gtct

Câu 9:

Tính theo m khoảng cách giữa điểm cực đại và điểm cực tiểu ( nếu có) của đồ thị hàm số: $y = \frac{1}{3} x^{3} - m x^{2} - x + m + 1$

A. $\frac{2}{3} \sqrt{(m^{2} + 1) (4 m^{4} + 5 m^{2} + 9)}$

B. $\frac{4}{9} \sqrt{(2 m^{2} + 1) (4 m^{4} + 8 m^{2} + 13)}$

C. $\frac{2}{3} \sqrt{(m^{2} + 1) (4 m^{4} + 8 m^{2} + 13)}$

D. $\sqrt{(4 m^{2} + 4) (4 m^{4} + 8 m^{2} + 10)}$

Xem đáp án

Chọn C

$e = \frac{m^{2} + 1}{3}$

Câu 10:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = 2 x^{3} + 3 (m - 1) x^{2} + 6 m (1 - 2 m) x$ có điểm cực đại và điểm cực tiểu nằm trên đường thẳng có phương trình: $y = - 4 x (d)$

A. m ∈ {1}

B. m ∈ {0;1}

C. m ∈ {0; $\frac{1}{2}$ ;1}

D. m ∈ { $\frac{1}{2}$ }

Xem đáp án

Chọn A

Câu 11:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = x^{3} + m x^{2} + 7 x + 3$ có đường thẳng đi qua điểm cực đại và điểm cực tiểu vuông góc với đường thẳng có phương trình : $y = 3 x (d)$

A. $m = \pm \sqrt{\frac{45}{2}}$

B. $[_{m = 1}^{m = 0}$

C. m = 2

D. $m = \pm \sqrt{\frac{47}{2}}$

Xem đáp án

Chọn A

[Phương pháp trắc nghiệm]

Bấm máy tính

Đường thẳng đi qua 2 điểm cực trị là

Câu 12:

Tìm các giá trị của tham số m để đồ thị hàm số: y = -x³ + 3x² + 3(m² - 1)x - 3m² - 1 có điểm cực đại và điểm cực tiểu cùng với gốc tọa độ tạo thành tam giác vuông tại O.

A. m = 1

B. $[_{m = \frac{\sqrt{6}}{2}}^{m = - 1}$

C. $[_{m = \pm 1}^{m = \pm \frac{\sqrt{6}}{2}}$

D. m = $\pm$ 1

Xem đáp án

Chọn D

Câu 13:

Tìm các giá trị của tham số m để đồ thị hàm số: y = x³ - 3x² - mx + 2 có điểm cực đại và điểm cực tiểu cách đều đường thẳng có phương trình: $y = x - 1 (d)$

A. m = 0

B. $[_{m = \frac{- 9}{2}}^{m = 0}$

C. m = 2

D. $m = - \frac{9}{2}$

Xem đáp án

Chọn A

[Phương pháp trắc nghiệm]

Hàm số có 2 cực trị m > -3 , gọi x₁, x₂là hai nghiệm của phương trình $y^{'} = 0$

ta có: x₁+ x₂ = 2

Bấm máy tính

Hai điểm cực trị của đồ thị hàm số là

Gọi I là trung điểm của AB

$\Rightarrow I (1; - m)$

Đường thẳng đi qua hai điểm cực trị là

Yêu cầu bài toán

Kết hợp với điều kiện thì m = 0

Câu 14:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = x^{4} - 2 m x^{2} + m - 1$ có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1

A. $[_{m = \pm \frac{- 1 + \sqrt{5}}{2}}^{m = 1}$

B. $[_{m = \frac{- 1 + \sqrt{5}}{2}}^{m = 1}$

C. $m = \pm \frac{- 1 + \sqrt{5}}{2}$

D. m = 1

Xem đáp án

Chọn B

Ta có :

Hàm số đã cho có ba điểm cực trị khi m > 0(*)

Khi đó ba điểm cực trị của đồ thị hàm số là

$A (0; m - 1), B (- \sqrt{m}; - m^{2} + m - 1), C (\sqrt{m}; - m^{2} + m - 1)$

$S_{∆ A B C} = \frac{1}{2} |y_{B} - y_{A}| |x_{c} - x_{B}|$

Kết hợp điều kiện (*) ta có

[Phương pháp trắc nghiệm]

Áp dụng công thức

Kết hợp điều kiện (*) ta có

Câu 15:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = x^{4} - 2 m x^{2} + m - 1$ có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn ngoại tiếp bằng 1

A. $[_{m = \pm \frac{- 1 + \sqrt{5}}{2}}^{m = 1}$

B. $[_{m = \frac{- 1 + \sqrt{5}}{2}}^{m = 1}$

C. $m = \pm \frac{- 1 + \sqrt{5}}{2}$

D. m = 1

Xem đáp án

Chọn B

Ta có :

Hàm số đã cho có ba điểm cực trị khi m > 0(*)

Khi đó ba điểm cực trị của đồ thị hàm số là

$A (0; m - 1), B (- \sqrt{m}; - m^{2} + m - 1), C (\sqrt{m}; - m^{2} + m - 1)$

$S_{∆ A B C} = \frac{1}{2} |y_{B} - y_{A}| |x_{c} - x_{B}|$

Kết hợp điều kiện (*) ta có

[Phương pháp trắc nghiệm]

Áp dụng công thức

Kết hợp điều kiện (*) ta có

Câu 16:

Tìm các giá trị của tham số m để đồ thị hàm số: y = x⁴ - 2m²x² + m⁴ + 1 có ba điểm cực trị . Đồng thời ba điểm cực trị đó cùng với gốc O tạo thành 1 tứ giác nội tiếp

A. m = ±1

B. m = 1

C. Không tồn tại m

D. m = -1

Xem đáp án

Chọn A

$y^{'} = 4 x^{3} - 4 m^{2} x$

Hàm số có 3 điểm cực trị khi m ≠ 0

Khi đó 3 điểm cực trị là

Gọi I là tâm đường tròn ngoại tiếp( nếu có) của tứ giác ABOC .

Do tính chất đối xứng , ta có

A,O,I thẳng hàng

$\Rightarrow A O$ là đường kính của đường tròn ngoại tiếp( nếu có) của tứ giác ABOC

Kết hợp điều kiện $m = \pm 1$ ( thỏa mãn)

Câu 17:

Tìm các giá trị của tham số m để đồ thị hàm số: y = x⁴ - 8m²x² + 1 có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có diện tích bằng 64

A. Không tồn tại m

B. $m = \pm \sqrt[5]{2}$

C. $m = - \sqrt[5]{2}$

D. $m = \sqrt[5]{2}$

Xem đáp án

Chọn D

[Phương pháp trắc nghiệm]

Hàm số có 3 điểm cực trị khi m ≠ 0

Áp dụng công thức

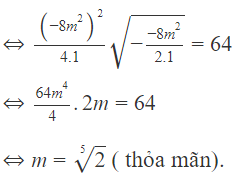
Câu 18:

Tìm các giá trị của tham số m để đồ thị hàm số: y = x⁴ - 2mx² + m có ba điểm cực trị . Đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có bán kính đường tròn nội tiếp lớn hơn 1

A. m < -1

B. m > 2

C. m ∈ (− $\infty$ ,−1) ∪ (2;+ $\infty$ )

D. Không tồn tại m

Xem đáp án

Chọn B

[Phương pháp tự luận]

Hàm số có 3 điểm cực trị khi m > 0

Ba điểm cực trị là

Gọi I là trung điểm của $B C \Rightarrow I (0; m - m^{2})$

$S_{∆ A B C} = \frac{1}{2} A I . B C = m \sqrt{m}$

Chu vi của $∆ A B C$ là:

Bán kính đường tròn nội tiếp $∆ A B C$ là:

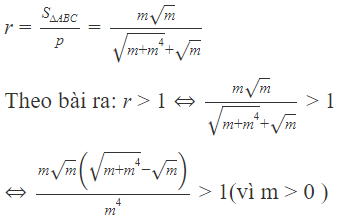
So sánh điều kiện suy ra m > 2 thỏa mãn.

[Phương pháp trắc nghiệm]

Sử dụng công thức

Theo bài ra:

So sánh điều kiện suy ra m > 2 thỏa mãn.

Câu 19:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = x^{4} - (3 m - 1) x^{2} + 2 m + 1$ có ba điểm cực trị. Đồng thời ba điểm cực trị đó cùng với điểm $D (7; 3)$ nội tiếp được một đường tròn

A. m = 3

B. m = 1

C. m = -1

D. Không tồn tại m

Xem đáp án

Chọn A

[Phương pháp trắc nghiệm]

Hàm số có 3 điểm cực trị khi $m > \frac{1}{3}$

Áp dụng công thức:

Phương trình đường tròn ngoại tiếp $∆ A B C$ là:

Thay vào ta có phương trình:

Sử dụng chức năng SOLVE ,

tìm ra nghiệm duy nhất thỏa mãn là m = 3

Câu 20:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = - x^{4} + 2 m x^{2} - 4 m + 1$ có ba điểm cực trị . Đồng thời ba điểm cực trị đó cùng với gốc tọa độ tạo thành 1 hình thoi

A. Không tồn tại m

B. $[_{m = \frac{2 \pm \sqrt{2}}{2}}^{m = \frac{1}{4}}$

C. m = -1

D. m = 1

Xem đáp án

Chọn B

[Phương pháp tự luận]

Hàm số có 3 điểm cực trị khi m > 0

Ba điểm cực trị là:

Tứ giác OBAC đã có OB=OC ,AB=AC.

Vậy tứ giác OBAC là hình thoi chỉ cần thêm điều kiện

( thỏa mãn)

Câu 21:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = - x^{3} + 3 x^{2} + 3 (m^{2} - 1) x - 3 m^{2} - 1$ có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số cách đều gốc tọa độ

A. $m = \pm \frac{1}{2}$

B. $m = \frac{1}{2}$

C. m = −1

D. m = ±1

Xem đáp án

Chọn A

Câu 22:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = x^{3} - 3 m x^{2} + 3 m^{3}$ có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48.

A. m = 2 hoặc m = 0

B. m = 2

C. m = -2

D. m = ±2

Xem đáp án

Chọn D

Đồ thị hàm số có hai điểm cực trị khi và chỉ khi

2m ≠ 0 $\Leftrightarrow m \neq 0$ (1)

Khi đó, các điểm cực trị của đồ thị hàm số là

Ta có: $\vec{O A}$ $\overset{⇀}{O A} (0; 3 m^{3}) \Rightarrow O A = 3 |m^{3}|$

Ta thấy $A \in O y \Rightarrow O A \equiv O y$

$\Rightarrow d (B, O A) = d (B, O y) = 2 |m| (3)$

Từ (2) và (3) suy ra

$S_{∆ O A B} = \frac{1}{2} . O A . d (B, O A) = 3 m^{4}$

Do đó: $S_{∆ O A B} = 48 \Leftrightarrow m = \pm 2$ (thỏa mãn (1)

Câu 23:

Cho hàm số $y = x^{4} - 2 (m + 1) x^{2} + m (C)$ . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số (C) có ba điểm cực trị A, B, C sao cho OA = BC; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung, B và C là hai điểm cực trị còn lại

A. $m = 2 \pm 2 \sqrt{2}$

B. $m = 2 + 2 \sqrt{2}$

C. $m = 2 - 2 \sqrt{2}$

D. m = $\pm 1$

Xem đáp án

Chọn A

Ta có:

Hàm số có 3 điểm cực trị khi và chỉ khi :

$y^{'}$ có 3 nghiệm phân biệt

$\Leftrightarrow m + 1 > 0 \Leftrightarrow m > - 1 (*)$

Khi đó, ta có $y^{'} = 0$

(vai trò của B, C trong bài toán là như nhau ) nên ta giả sử

Do đó OA = BC

$\Leftrightarrow m = 2 \pm 2 \sqrt{2} (t h ỏ a m ã n) (*)$

Vậy $m = 2 \pm 2 \sqrt{2}$

Câu 24:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = x^{3} - 3 m x^{2} + 4 m^{3}$ có các điểm cực đại và cực tiểu đối xứng nhau qua đường thẳng $(d) : y = x$ .

A. $m = \frac{\sqrt{2}}{2}$

B. $m = \frac{- \sqrt{2}}{2}$

C. m=0 hoặc $m = \frac{\sqrt{2}}{2}$

D. $m = \pm \frac{\sqrt{2}}{2}$

Xem đáp án

Chọn D

$y^{'} = 3 x^{2} - 6 m x$

Để hàm số có cực đại và cực tiểu thì m ≠ 0

Giả sử hàm số có hai điểm cực trị là

Trung điểm của đoạn AB là $I (m; 2 m^{3})$

Điều kiện để AB đối xứng nhau qua đường thẳng y = x là AB vuông góc với đường thẳng

$(d) : y = x v à I \in (d)$

Kết hợp với điều kiện ta có $m = \pm \frac{\sqrt{2}}{2}$

Câu 25:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = x^{3} - 3 m x^{2} + 3 (m^{2} - 1) x - m^{3} + m$ có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng $\sqrt{2}$ lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O

A. $m = - 3 - 2 \sqrt{2} h o ặ c m = - 1$

B. $m = - 3 + 2 \sqrt{2} h o ặ c m = - 1$

C. $m = - 3 + 2 \sqrt{2} h o ặ c m = - 3 - 2 \sqrt{2}$

D. $m = - 3 + 2 \sqrt{2}$

Xem đáp án

Chọn C

Ta có $y^{'} = 3 x^{2} - 6 m x + 3 (m^{2} - 1)$

Hàm số (1) có cực trị thì PT $y^{'} = 0$ có 2 nghiệm phân biệt

$\Leftrightarrow x^{2} - 2 m x + m^{2} - 1 = 0$ có 2 nhiệm phân biệt

Khi đó, điểm cực đại $A (m - 1; 2 - 2 m)$ và điểm cực tiểu $B (m + 1; - 2 m)$

Ta có $O A = \sqrt{2} O B \Leftrightarrow m^{2} + 6 m + 1 = 0$

Câu 26:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = x^{4} - 2 m^{2} x^{2} + 1 (C)$ có ba điểm cực trị là ba đỉnh của một tam giác vuông cân

A. m = ±1

B. m = 1 hoặc m = 0

C. m = -1 hoặc m = 0

D. m = -1

Xem đáp án

Chọn A

Ta có:

Hàm số (C) có ba điểm cực trị $\Leftrightarrow m \neq 0$ (*) .

Với điều kiện (*) gọi ba điểm cực trị là:

Do đó nếu ba điểm cực trị tạo thành một tam giác vuông cân, thì sẽ vuông cân tại đỉnh A.

Do tính chất của hàm số trùng phương, tam giác ABC đã là tam giác cân rồi, cho nên để thỏa mãn điều kiện tam giác là vuông, thì AB vuông góc với AC

Tam giác ABC vuông khi:

Vậy với $m = \pm 1$ thì thỏa mãn yêu cầu bài toán.

[Phương pháp trắc nghiệm]

Yêu cầu bài toán

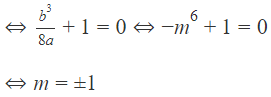
Câu 27:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = m x^{3} - 3 m x^{2} + 3 m - 3$ có hai điểm cực trị A,B sao cho $2 A B^{2} - (O A^{2} + O B^{2}) = 20$ ( Trong đó O là gốc tọa độ).

A. m = -1

B. m = 1

C. m = −1 hoặc m = − $\frac{17}{11}$

D. m = 1 hoặc m = − $\frac{17}{11}$

Xem đáp án

Chọn D

Ta có: $y^{'} = m (3 x^{2} - 6 x)$

Với mọi m ≠ 0, ta có $y^{'} = 0$

Vậy hàm số luôn có hai điểm cực trị.

Giả sử $A (0; 3 m - 3); B (2; - m - 3)$

Ta có

Vậy giá trị m cần tìm là:

Câu 28:

Cho hàm số $y = x^{3} - 3 x^{2} (C)$ .Tìm tất cả các giá trị thực tham số m để đường thẳng đi qua 2 điểm cực trị của đồ thị (C) tạo với đường thẳng $∆ : x + m y + 3 = 0$ một góc $α$ biết $\cos α = \frac{4}{5}$

A. $m = 2 h o ặ c m = - \frac{2}{11}$

B. $m = - 2 h o ặ c m = - \frac{2}{11}$

C. $m = 2 h o ặ c m = \frac{2}{11}$

D. m = 2

Xem đáp án

Chọn A

Đường thẳng đi qua ĐCĐ, ĐCT là $∆_{1} : 2 x + y = 0 c ó V T P T n_{1} (2; 1)$ $∆_{1} : 2 x + y = 0 c ó V T P T n_{1} (2; 1)$

Đường thẳng đã cho có $∆ : x + m y + 3 = 0 c ó V T P T n_{2} (1; m)$

Yêu cầu bài toán

Câu 29:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = x^{4} - 4 (m - 1) x^{2} + 2 m - 1$ có 3 điểm cực trị tạo thành 3 đỉnh của một tam giác đều

A. m = 0

B. m = 1

C. $m = 1 + \frac{\sqrt[3]{3}}{2}$

D. $m = 1 - \frac{\sqrt[3]{3}}{2}$

Xem đáp án

Chọn C

Ta có

nên hàm số có 3 điểm cực trị khi m > 1.

Với đk m > 1 đồ thị hàm số có 3 điểm cực trị là:

Ta có:

Để 3 điểm cực trị của đồ thị hàm số tạo thành tam giác đều thì:

So sánh với điều kiện ta có: $m = 1 + \frac{\sqrt[3]{3}}{2}$ thỏa mãn.

[Phương pháp trắc nghiệm]

Yêu cầu bài toán

Câu 30:

Tìm tất cả các giá trị thực của tham số m để điểm M ( 2m³; m) tạo với hai điểm cực đại, cực tiểu của đồ thị hàm số y = 2x³ - 3(2m + 1)x² + 6m(m + 1)x + 1 một tam giác có diện tích nhỏ nhất