30 câu hỏi trắc nghiệm thuộc Bài tập số phức mức độ cơ bản, nâng cao cực hay có lời giải chi tiết(P1)

Câu 1:

Cho số phức $z = {(1 - 2 i)}^{2}$ , số phức liên hợp của z là

A. $\bar{z}$ = 3 - 4i

B. $\bar{z}$ = -3 + 4i

C. $\bar{z}$ = -3 - 4i

D. $\bar{z}$ = 1 + 2i

Xem đáp án

Đáp án B

$z = {(1 - 2 i)}^{2} = 1 - 4 i + 4 i^{2} = 1 - 4 i - 4 = - 3 - 4 i \Rightarrow \bar{z} = - 3 + 4 i$

Câu 2:

Cho hai số phức $z_{1} = - 1 + 2 i, z_{2} = - 1 - 2 i$ . Giá trị của biểu thức ${|z_{1}|}^{2} + {|z_{2}|}^{2}$ bằng

A. $\sqrt{10}$

B. 10

C. -6

D. 4

Xem đáp án

Đáp án B

$z_{1} = - 1 + 2 i \Rightarrow |z_{1}| = \sqrt{{(- 1)}^{2} + 2^{2}} = \sqrt{5} z_{2} = - 1 - 2 i \Rightarrow |z_{2}| = \sqrt{{(- 1)}^{2} + {(- 2)}^{2}} = \sqrt{5} \Rightarrow {|z_{1}|}^{2} + {|z_{2}|}^{2} = 5 + 5 = 10$

Câu 3:

Biết phương trình $z^{2} + a z + b = 0 (a, b \in ℝ)$ có một nghiệm là z = -2 + i. Tính a + b

A. 9.

B. 1.

C. 4

D. -1

Xem đáp án

Đáp án A

$Ta dễ dàng suy ra nghiệm còn lại của phương trình là z_{2} = - 2 - i Áp dụng hệ thức Vi - ét : \{\begin{cases} z_{1} + z_{2} = - 2 + i - 2 - i = - a \Rightarrow a = 4 \\ z_{1} z_{2} = (- 2 + i) (- 2 - i) = {(- 2)}^{2} - i^{2} = 4 + 1 = 5 = b \end{cases} \Rightarrow a + b = 4 + 5 = 9$

Câu 4:

Cho số phức z thỏa mãn phương trình 4|z+i| + 3|z-i| = 10. Tính giá trị nhỏ nhất của |z|

A. $\frac{1}{2}$

B. $\frac{5}{7}$

C. $\frac{3}{2}$

D. 1

Xem đáp án

Đáp án D

$Đặt z = a + bi (a; b \in ℝ) Ta có : |z + i| = \sqrt{a^{2} + {(b + 1)}^{2}} = \sqrt{a^{2} + b^{2} + 2 b + 1} = \sqrt{{|z|}^{2} + 2 b + 1} Tương tự : |z - i| = \sqrt{{|z|}^{2} - 2 b + 1} Áp dụng BĐT bunhiacopski dạng (a^{2} + b^{2}) (c^{2} + d^{2}) \leq {(ac + bd)}^{2} \Rightarrow 4 |z + i| + 3 |z - i| \leq \sqrt{4^{2} + 3^{2}} . \sqrt{{|z + i|}^{2} + {|z - i|}^{2}} \Leftrightarrow 10 \leq 5 \sqrt{{|z|}^{2} + 2 b + 1 + {|z|}^{2} - 2 b + 1} = 5 \sqrt{2 {|z|}^{2} + 2} \Leftrightarrow 4 \leq 2 {|z|}^{2} + 2 \Leftrightarrow {|z|}^{2} \geq 1 \Leftrightarrow |z| \geq 1 KL : {|z|}_{\min} = 1$

Câu 5:

Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức z = (1+i)(2-i)?

A. P

B. M

C. N

D. Q

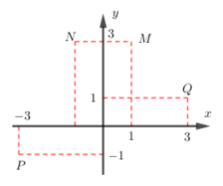
Xem đáp án

Đáp án D

$z = (1 + i) (2 - i) = 2 - i + 2 i - i^{2} = 2 + i + 1 = 3 + i \Rightarrow Điểm biểu diễn số phức z là Q (3; 1)$

Câu 6:

Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn | $\bar{z}$ +2-i| = 4 là đường tròn có tâm I và bán kính R lần lượt là

A. I(-2;-1), R = 4

B. I(-2;-1), R = 2

C. I(2;-1), R = 4

D. I(2;-1), R = 2

Xem đáp án

Đáp án A

$Gọi z = a + bi (a; b \in ℝ) \Rightarrow \bar{z} = a - bi \Rightarrow |\bar{z} + 2 - i| = |a + 2 - (b + 1) i| = \sqrt{{(a + 2)}^{2} + {(b + 1)}^{2}} = 4 \Rightarrow {(a + 2)}^{2} + {(b + 1)}^{2} = 16 KL : Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn đề bài nằm trên đường tròn tâm I (- 2; - 1), bán kính R = 4$

Câu 7:

Cho số phức z = x + yi (a,b $\in ℝ$ ) thỏa mãn $|\frac{z - 1}{z - i}| = 1 và |\frac{z - 3 i}{z + i}| = 1$ . Tính P = x + y.

A. P = 7

B. P = -1

C. P = 1

D. P = 2

Xem đáp án

Đáp án D

Câu 8:

Điểm M trong hình vẽ là biểu diễn hình học của số phức nào dưới đây?

A. z = 2 - i

B. z = 2 + i

C. z = -1 + 2i

D. z = -1 - 2i

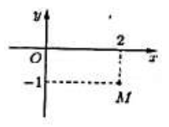
Xem đáp án

Đáp án A

Điểm M(2;-1) biểu diễn số phức z = 2-i

Câu 9:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z-1+i| = 2 là đường tròn có tâm và bán kính lần lượt là

A. I(-1;1), R = 4

B. I(-1;1), R = 2

C. I(1;-1), R = 2

D. I(1;-1), R = 4

Xem đáp án

Đáp án C

Gọi z = x+yi (x;y $\in ℝ$ )

$\Rightarrow |z - 1 + i| = |x - 1 + (y + 1) i| = \sqrt{{(x - 1)}^{2} + {(y + 1)}^{2}} = 2 \Rightarrow {(x - 1)}^{2} + {(y + 1)}^{2} = 4 KL : Tập hợp các điểm biểu diễn số phức z thỏa mãn yêu cầu bài toán năm trên đường tròn tâm I (1; - 1) có bán kính R = 2 Tổng quát : Nếu số phức z thỏa mãn |z - a + bi| = c thì tập hợp các điểm thỏa mãn nằm trên đường tròn tâm I (a; - b) có bán kính R = c$

Câu 10:

Gọi $z_{1} v à z_{2}$ là hai nghiệm phức của phương trình $z^{2}$ + 2z + 10 = 0. Giá trị của $|z_{1}^{2}| + |z_{2}^{2}|$ bằng

A. $\sqrt{10}$

B. 20

C. 2 $\sqrt{10}$

D. 10

Xem đáp án

Đáp án B

$Giải PT : z^{2} + 2 z + 10 = 0 \Leftrightarrow \{\begin{cases} z_{1} = - 1 + 3 i \\ z_{2} = - 1 - 3 i \end{cases} \Rightarrow |z_{1}^{2}| = |{(- 1 + 3 i)}^{2}| = |1 - 6 i + 9 i^{2}| = |- 8 - 6 i| = 10 tương tự : |z_{2}^{2}| = |{(- 1 - 3 i)}^{2}| = |1 + 6 i + 9 i^{2}| = |- 8 + 6 i| = 10 \Rightarrow |z_{1}^{2}| + |z_{2}^{2}| = 10 + 10 = 20$

Câu 11:

Cho hai số thực x,y thỏa mãn x(3+2i) + y(1-4i) = 11+12i. Giá trị của x + y bằng

A. 3.

B. -7.

C. –3.

D. 7.

Xem đáp án

Đáp án A

$Ta có : x (3 + 2 i) + y (1 - 4 i) = 3 x + y + (2 x - 4 y) i = 11 + 12 i \Rightarrow \{\begin{array}{l} 3 x + y = 11 \\ 2 x - 4 y = 12 \end{array} \Leftrightarrow \{\begin{cases} x = 4 \\ y = - 1 \end{cases} \Rightarrow x + y = 4 - 1 = 3$

Câu 12:

Tìm hai số thực x và y thỏa mãn (2x-3yi) + (1-3i) = x + 6i với i là đơn vị ảo.

A. x = -1; y = -3

B. x = -1; y = -1

C. x = 1; y = -1

D. x = 1; y = -3

Xem đáp án

Đáp án A

$(2 x - 3 yi) + 1 - 3 i = 2 x + 1 - (3 y + 3) i = x + 6 i \Rightarrow \{\begin{array}{l} 2 x + 1 = x \\ 3 y + 3 = - 6 \end{array} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = - 3 \end{cases}$

Câu 13:

Xét các số phức z thỏa mãn ( $\bar{z}$ +i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng

A. 1

B. $\frac{5}{4}$

C. $\frac{\sqrt{5}}{2}$

D. $\frac{\sqrt{3}}{2}$

Xem đáp án

Đáp án C

$Gọi z = a + bi (a; b \in ℝ) \Rightarrow \bar{z} = a - bi \Rightarrow (\bar{z} + i) (z + 2) = (a - bi + i) (a + bi + 2) = [a + (1 - b) i] [a + 2 + bi] = a (a + 2) + abi + (a + 2) (1 - b) i + b (1 - b) i^{2} = a^{2} + 2 a - b (1 - b) + [ab + (a + 2) (1 - b)] i = a^{2} + 2 a + b^{2} - b + (a + 2 - 2 b) i (*) Để (*) là số thuần ảo thì a^{2} + 2 a + b^{2} - b = 0 \Leftrightarrow {(a + 1)}^{2} + {(b - \frac{1}{2})}^{2} - \frac{1}{4} - 1 = 0 \Leftrightarrow {(a + 1)}^{2} + {(b - \frac{1}{2})}^{2} = \frac{5}{4} \Rightarrow Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I (- 1; \frac{1}{2}), bán kính R = \frac{\sqrt{5}}{2}$

Câu 14:

Có bao nhiêu số phức z thỏa mãn |z|(z-4-i) + 2i = (5-i)z?

A. 2

B. 3

C. 1

D. 4

Xem đáp án

Đáp án B

Câu 15:

Số phức -3 + 7i có phần ảo bằng

A. 3.

B. -7.

C. –3.

D. 7.

Xem đáp án

Đáp án D

Số phức z = a+bi có phần thực là a, phần ảo là b nên

Số phức z = -3+7i có phần ảo là 7

Câu 16:

Phần ảo của số phức z = 5 + 2i bằng:

A. 5

B. 5i

C. 2

D. 2i

Xem đáp án

Đáp án C

Số phức z = a+bi có phần thực là a, phần ảo là b nên

Số phức z = 5+2i có phần ảo là 2

Câu 17:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z+2| = |z-i| là một đường thẳng có phương trình

A. 4x + 2y + 3 = 0

B. 2x + 4y + 13 = 0

C. 2x - 4y + 13 = 0

D. $\{\begin{cases} x = 4 + t \\ y = - 2 + t \\ z = 1 + t \end{cases}$

Xem đáp án

Đáp án A

$Đặt z = a + bi (a; b \in ℝ) |z + 2| = |z - i| \Leftrightarrow |a + 2 + bi| = |a + (b - 1) i| \Leftrightarrow {(a + 2)}^{2} + b^{2} = a^{2} + {(b - 1)}^{2} \Leftrightarrow 4 a + 4 = - 2 b + 1 \Leftrightarrow 4 a + 2 b + 3 = 0 KL : Tập hợp các điểm biểu diễn số phức z thoả mãn yêu cầu đề bài nằm trên đường thẳng 4 x + 2 y + 3 = 0$

Câu 18:

Cho z là số phức thỏa mãn | $\bar{z}$ | = |z+2i|. Giá trị nhỏ nhất của |z-1+2i| + |z+1+3i| là

$A . \sqrt{5}$

$B . 5 \sqrt{2}$

$C . \sqrt{13}$

$D . \sqrt{29}$

Xem đáp án

Đáp án C

Câu 19:

Cho số phức z = 6 + 7i. Số phức liên hợp của z là

A. $\bar{z}$ = 6 + 7i

B. $\bar{z}$ = -6 + 7i

C. $\bar{z}$ = -6 - 7i

D. $\bar{z}$ = 6 - 7i

Xem đáp án

Đáp án D

Số phức z = 6+7i có số phức liên hợp là $\bar{z} = 6 - 7 i$

Câu 20:

Tính mô đun của số phức z, biết (1-2i)z + 2 - i = -12i

A. 5

B. $\sqrt{7}$

C. $\frac{1}{5}$

D. $2 \sqrt{2}$

Xem đáp án

Đáp án A

$(1 - 2 i) z + 2 - i = - 12 i \Leftrightarrow (1 - 2 i) z = - 2 - 11 i \Leftrightarrow z = \frac{- 2 - 11 i}{1 - 2 i} = \frac{(- 2 - 11 i) (1 + 2 i)}{1^{2} - 4 i^{2}} = \frac{20 - 15 i}{5} = 4 - 3 i \Rightarrow |z| = \sqrt{4^{2} + {(- 3)}^{2}} = 5$

Câu 21:

Cho số phức z thỏa mãn $3 |z + \bar{z}| + 2 |z - \bar{z}| \leq 12$ . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của |z-4+3i|. Giá trị M.m bằng

A. 20

B. 24

C. 26

D. 28

Xem đáp án

Đáp án B

Câu 22:

Tập hợp các điểm M biểu diễn số phức z sao cho $z^{2} = {(\bar{z})}^{2}$ là

A. Trục tung và trục hoành.

B. Trục tung.

C. Trục hoành.

D. Gốc tọa độ.

Xem đáp án

Đáp án A

$Đặt z = x + yi (x; y \in ℝ) \Rightarrow \bar{z} = x - yi Theo đề bài : z^{2} = {(\bar{z})}^{2} \Leftrightarrow {(x + yi)}^{2} = {(x - yi)}^{2} \Leftrightarrow x^{2} + 2 xyi - y^{2} = x^{2} - 2 xyi - y^{2} \Leftrightarrow 4 xyi = 0 \Leftrightarrow x = 0 hoặc y = 0 KL : Tập hợp các điểm M biểu diễn số phức z thỏa mãn yêu cầu bài toán nằm trên trục hoành hoặc nằm trên trục tung$

Câu 23:

Gọi $z_{1}; z_{2}$ là hai nghiệm phức của phương trình $z^{2} - 4 z + 5 = 0$ . Khi đó phần thực của $z_{1}^{2} + z_{2}^{2}$ là

A. 7.

B. 5.

C. 4.

D. 6.

Xem đáp án

Đáp án D

Giải PT:

$z^{2} - 4 z + 5 = 0 \Leftrightarrow \{\begin{cases} z_{1} = 2 + i \\ z_{2} = 2 - i \end{cases} \Rightarrow z_{1}^{2} + z_{2}^{2} = {(2 + i)}^{2} + {(2 - i)}^{2} = 6$

Câu 24:

Cho hai số phức z, w thỏa mãn $\{\begin{cases} | z - 3 - 2 i | \leq 1 \\ | w + 1 + 2 i | \leq | w - 2 - i | \end{cases}$ . Tìm gía trị nhỏ nhất $P_{m i n}$ của biểu thức P = |z-w|.

$A . P_{m i n} = \frac{3 \sqrt{2} - 2}{2}$

$B . P_{m i n} = \sqrt{2} + 1$

$C . P_{m i n} = \frac{5 \sqrt{2} - 2}{2}$

$D . P_{m i n} = \frac{2 \sqrt{2} + 1}{2}$

Xem đáp án

Đáp án C

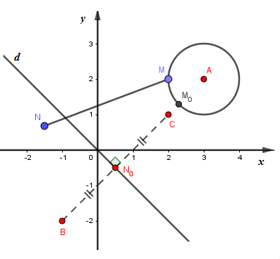
Đặt $A (3; 2), B (- 1; - 2), C (2; 1)$ . Gọi M, N lần lượt là điểm biểu diến của z, w.

Vì $| z - 3 - 2 i | \leq 1$ nên tập hợp điểm biểu diễn của z trên hệ trục Oxy là hình tròn tâm A bán kính 1.

Vì $| w + 1 + 2 i | \leq | w - 2 - i |$ nên tập hợp điểm biểu diễn của w trên hệ trục Oxy là nửa mặt phẳng bờ d chứa B và đường thẳng d. Trong đó d là trung trực của đoạn thẳng BC.

$P = | z - w | = M N$ , $P_{\min} = {MN}_{\min}$

Dễ dàng kiểm tra được A, B, C thẳng hàng và MN ngắn nhất khi MN trùng với $M_{0} N_{0}$

Trong đó, $N_{0}$ : trung điểm của BC, $M_{0}$ : giao của AB và đường tròn $(A; 1)$

Độ dài đoạn $M_{0} N_{0} = d (A; d) - R = d (A; d) - 1$

Phương trình đường thẳng d có:

$N_{0}$ là trung điểm BC $\Rightarrow N_{0} (\frac{1}{2}; \frac{- 1}{2})$

$\vec{B C} = (3; 3) \Rightarrow d$ $d có 1 VTPT là (1; 1)$

Phương trình đường thẳng d: $1 (x - \frac{1}{2}) + 1 (y - \frac{- 1}{2}) = 0 \Leftrightarrow x + y = 0$

$d (A; d) = \frac{| 3 + 2 |}{\sqrt{1^{2} + 1^{2}}} = \frac{5}{\sqrt{2}} \Rightarrow M_{o} N_{0} = \frac{5}{\sqrt{2}} - 1 = \frac{5 \sqrt{2} - 2}{2}$

Vậy, $P_{min} = \frac{5 \sqrt{2} - 2}{2}$

Câu 25:

Cho các góc $α, β$ và có số phức z = cos $α$ + i.sin $β$ . Khi đó x = z.w thì:

$A . x = \cos (α - β) + i . \sin (α + β)$

$B . x = \cos (α + β) + i . \sin (α + β)$

$C . x = \cos (α β) + i . \sin (α β)$

$D . x = \sin (α - β) + i . \cos (α + β)$

Xem đáp án

Đáp án B

Câu 26:

Biết các số phức z,w khác 0 thỏa mãn: $z^{2} + w^{2}$ = zw Khi đó:

$A . z^{6} = w^{6}$

$B . z^{5} = w^{5}$

$C . z^{4} = i w^{4}$

$D . z^{3} + i w^{3} = 0$

Xem đáp án

Đáp án A

Câu 27:

Biết số phức z thỏa mãn: $\frac{z + 1}{z - 1}$ là số thuần ảo. Khi đó ta phải có:

$A . i z \notin ℝ$

$B . | z | = 4$

$C . | z | = 1$

$D . z = \frac{1}{2} - i . \frac{\sqrt{3}}{2}$

Xem đáp án

Đáp án C

$Đặt z = a + bi (a; b \in ℝ) \Rightarrow \frac{z + 1}{z - 1} = 1 + \frac{2}{z - 1} = 1 + \frac{2}{a - 1 + bi} = 1 + \frac{2 (a - 1 - bi)}{{(a - 1)}^{2} + b^{2}} = 1 + \frac{2 (a - 1)}{{(a - 1)}^{2} + b^{2}} - \frac{2 b}{{(a - 1)}^{2} + b^{2}} i Để \frac{z + 1}{z - 1} là số thuần ảo thì \{\begin{cases} 1 + \frac{2 (a - 1)}{{(a - 1)}^{2} + b^{2}} = 0 \\ \frac{- 2 b}{{(a - 1)}^{2} + b^{2}} \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} b \neq 0 \\ {(a - 1)}^{2} + b^{2} + 2 (a - 1) = 0 \end{cases} \Leftrightarrow \{\begin{cases} b \neq 0 \\ a^{2} + b^{2} = 1 \end{cases} \Rightarrow |z| = 1$

Câu 28:

Biết $1 + i + i^{2} + . . . . + i^{100} = a + b i (a, b \in ℝ)$ . Tìm a,b.

$A . \{\begin{cases} a = 0 \\ b = 1 \end{cases}$

$B . \{\begin{cases} a = 1 \\ b = 0 \end{cases}$

$C . \{\begin{cases} a = 1 \\ b = 1 \end{cases}$

$D . \{\begin{cases} a = - 1 \\ b = - 1 \end{cases}$

Xem đáp án

Đáp án B

$Ta có i^{2 k} + i^{2 k + 2} = i^{2 k} (1 + i^{2}) = 0 và i^{2 k + 1} + i^{2 k + 3} = i^{2 k + 1} (1 + i^{2}) = 0 \Rightarrow 1 + i + i^{2} + . . . + i^{100} = 1 + (i + i^{3}) + (i^{2} + i^{4}) + . . . + (i^{97} + i^{99}) + (i^{98} + i^{100}) = 1 + 0 + 0 + . . . + 0 + 0 = 1 = a + bi \Rightarrow \{\begin{cases} a = 1 \\ b = 0 \end{cases}$

Câu 29:

Tìm phần thực a của số phức $z = \frac{1 - i . \tan \frac{π}{7}}{1 + i . \tan \frac{π}{7}}$

A. a = 1

B. a = $\sin \frac{2 π}{7}$

C. a = $\tan \frac{π}{7}$

D. a = $\cos \frac{2 π}{7}$

Xem đáp án

Đáp án D

$z = \frac{1 - i . \tan \frac{π}{7}}{1 + i . \tan \frac{π}{7}} = \frac{(1 - i . \tan \frac{π}{7}) (1 - i . \tan \frac{π}{7})}{1 - i^{2} . \tan^{2} \frac{π}{7}} = \frac{1 - \tan^{2} \frac{π}{7} - 2 i . \tan \frac{π}{7}}{1 + \tan^{2} \frac{π}{7}} \Rightarrow Phần thực của số phức z là : a = \frac{1 - \tan^{2} \frac{π}{7}}{1 + \tan^{2} \frac{π}{7}} = \frac{\cos^{2} \frac{π}{7} - \sin^{2} \frac{π}{7}}{\cos^{2} \frac{π}{7} + \sin^{2} \frac{π}{7}} = \cos \frac{2 π}{7}$

Câu 30:

Biết z thỏa mãn |z - 2i + 1| thì |z + i| đạt giá trị nhỏ nhất là bao nhiêu? (z' = z + i)

$A . | z |_{m i n} = 3 - \sqrt{5}$

$B . | z |_{m i n} = \frac{1}{3}$

$C . | z |_{m i n} = \sqrt{10} - 3$

$D . | z |_{m i n} = 3 + \sqrt{5}$

Xem đáp án

Đáp án C

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập số phức mức độ cơ bản, nâng cao cực hay có lời giải chi tiết

Bài tập số phức mức độ cơ bản, nâng cao cực hay có lời giải chi tiết(P1)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm