Đề kiểm tra Học kì 1 Toán 12 có đáp án (Mới nhất) (Đề 10)
-
3052 lượt thi
-
42 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hàm số có đồ thị là hình nào sau đây?
 Xem đáp án
Xem đáp án
Chọn B
Hàm số đã cho là hàm trùng phương, có hệ số a > 0 nên loại câu C và D.
Hàm số có hệ số a = 1 và b = 2 cùng dấu nên hàm số chỉ có một cực trị. Loại A.
Câu 2:
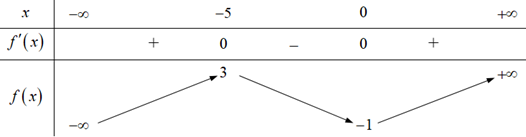
 Xem đáp án
Xem đáp án
Chọn D
Ta thấy nên hàm số nghịch biến trên .Câu 3:
 Xem đáp án
Xem đáp án
Chọn B
Ta có là tiệm cận ngang của đồ thị hàm số.Câu 5:
 Xem đáp án
Xem đáp án
Chọn B
Ta có ; và y' đổi dấu khi qua điểm x = 0 nên hàm số có 1 điểm cực trị.
Chú ý: Hàm số dạng trùng phương có các hệ số a = -1, b = -2017 cùng dấu nên hàm số có 1 điểm cực trị.Câu 6:
 Xem đáp án
Xem đáp án
Chọn A
Đáp án A đúng vì ta có nên .
Đáp án B sai vì .
Đáp án C sai vì .
Đáp án D sai vì .Câu 7:
 Xem đáp án
Xem đáp án
Chọn C
Lý thuyết: Đồ thị các hàm số và đối xứng nhau qua đường thẳng .
Đáp án A sai vì đồ thị các hàm số và đối xứng nhau qua trục tung.
Đáp án B sai vì đồ thị hàm số và đối xứng nhau qua trục hoành.
Câu 8:
Cho các khẳng định sau:
(I). Hình chóp đều là hình chóp có đáy là đa giác đều và đường cao hạ từ đỉnh qua tâm của đáy.
(II). Hình hộp là lăng trụ có đáy là hình chữ nhật.
(III). Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều.
(IV). Hình lập phương có 9 mặt phẳng đối xứng.
Số khẳng định đúng là? Xem đáp án
Xem đáp án
Chọn C
Các khẳng định đúng là (I), (III), (IV).
Câu 9:
Cho các khẳng định sau:
(I). Tứ diện đều có 6 mặt phẳng đối xứng.
(II). Hình hộp chữ nhật 3 kích thước khác nhau có 3 mặt phẳng đối xứng.
(III). Lăng trụ tam giác đều có 4 mặt phẳng đối xứng.
(IV). Bát diện đều có 9 mặt phẳng đối xứng.
Số khẳng định Sai là? Xem đáp án
Xem đáp án
Chọn A
Câu 10:
Thể tích khối nón tròn xoay có đường cao h, đường sinh l, bán kính đáy R có thể tích là.
 Xem đáp án
Xem đáp án
Câu 11:
 Xem đáp án
Xem đáp án
Chọn D
Phương trình hoành độ giao điểm của hai đồ thị là
.
Suy ra hai đồ thị có ba điểm chung.Câu 15:
 Xem đáp án
Xem đáp án
Chọn D
Tập xác định: D = R.
.
Hàm số luôn đồng biến trên R.Câu 16:
 Xem đáp án
Xem đáp án
Chọn A
Để đồ thị hàm số có đúng một tiệm cận đứng thì phương trình có duy nhất nghiệm khác 1 hoặc có hai nghiệm phân biệt trong đó có một nghiêm bằng 1.
TH1:
Khi m = 3, phương trình có một nghiệm x = 3 (thỏa mãn).
Khi m = -3 phương trình có một nghiệm x = -3 (thỏa mãn).
TH2: Phương trình (*) có một nghiệm bằng 1
Thử lại, với m = 5 ta có phương trình (thỏa mãn)
Vậy với m = 3, m = -3, m = 5 thì đồ thị hàm số có duy nhất một tiệm cận đứng.Câu 17:
 Xem đáp án
Xem đáp án
Chọn C
hàm số nghịch biến trên [-2;0]
.
Câu 18:
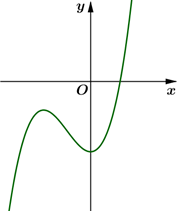
 Xem đáp án
Xem đáp án
Chọn B
Dựa vào đồ thị, ta có các nhận xét sau:
+ Ta thấy rằng .
+ Hàm số đạt cực đại tại . Ta có là nghiệm phương trình
Theo hệ thức Viét, ta có
+ Đồ thị hàm số đi qua điểm có tọa độ .
Vậy các hệ số .Câu 19:
 Xem đáp án
Xem đáp án
Chọn D
Điều kiện: .
Bất phương trình .
So với điều kiện, ta cóCâu 20:
 Xem đáp án
Xem đáp án
Chọn C
Ta có .
Vậy .
Câu 21:
 Xem đáp án
Xem đáp án
Chọn D
Hàm số có tập xác định là R .
Câu 22:
 Xem đáp án
Xem đáp án
Chọn C
Ta có .
Đặt . Ta có ; .
Bảng biến thiên: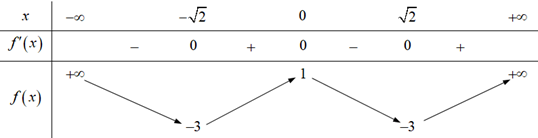
Câu 23:
 Xem đáp án
Xem đáp án
Chọn C
+ Các khẳng định A, B sai theo lý thuyết.
+ Xét khẳng định C: Ta có hàm số đồng biến trên R => C đúng.
+ Xét khẳng định D: Ta có hàm số đồng biến trên => D sai.Câu 24:
 Xem đáp án
Xem đáp án
Chọn C
Ta có
.
Vì nên . Vậy có tất cả 6 nghiệm nguyên.
Câu 25:
Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a. Thể tích của (H) bằng.
 Xem đáp án
Xem đáp án
Chọn B
Giả sử tứ diện đều S.ABCD.
Tính diện tích ABCD: .
Xác định chiều cao:
Gọi là chiều cao của khối chóp.
vuông tại O cho ta .
Vậy, .Câu 26:
 Xem đáp án
Xem đáp án
Chọn D
.
Câu 27:
 Xem đáp án
Xem đáp án
Chọn B
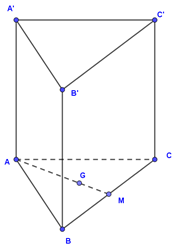
Giả sử khối lăng trụ tam giác đều là ABC.A'B'C' ; gọi G là trọng tâm tam giác ABC.
Gọi h là chiều cao của khối lăng trụ và x là độ dài cạnh tam giác đáy.
Do đáy là tam giác đều cạnh x nên có diện tích : .
Thể tích của khối lăng trụ tam giác đều là: .
Bán kính đường tròn đáy của khối trụ ngoại tiếp là .
Thể tích khối trụ là :.
Câu 28:
 Xem đáp án
Xem đáp án
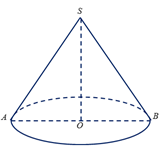
Gọi l, h, R lần lượt là độ dài đường sinh, đường cao và bán kính đáy của hình nón.
Thiết diện qua trục của hình nón là tam giác SAB vuông cân tại S có cạnh huyền .
Nên .
Ta có: .
Vậy diện tích xung quanh của hình nón: .
Câu 29:
 Xem đáp án
Xem đáp án
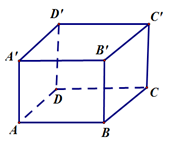
Đặt cạnh lập phương là a.
Tổng diện tích các mặt lập phương là: .
Theo bài ta có: .
Vậy thể tích khối lập phương là : .
Câu 30:
 Xem đáp án
Xem đáp án
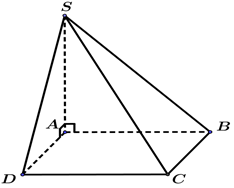
Diện tích hình chữ nhật ABCD là: .
là đường cao của chóp S.ABCD.
Thể tích khối chóp S.ABCD là:Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
Chọn A
Ta có .
Hàm số có hai điểm cực trị .
Khi đó hai điểm cực trị là ,
.
Vectơ chỉ phương của đường thẳng là .
Đường thẳng AB vuông góc với đường thẳng
Vậy m = 0 hoặc m = 2
Câu 32:
 Xem đáp án
Xem đáp án
Chọn C
Điều kiện: .
Khi đó,
* TH1: : Ta có
.
* TH2: :
.
Vậy .
Câu 33:
 Xem đáp án
Xem đáp án
Chọn A
Ta có .
Hàm số nghịch biến trên khoảng khi y' < 0, .
Đồng thời .
Ta có
Vậy .
Câu 34:
 Xem đáp án
Xem đáp án
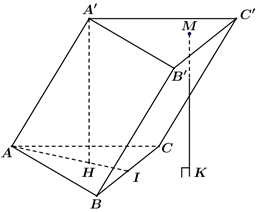
Gọi h là chiều cao của lăng trụ, . Khi đó chóp M.ABC có chiều cao là h.
Thể tích lăng trụ V = hS.
Thể tích tứ diện M.ABC là .
Câu 35:
 Xem đáp án
Xem đáp án
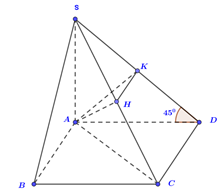
Ta có: (SAB) và (SAD) cùng vuông góc với mặt phẳng đáy
Câu 37:
 Xem đáp án
Xem đáp án
Chọn A
Đặt , . Ta có .
Khi đó phương trình trở thành
Xét hàm số trên khoảng , có .
Suy ra f(t) là hàm số nghịch biến trên , kết hợp với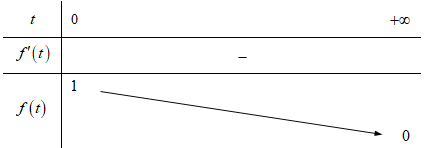
Vậy phương trình (*) có nghiệm khi và chỉ khi 0 < m < 1.
Câu 38:
 Xem đáp án
Xem đáp án
Chọn C
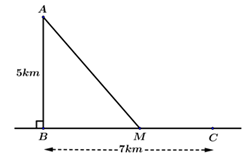
Đặt . Khi đó , .
Thời gian người canh hải đăng đi từ A đến C là (giờ)
Ta có: (km)
Hàm số F(x) đạt giá trị nhỏ nhất tại điểm do đó (km).
Câu 39:
 Xem đáp án
Xem đáp án
Chọn C
Gọi N là số tiền gốc gửi vào sổ tiết kiệm, lãi suất là r, A là số tiền hàng tháng mà anh ta rút ra. Ta có:
Sau tháng thứ 1 số tiền trong sổ còn lại là: ![]() .
.
Sau tháng thứ 2 số tiền trong sổ còn lại là: 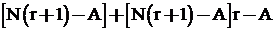
![]() .
.
Sau tháng thứ 3 số tiền trong sổ còn lại là: ![]()
![]() .
.
…………………………………………………………………
Sau tháng thứ n số tiền trong sổ còn lại là:
![]()
![]() .
.
Nếu sau tháng thứ n số tiền trong sổ anh ta vừa hết thì 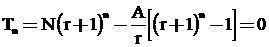
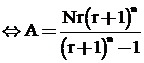 .
.
Câu 40:
 Xem đáp án
Xem đáp án
Chọn C
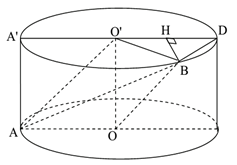
Kẻ đường sinh AA'. Gọi D là điểm đối xứng với A qua O' và H là hình chiếu của B trên đường thẳng A'D.
Do 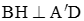 ,
, 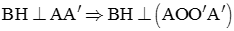 .
.
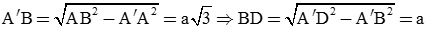
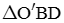 đều nên
đều nên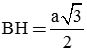 .
.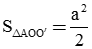 . Suy ra thể tích khối tứ diện
. Suy ra thể tích khối tứ diện 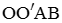 là:
là: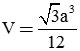 .
.Câu 41:
 Xem đáp án
Xem đáp án
Ta có ![]() .
.
Hàm số có hai điểm cực trị x1, x2 <=> phương trình ![]() có hai nghiệm phân biệt
có hai nghiệm phân biệt ![]() .
.
Ta có ![]() ,
, ![]() .
.
![]()
![]()
![]()
![]()
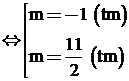 .
.
Vậy m = -1 hoặc thỏa yêu cầu đề bài.
Câu 42:
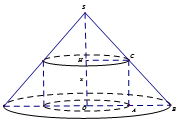
 Xem đáp án
Xem đáp án
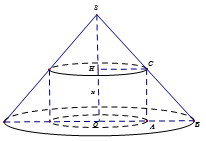
Ta có nên .
Suy ra thể tích khối trụ là:
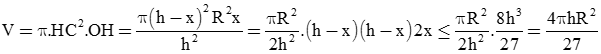
Do đó khối trụ lớn nhất bằng đạt được khi .
Vậy, thì khối trụ có thể tích lớn nhất.