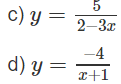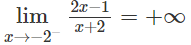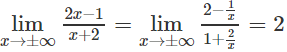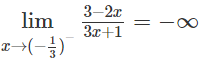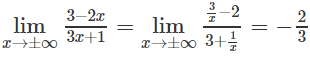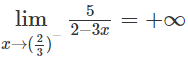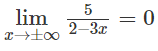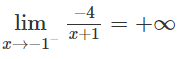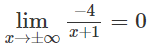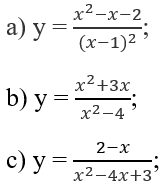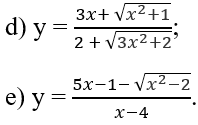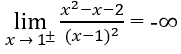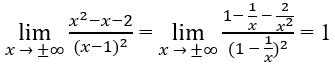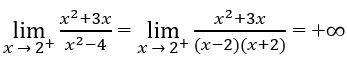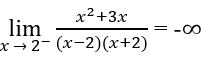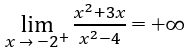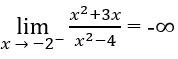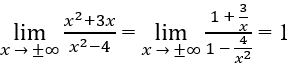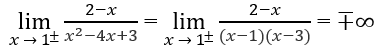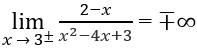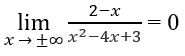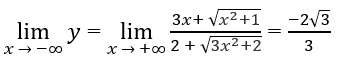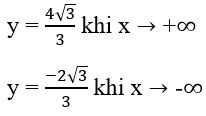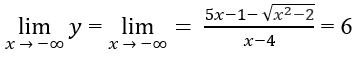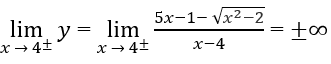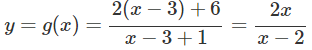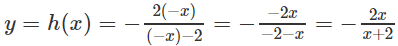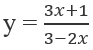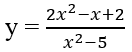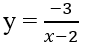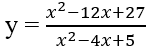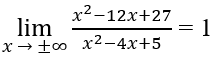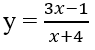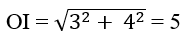Giải SBT Toán 12 Giải tích - Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Giải sbt Giải tích 12 Bài 4: Đường tiệm cận
-
1083 lượt thi
-
9 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm các tiệm cận đường và ngang của đồ thị mỗi hàm số sau:
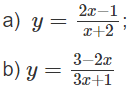
Xem đáp án
a) Ta có:
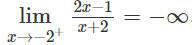
nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì
nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
b) Từ
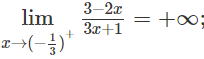
ta có x = là tiệm cận đứng
Vì
nên đường thẳng y = là tiệm cận ngang.
c) Vì
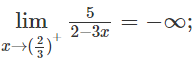
nên x = 2/3 là tiệm cận đứng.
Do
nên y = 0 là tiệm cận ngang.
d) Do
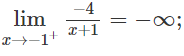
nên x = -1 là tiệm cận đứng.
Vì
nên y = 0 là tiệm cận ngang.
Câu 2:
Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau:
Xem đáp án
a) Vì
nên x = 1 là tiệm cận đứng.
Từ
Suy ra y = 1 là tiệm cận ngang.
b) Vì
và
nên x = 2 là một tiệm cận đứng.
Do
và
nên x = -2 là tiệm cận đứng thứ hai.
Ta lại có
nên y = a là tiệm cận ngang.
c) Do
nên x = 1 là tiệm cận đứng.
Mặt khác,
nên x = 3 cũng là tiệm cận đứng.
Vì
nên y = 0 là tiệm cận ngang.
d) TXĐ: R.
Từ
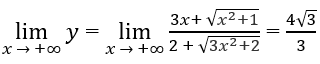
Ruy ra đồ thị hàm số có các tiệm cận ngang:
Đồ thị hàm số không có tiệm cận đứng.
e) TXĐ: D = (-∞; -√2) ∪ (√2;4) ∪ (4; +∞)
Do
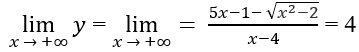
Cho nên đồ thị hàm số có hai tiệm cận ngang
y = 4 khi x ⇒ +∞
y = 6 khi x ⇒ -∞
Vì
Cho nên đường thẳng x = 4 là tiệm cận đứng của đồ thị hàm số.
Câu 3:
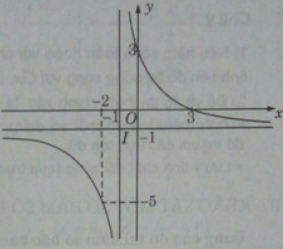
a) Cho hàm số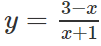 
có đồ thị (H)
Chỉ ra một phép biến hình biến (H) thành (H’) có tiệm cận ngang y = 2 và tiệm cận đứng x = 2.
b) Lấy đối xứng (H’) qua gốc (O), ta được hình (H’’). Viết phương trình của (H’’).
Xem đáp án
a) Từ đồ thị hàm số (H), để có hình (H’) nhận y = 2 là tiệm cận ngang và x = 2 là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị, sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương ứng sau:
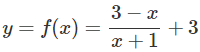
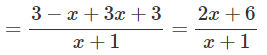
b) Lấy đối xứng hình (H’) qua gốc O, ta được hình (H’’) có phương trình là:
Câu 6:
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
Xem đáp án
Đáp án: A.
Nhận xét rằng hàm số dạng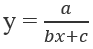 
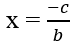
(a, b ≠ 0) có tiệm cận đứng là 
và tiệm cận ngang là y = 0.
Câu 7:
Tiệm cận ngang của đồ thị hàm số sau là:
Xem đáp án
Đáp án: A.
Vì x2 - 4x + 5 ≠ 0, ∀x nên tập xác định (-∞; +∞)
Vì
nên y = 1 là tiệm cận ngang.
Đồ thị hàm số không có tiệm cận đứng.
Câu 8:
Cho hàm số
Gọi I là giao điểm của hai tiệm cận. Tính OI.
Xem đáp án
Đáp án: C.
Vì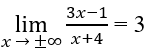 
nên y = 3 là tiệm cận ngang.
Vì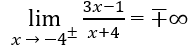 
nên x = -4 là tiệm cận đứng.
Câu 9:
Đồ thị hàm số nào sau đây có hai tiệm cận tạo với hai trục tọa độ một tứ giác có diện tích bằng 12?
Xem đáp án
Đáp án: D.
Tiệm cận đứng của đồ thị hàm số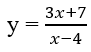 
là x = 4; tiệm cận ngang của đồ thị hàm số đó là y = 3. Diện tích hình chữ nhật tạo thành là
3 x 4 = 12.