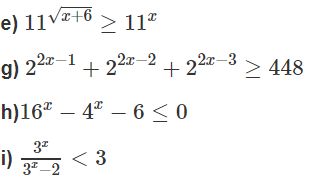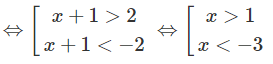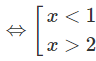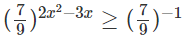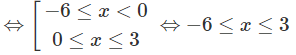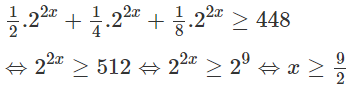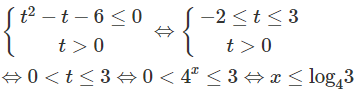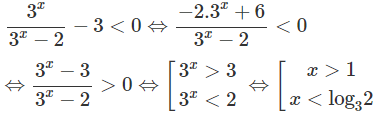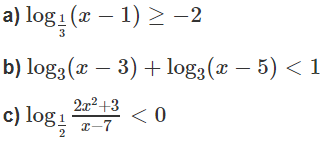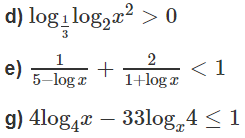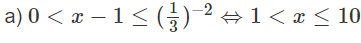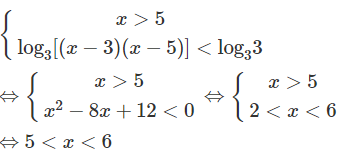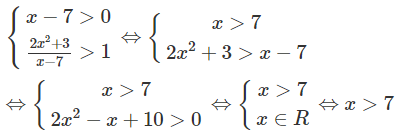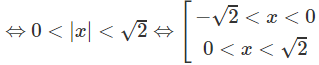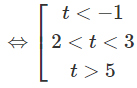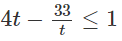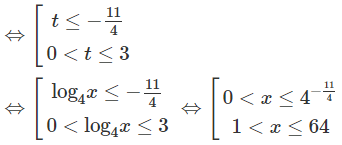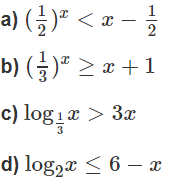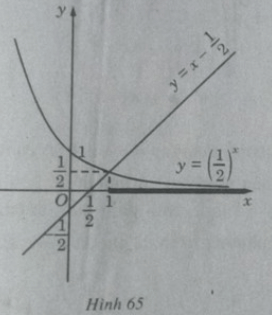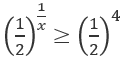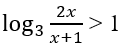Giải SBT Toán 12 Giải tích - Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit
Giải sbt Giải tích 12 Bài 6: Bất phương trình mũ và bất phương trình lôgarit
-
938 lượt thi
-
6 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Giải các bất phương trình mũ sau:
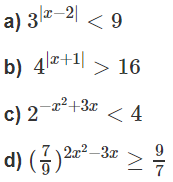
Xem đáp án
a) 3|x−2| < 32
⇔ |x − 2| < 2
⇔ −2 < x – 2 < 2
⇔ 0 < x < 4
b) 4|x+1| > 42
⇔ |x + 1| > 2
c) 2−x2 + 3x < 22
⇔ − x2 + 3x < 2
⇔ x2 − 3x + 2 > 0
d) 
⇔ 2x2 − 3x ≤ −1
⇔ 2x2 − 3x + 1 ≤ 0 ⇔ 12 ≤ x ≤ 1
e)
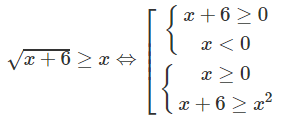
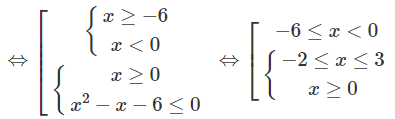
g)
h) Đặt t = 4x (t > 0), ta có hệ bất phương trình:
i)
Câu 2:
Giải các bất phương trình logarit sau:
Xem đáp án
b) 
c) 
d)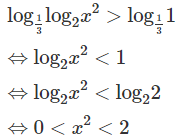 
e) Đặt t = logx với điều kiện t ≠ 5, t ≠ −1 ta có:
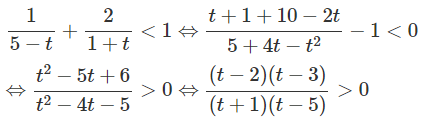
Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.
Vậy x < hoặc 100 < x < 1000 hoặc x > 100 000.
g) Với điều kiện x > 0, x ≠ 1 đặt t = log4x
ta có: 
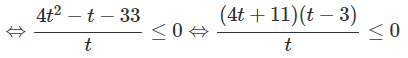
Câu 3:
Giải các bất phương trình sau bằng đồ thị:
Xem đáp án
a) Vẽ đồ thị của hàm số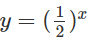 
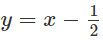
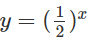
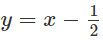
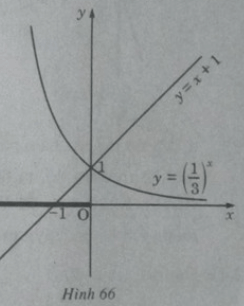
và đường thẳng
trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số
nằm phía dưới đường thẳng . Vậy tập nghiệm của bất phương trình đã cho là (1;+∞)
b) Vẽ đồ thị của hàm số 
và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
Khi x < 0 đồ thị của hàm số nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là (-∞;0]
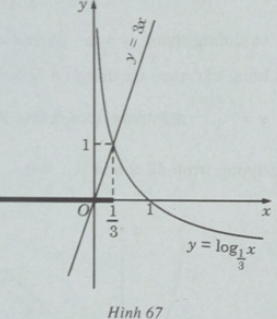
c) Vẽ đồ thị của hàm số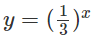 
và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ x = (H.67)
Khi x < 1/3 đồ thị của hàm số 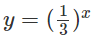nằm phía trên đường thẳng
y = 3x.
Vậy tập nghiệm của bất phương trình đã cho là (-∞;).
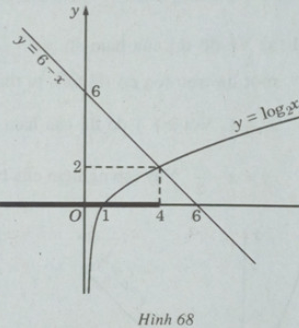
d) Vẽ đồ thị của hàm số y = log2x và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).
Khi x < 4, đồ thị của hàm số y = log2x nằm phía dưới y = 6 – x . Vậy tập nghiệm của bất phương trình đã cho là (-∞;4].
