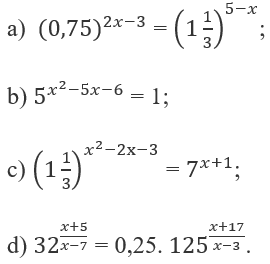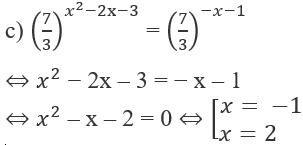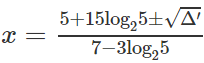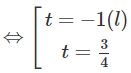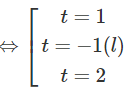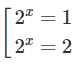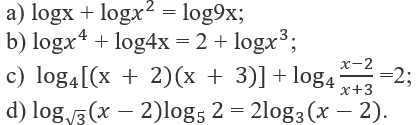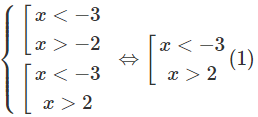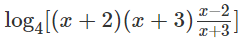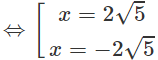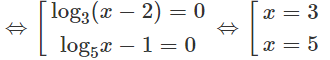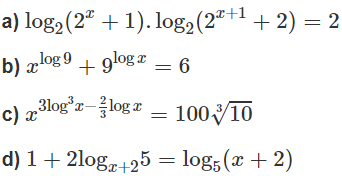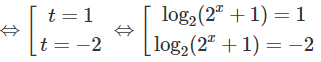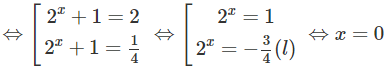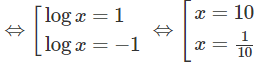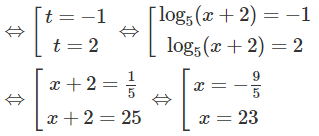Giải SBT Toán 12 Giải tích - Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit
Giải sbt Giải tích 12 Bài 5: Phương trình mũ và phương trình lôgarit
-
934 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Giải các phương trình mũ sau:
Xem đáp án
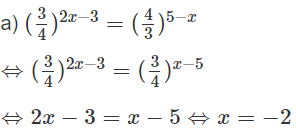
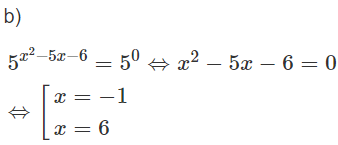
d) Hướng dẫn: Lấy logarit cơ số 2 cả hai vế
Phương trình đã cho có hai nghiệm phân biệt đều thỏa mãn điều kiện
Câu 2:
Giải các phương trình mũ sau:
a) 2x+4 + 2x+2 = 5x+1 + 3.5x;
b) 52x − 7x − 52x.17 + 7x.17 = 0;
c) 4.9x + 12x − 3.16x = 0;
d) −8x + 2.4x + 2x − 2 = 0.
Xem đáp án
a) 16.2x + 4.2x = 5.5x + 3.5x
⇔ 20.2x = 8.5x ⇔ (2/5)x = (2/5)1 ⇔ x = 1
b) 16.7x − 16.52x = 0
⇔ 7x = 52x ⇔ (7/25)x = (7/25)0 ⇔ x = 0
c) Chia hai vế cho 12x(12x > 0), ta được:
4(3/4)x + 1 − 3(4/3)x = 0
Đặt t = (3/4)x (t > 0), ta có phương trình:
4t + 1 − 3/t = 0 ⇔ 4t2 + t − 3 = 0
Do đó, (3/4)x = (3/4)1. Vậy x = 1.
d) Đặt t = 2x (t > 0), ta có phương trình:
−t3 + 2t2 + t – 2 = 0
⇔ (t − 1)(t + 1)(2 − t) = 0
Do đó: 
Câu 3:
Giải các phương trình logarit sau:
Xem đáp án
a) Với điều kiện x > 0, ta có
logx + 2logx = log9 + logx
⇔ logx = log3 ⇔ x = 3
b) Với điều kiện x > 0, ta có
4logx + log4 + logx = 2log10 + 3logx
⇔ logx = log5 ⇔ x = 5
c) Ta có điều kiện của phương trình đã cho là:
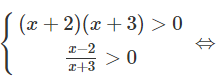
Khi đó, phương trình đã cho tương đương với:
= log416 ⇔ x2 − 4 = 16
Cả hai nghiệm trên đều thỏa mãn điều kiện (1).
d) Với điều kiện x > 2, ta có phương trình
Cả hai giá trị này đều thỏa mãn điều kiện x > 2.
Câu 4:
Xem đáp án
a) log2(2x + 1) .log2 [2(2x + 1)] = 2
⇔ log2 (2x + 1). [1 + log2 (2x + 1)] = 2
Đặt t = log2 (2x + 1), ta có phương trình
t(1 + t) = 2 ⇔ t2 + t – 2 = 0
b) Với điều kiện x >0, ta có: log(xlog9) = log(9logx)
log(xlog9) = log9.logx và log(9logx) = logx.log9
Nên log(xlog9) = log(9logx)
Suy ra: xlog9 = 9logx
Đặt t = xlog9, ta được phương trình 2t = 6 ⇔ t = 3 ⇔ xlog9 = 3
⇔ log(xlog9) = log3
⇔log9.logx = log3
⇔logx = log3/log9 ⇔ logx = 1/2
⇔ x = √10 (thỏa mãn điều kiện x > 0)
c) Với điều kiện x > 0, lấy logarit thập phân hai vế của phương trình đã cho, ta được:
(3log3x − 2logx/3).logx = 7/3
Đặt t = logx, ta được phương trình 3t4 − 2t2/3 – 7/3 = 0
⇔ 9t4 − 2t2 − 7 = 0
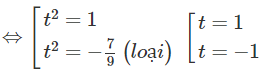
d) Đặt t = log5(x + 2) với điều kiện x + 2 > 0, x + 2 ≠ 1, ta có:
1 + 2/t = t ⇔ t2 – t – 2 = 0 , t ≠ 0
