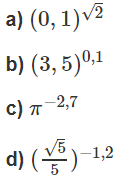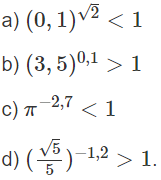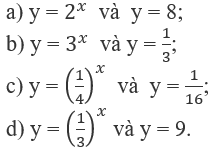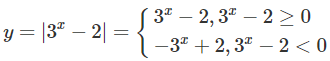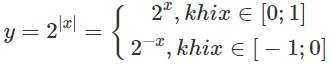Giải SBT Toán 12 Giải tích - Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit
Giải sbt Giải tích 12 Bài 4: Hàm số mũ. Hàm số lôgarit
-
939 lượt thi
-
19 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
Tìm tọa độ giao điểm của đồ thị của mỗi cặp hàm số sau:
Xem đáp án
a) (3; 8)
b) (−1; )
c) (2; )
d) (-2; 9).
Câu 3:
Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau:
a) (1,7)3 và 1;
b) (0,3)2 và 1;
c) (3,2)1,5 và (3,2)1,6;
d) (0,2)-3 và (0,2)-2;
e) ()√2 và ()1,4;
g) 6π và 63,14.
Xem đáp án
a) (1,7)3 > 1;
b) (0,3)2 < 1;
c) (3,2)1,5 < (3,2)1,6;
d) (0,2)-3 > (0,2)-2;
e) ()√2 < ()1,4;
g) 6π > 63,14.
Câu 4:
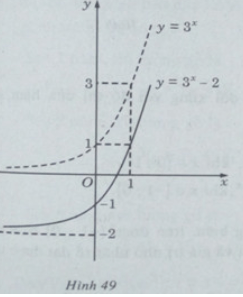
Từ đồ thị của hàm số y = 3x, hãy vẽ đồ thị của các hàm số sau:
a) y = 3x – 2
b) y = 3x + 2
c) y = |3x – 2|
d) y = 2 – 3x
Xem đáp án
a) Đồ thị của hàm số y: y = 3x − 2 nhận được từ đồ thị của hàm số y = 3x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
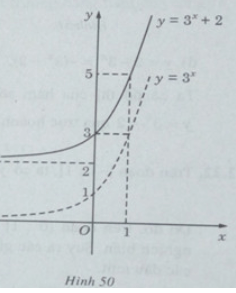
b) Đồ thị của hàm số y = 3x + 2 nhận được từ đồ thị của hàm số y = 3x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
c) 
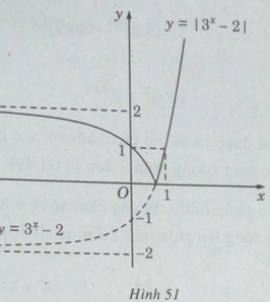
Do đó, đồ thị của hàm số y = |3x − 2| gồm:
- Phần đồ thị của hàm số y = 3x − 2 ứng với 3x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3x − 2 ứng với 3x – 2 < 0.
Vậy đồ thị của hàm số y = |3x − 2| có dạng như hình 51.
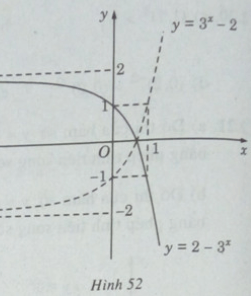
d) y = 2 – 3x = −(3x − 2)
Ta có đồ thị của hàm số y = 2 − 3x đối xứng với đồ thị cua hàm số y = 3x – 2 qua trục hoành (H.52).
Câu 5:
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 2|x| trên đoạn [-1; 1].
Xem đáp án
Trên đoạn [-1; 1], ta có :
y = log√5x
Do đó, trên đoạn [0;1] hàm số đồng biến, trên đoạn [-1;0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút.
Ta có: y(−1) = 2−(−1) = 21 = 2, y(0) = 20 = 1, y(1) = 21 = 2
Vậy max y = y(1) = y(−1) = 2, min y = y(0) = 1.
Câu 8:
Hãy so sánh x với 1, biết rằng:
a) log3x = −0,3;
b) = 1,7;
c) log2x = 1,3;
d) = −1,1.
Xem đáp án
a) x < 1
b) x < 1
c) x > 1
d) x > 1.
Câu 9:
Trong các hàm số sau, hàm số nào đồng biến?
Xem đáp án
Đáp án: D.
Vì hàm số đồng biến khi cơ số lớn hơn 1
Câu 10:
Trong các hàm số, hàm số nào nghịch biến?
Xem đáp án
Đáp án: B.
Vì hàm số nghịch biến khi cơ số nhỏ hơn 1
Câu 11:
Với giá trị nào của x thì đồ thị hàm số y = 4x nằm phía trên đường thẳng y = 1?
Xem đáp án
Đáp án A.