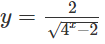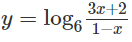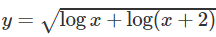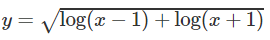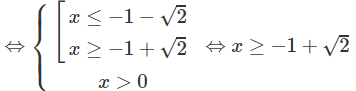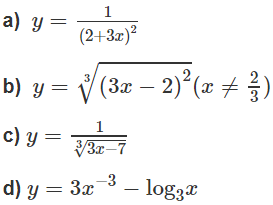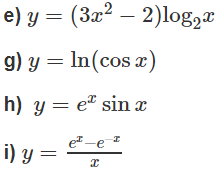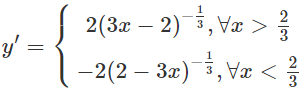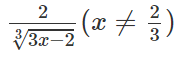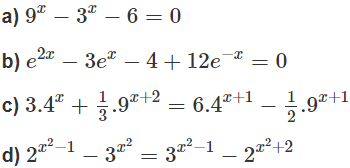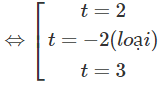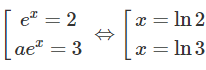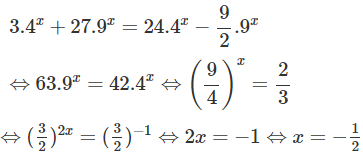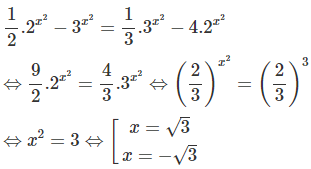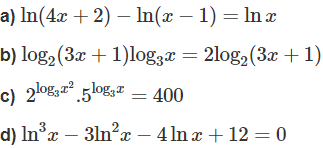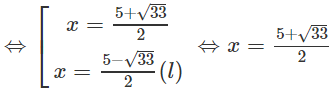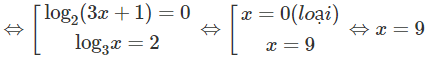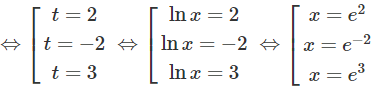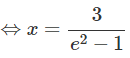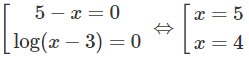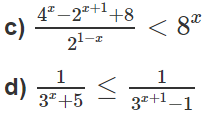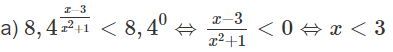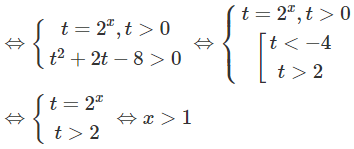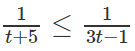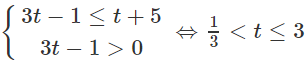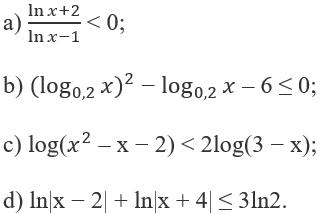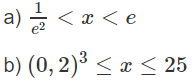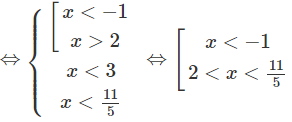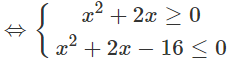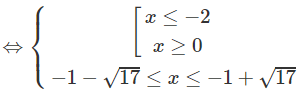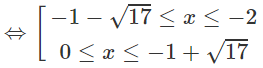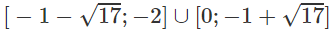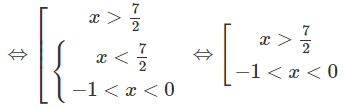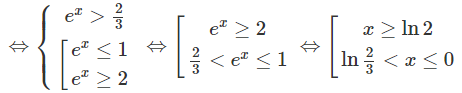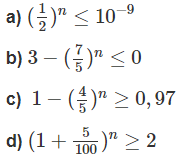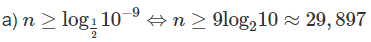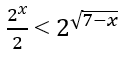26 câu hỏi trắc nghiệm thuộc Giải sbt Giải tích 12 Bài tập ôn tập chương 2

Câu 1:

Tìm tập xác định của các hàm số sau:

a)

b)

c)

d)

Xem đáp án

a) Hàm số xác định khi:

4x – 2 > 0 ⇔ 22x > 2 ⇔ x > $\frac{1}{2}$

Vậy tập xác định là D = ( $\frac{1}{2}$ ; +∞)

b) D = ( $- \frac{2}{3}$ ; 1)

c) logx + log(x + 2) ≥ 0

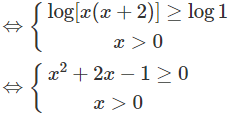
Vậy tập xác định là D = [−1 + √2; +∞)

d) Tương tự câu c, D = [√2; +∞).

Câu 2:

Tính đạo hàm của các hàm số sau:

Xem đáp án

a) y′ = −6(2 + 3x)−3

b)

y' =

Câu 3:

Giải các phương trình sau:

Xem đáp án

a) x = 1

b) Đặt t = ex (t > 0), ta có phương trình t2 − 3t – 4 + $\frac{12}{t}$ = 0 hay

t3 − 3t2 − 4t + 12 = 0

⇔ (t − 2)(t + 2)(t − 3) = 0

Do đó

c)

d)

Câu 4:

Giải các phương trình sau:

Xem đáp án

a) Với điều kiện x > 1 ta có phương trình:

ln(4x + 2) = ln[x(x − 1)]

⇔ 4x + 2 = x2 – x ⇔ x2 – 5x – 2 = 0

b) Với điều kiện x > 0, ta có phương trình

log2(3x + 1)[log3x − 2] = 0

c) Với điều kiện x > 0, ta có phương trình:

4log3x. 5log3x = 400

⇔ 20log3x = 202

⇔ log3x = 2 ⇔ x = 9 (thỏa mãn điều kiện)

d) Đặt t = lnx(x > 0), ta có phương trình:

t3 – 3t2 – 4t + 12 = 0 ⇔ (t – 2)(t + 2)(t – 3) = 0

Câu 5:

Giải các phương trình sau:

a) e2+lnx = x + 3;

b) e4−lnx = x;

c) (5 − x).log(x − 3) = 0

Xem đáp án

a) Với điều kiện x > 0, ta có phương trình

e2. elnx = x + 3

⇔ e2.x = x + 3

⇔x(e2 − 1) = 3

(thỏa mãn điều kiện)

b) Tương tự câu a), x = e2

c) Với điều kiện x > 3 ta có:

Câu 6:

Giải các bất phương trình mũ sau:

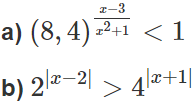
Xem đáp án

b) 2|x − 2| > 22|x+1|

⇔ |x−2| > 2|x+1|

⇔ x2 − 4x + 4 > 4(x2 + 2x + 1)

⇔ 3x2 + 12x < 0

⇔ −4 < x < 0

c) 22x − 2.2x + 8 < 23x. 21−x

⇔ 22x + 2.2x − 8 > 0

d) Đặt t = 3x (t > 0) , ta có bất phương trình

Vì vế trái dương nên vế phải cũng phải dương, tức là 3t - 1 > 0.

Từ đó ta có hệ:

Do đó 1/3 < 3x ≤ 3. Vậy −1 < x ≤ 1.

Câu 7:

Giải các bất phương trình lôgarit sau:

Xem đáp án

c) Bất phương trình đã cho tương đương với hệ:

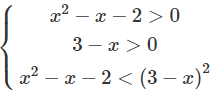
Vậy tập nghiệm là (−∞; −1) ∪ (2; 11/5)

d) ln|(x − 2)(x + 4)| ≤ ln8

⇔|x2 + 2x − 8| ≤ 8

⇔ −8 ≤ x2 + 2x – 8 ≤ 8

Vậy tập nghiệm là

Câu 8:

Giải các bất phương trình sau:

a) (2x − 7)ln(x + 1) > 0;

b) (x − 5)(logx + 1) < 0;

c) 2log32x + 5log22 + log2x – 2 ≥ 0

d) ln(3ex − 2) ≤ 2x

Xem đáp án

a) Bất phương trình đã cho tương đương với hệ sau:

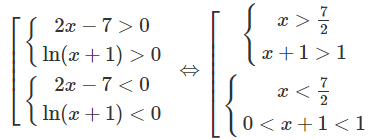
Vậy tập nghiệm là (−1;0) ∪ ( $\frac{7}{2}$ ; +∞)

b) Tươngg tự câu a), tập nghiệm là ( $\frac{1}{10}$ ; 5)

c) Đặt t = log2x, ta có bất phương trình 2t3 + 5t2 + t – 2 ≥ 0 hay (t + 2)(2t2 + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ $\frac{1}{2}$

Suy ra $\frac{1}{4}$ ≤ x ≤ $\frac{1}{2}$ hoặc x ≥ √2

Vậy tập nghiệm của bất phương trình đã cho là: [ $\frac{1}{4}$ ; $\frac{1}{2}$ ] ∪ [√2; +∞)

d) Bất phương trình đã cho tương đương với hệ:

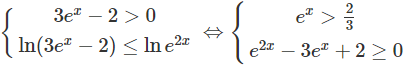
Vậy tập nghiệm là (ln( $\frac{2}{3}$ ); 0] ∪ [ln2; +∞)

Câu 9:

số tự nhiên n bé nhất sao cho:

Xem đáp án

Vì n là số tự nhiên bé nhất nên n = 30.

b) n = 4

c) n = 16

d) n = 15

Câu 10:

Nếu $a^{\frac{\sqrt{3}}{3}}$ > $a^{\frac{\sqrt{2}}{2}}$ và logb( $\frac{3}{4}$ ) < logb( $\frac{4}{5}$ ) thì:

A. 0 < a < 1, b > 1

B. 0 < a < 1, 0 < b < 1

C. a > 1, b > 1

D. a > 1, 0 < b < 1

Xem đáp án

Đáp án A.

Câu 11:

Hàm số y = x2e-x tăng trong khoảng:

A. (-∞;0)

B. (2; +∞)

C. (0;2)

D. (-∞; +∞)

Xem đáp án

Đáp án C.

Câu 12:

Hàm số y = ln(x2 - 2mx + 4) có tập xác định D = R khi:

A. m = 2

B. m > 2 hoặc m < -2

C. m < 2

D. -2 < m < 2

Xem đáp án

Đáp án D.

Câu 13:

Đạo hàm của hàm số y = x(lnx - 1) là:

A. lnx - 1

B. lnx

C. ( $\frac{1}{x}$ ) - 1

D. 1

Xem đáp án

Đáp án B.

Câu 14:

Nghiệm của phương trình log2(log4x) = 1 là:

A. 2

B. 4

C. 8

D. 16

Xem đáp án

Đáp án D.

Câu 15:

Nghiệm của bất phương trình log2(3x - 2) < 0 là:

A. x > 1

B. x < 1

C. 0 < x < 1

D. $\log_{3} 2$ < x < 1

Xem đáp án

Đáp án D.

Câu 16:

Tập nghiệm của bất phương trình 3x ≥ 5 - 2x là:

A. [1; +∞)

B. (-∞;1]

C. (1; +∞)

D. ∅

Xem đáp án

Đáp án A.

Hướng dẫn: Giải bằng đồ thị.

Câu 17:

Cho hàm số: 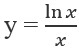Chọn khẳng định đúng.

A. Hàm số có một cực tiểu

B. Hàm số có một cực đại

C. Hàm số không có cực trị

D. Hàm số có một cực đại và một cực tiểu

Xem đáp án

Đâp án B.

Hướng dẫn: Tính đạo hàm và lập bảng biến thiên.

Câu 18:

Phương trình 3x2 - 2x + 1 = 1 có nghiệm là

A. x = 1

B. x = 0

C. x = -1

D. x = $\frac{1}{3}$

Xem đáp án

Đáp án A.

Câu 19:

Tìm tập hợp nghiệm của phương trình 2x2 - x - 4 = 0

A. {1;2}

B. {2;3}

C. {-2;3}

D. {2;-3}

Xem đáp án

Đáp án C.

Câu 20:

Tìm tập hợp nghiệm của phương trình xlg4 + 4lgx = 32

A. {100}

B. {10}

C. {100;10}

D. {4}

Xem đáp án

Đáp án A.

Câu 21:

Tìm tập hợp nghiệm của phương trình log₂x + log2(x - 1) = 1

A. {1}

B. {2}

C. {1;2}

D. {-1;2}

Xem đáp án

Đáp án B.

Câu 22:

Số nghiệm của phương trình log(x2 - 6x + 7) = log(x - 3) là

A. 2

B. 1

C. 0

D. Vô số

Xem đáp án

Đáp án B.

Câu 23:

Tìm tập hợp nghiệm của phương trình sau:

A. {2}

B. { $\frac{1}{4}$ }

C. {2; $\frac{1}{4}$ }

D. {2; $\frac{1}{16}$ }

Xem đáp án

Đáp án D.

Câu 24:

Tìm tập nghiệm của bất phương trình:

A. x > $\frac{3}{2}$

B. x < $\frac{3}{2}$

C. x > $\frac{2}{3}$

D. x < $\frac{2}{3}$

Xem đáp án

Đáp án A.

Câu 25:

Tìm tập nghiệm của bất phương trình:

A. x < 3

B. x ≥ 1

C. 1 ≤ x < 3

D. x < 1

Xem đáp án

Đáp án A.

Câu 26:

Tìm x, biết ${(\sqrt{2})}^{x} = \sqrt[3]{2}$

A. x = 3

B. x = $\frac{3}{2}$

C. x = $\frac{2}{3}$

D. x = $\frac{1}{6}$

Xem đáp án

Đáp án C.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Giải SBT Toán 12 Giải tích - Chương 2: Hàm số lũy thừa. Hàm số mũ và hàm số logarit

Giải sbt Giải tích 12 Bài tập ôn tập chương 2

Danh sách câu hỏi

Bài thi liên quan