10 câu hỏi trắc nghiệm thuộc Đề kiểm tra 15 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 1)

Top 8 Đề kiểm tra Toán 12 Chương 1 Giải tích có đáp án

Đề kiểm tra 15 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 1)

1543 lượt thi
10 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho hàm số $y = \frac{x + 1}{1 - x}$ . Khẳng định nào sao đây là khẳng đinh đúng?

A. Hàm số nghịch biến trên khoảng $(- \infty; 1) \cup (1; + \infty)$

B. Hàm số đồng biến trên khoảng $(- \infty; - 1) \cup (1; + \infty)$

C. Hàm số nghịch biến trên các khoảng $(- \infty; 1) v à (1; + \infty)$

D. Hàm số đồng biến trên các khoảng $(- \infty; 1) v à (1; + \infty)$

Xem đáp án

Chọn D.

Hàm số đồng biến trên các khoảng $(- \infty; 1) v à (1; + \infty)$

Câu 2:

Cho hàm số $y = - x^{3} + 3 x^{2} - 3 x + 2$ Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên R.

B. Hàm số nghịch biến trên các khoảng $(- \infty; 1)$ và $(1; + \infty)$

C. Hàm số đồng biến trên khoảng $(- \infty; - 1)$ và nghịch biến trên khoảng $(1; + \infty)$

D. Hàm số luôn đồng biến trên R.

Xem đáp án

Chọn A

TXĐ: D = R.

Ta có y' = -3x2 + 6x - 3 = -3(x - 1)2 ≤ 0, ∀ x ∈ R

Do đó, hàm số luôn nghịch biến trên R.

Câu 3:

Hỏi hàm số $y = \frac{x^{2} - 3 x + 5}{x + 1}$ nghịch biến trên các khoảng nào ?

A. $(- \infty; - 4) v à (2; + \infty)$

B. (-4;2)

C. $(- \infty; - 1) v à (- 1; + \infty)$

D. (-4;-1) và (-1;2)

Xem đáp án

Chọn D.

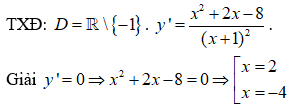
y' không xác định khi x = -1 . Bảng biến thiên:

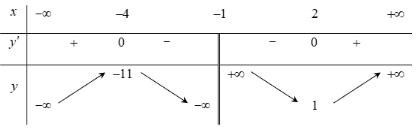
Hàm số nghịch biến trên các khoảng (-4;-1) và (-1;2)

Câu 4:

Biết đồ thị hàm số $y = x^{3} - 3 x + 1$ có hai điểm cực trị A, B . Khi đó phương trình đường thẳng AB là:

A. y = x-2

B. y = 2x - 1

C. y = -2x + 1

D. y = -x + 2

Xem đáp án

Chọn C

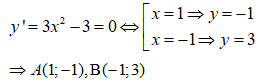
Đường thẳng AB qua A(1; -1) và có vecto chỉ phương $\vec{A B} (- 2; 4)$ suy ra 1 vecto pháp tuyến là $\vec{n} (2; 1)$

Phương trình đường thẳng AB là:

2(x - 1) + 1.(y + 1) = 0 hay 2x + y - 1 = 0

Câu 5:

Tìm tất cả các giá trị của tham số m để hàm số $y = x^{3} - m x^{2} + (2 m - 3) x - 3$ đạt cực đại tại x = 1.

A. m = 3

B. m > 3

C. m ≤ 3

D. m < 3

Xem đáp án

Chọn B.

Đạo hàm: y’ = 3x2 – 2mx + 2m – 3 và y” = 6x – 2m

+ Để hàm số đạt cực đại x = 1 thì:

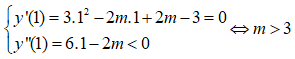
Câu 6:

Cho hàm số $y = x^{3} - 3 x^{2} + 2$ . Khẳng định nào sau đây là đúng?

A. Hàm số đạt cực đại tại $x = 2$ và đạt cực tiểu tại $x = 0$

B. Hàm số đạt cực tiểu tại $x = 2$ và đạt cực đại $x = 0$

C. Hàm số đạt cực đại tại $x = - 2$ và cực tiểu tại $x = 0$ .

D. Hàm số đạt cực đại tại $x = 0$ và cực tiểu tại $x = - 2$

Xem đáp án

Chọn B.

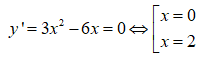
Lập bảng biến thiên ta được hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2.

Câu 7:

Cho hàm số $y = x^{4} - 2 x^{2} + 3$ . Khẳng định nào sau đây là đúng?

A. Hàm số có ba điểm cực trị.

B. Hàm số chỉ có đúng 2 điểm cực trị.

C. Hàm số không có cực trị.

D. Hàm số chỉ có đúng một điểm cực trị.

Xem đáp án

Chọn B.

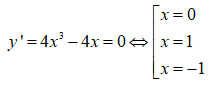
y(0) = 3; y(1)= y(-1) = 2 nên hàm số có hai cực trị.

Câu 8:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = \frac{x - m + 2}{x + 1}$ giảm trên các khoảng mà nó xác định ?

A. m < 1

B. m ≤ -3

C. m ≤ 1

D. m < -3

Xem đáp án

Chọn A

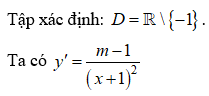
Để hàm số giảm trên các khoảng mà nó xác định

Câu 9:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên R?

$y = - \frac{1}{3} x^{3} - m x^{2} + (2 m - 3) x - m + 2$

A. -3 ≤ m ≤1.

B. m ≤ 1.

C. -3 < m < 1.

D. m ≤ -3; m ≥ 1.

Xem đáp án

Chọn A.

Tập xác định: D = R.

Ta có

Để hàm số nghịch biến trên R thì

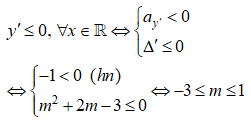
Câu 10:

Tìm số nguyên m nhỏ nhất sao cho hàm số $y = \frac{(m + 3) x - 2}{x + m}$ luôn nghịch biến trên các khoảng xác định của nó?

A. m = -1

B. m = -2

C. m = 0

D. Không có m

Xem đáp án

Chọn D.

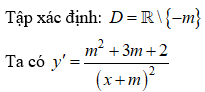
Để hàm số đã cho nghịch biến trên khoảng xác định:

⇔ y' < 0, ∀ x ∈ D ⇔ m2 + 3m + 2 < 0 ⇔ -2 < m < -1

Vậy không có số nguyên m nào thuộc khoảng (-2;-1).

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 8 Đề kiểm tra Toán 12 Chương 1 Giải tích có đáp án

Đề kiểm tra 15 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 1)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương