Đề kiểm tra 15 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 3)
-
1605 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
Xem đáp án
Chọn A
Ta có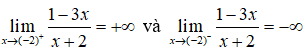 
nên đồ thị hàm số có tiệm cận đứng là x = -2
Ta có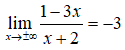 
nên đồ thị hàm số có tiệm cận ngang là y = -3
Câu 2:
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
Xem đáp án
Chọn A
Ta có: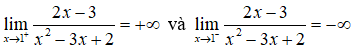 
nên đồ thị hàm số có tiệm cận đứng là x = 1
Tương tự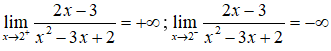 
nên đồ thị hàm số có tiệm cận đứng là x = 2
Ta có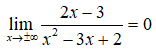 
nên đồ thị hàm số có tiệm cận ngang là y = 0
Câu 3:
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
Xem đáp án
Chọn A
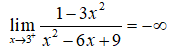
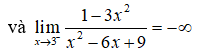
nên đồ thị hàm số có tiệm cận đứng là x = 3.
Ta có
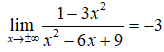
nên đồ thị hàm số có tiệm cận ngang là y = -3
Câu 4:
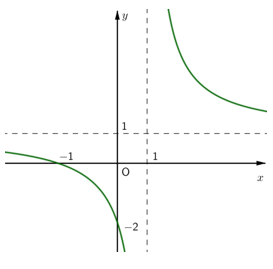
Đồ thị như hình vẽ là của hàm số nào sau đây :
Xem đáp án
Chọn C
Từ đồ thị ta thấy có tiệm cận đứng là x = 1 và y = 1 → loại A,B
Xét tiếp thấy giao điểm của đồ thị hàm số với trục tung là (0; -2) → chọn C.
Câu 5:
Cho hàm số có đồ thị (C). Kết luận nào sau đây đúng ?
Xem đáp án
Chọn C
Xét phương trình: mx + 9 = 0.
Với x = -m ta có: -m2 + 9 = 0 ⇔ m = ±3
Kiểm tra thấy với m = ±3 thì hàm số không có tiệm cận đứng và tiệm cận ngang.
Khi m = ±3 hàm số luôn có tiệm cận đứng x = m hoặc x = -m và tiệm cận ngang y = m
Câu 6:
Tìm tất cả các đường tiệm cận của đồ thị hàm số
Xem đáp án
Chọn A
Vì TXĐ của hàm số là R nên đồ thị hàm số không có tiệm cận đứng.
Vậy đồ thị hàm số có hai đường tiệm cận ngang là y = ±1
Câu 7:
Với giá trị nào của m thì đồ thị tiệm cận đứng đi qua điểm
Xem đáp án
Chọn D
Để đồ thị hàm số có đường tiệm cận đứng thì m2 + 2 ≠ 0 luôn đúng với mọi m.
Khi đó đồ thị hàm số có đường tiệm cận đứng là
Vậy để tiệm cận đứng đi qua điểm
Câu 8:
Xác định m để đồ thị hàm số có đúng hai tiệm cận đứng.
Xem đáp án
Chọn D
Đồ thị hàm số 
có đúng hai tiệm cận đứng
⇔ phương trình 
có hai nghiệm phân biệt
