Đề kiểm tra 15 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 4)
-
1968 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Đường thẳng cắt đồ thị hàm số tại các điểm có tọa độ là
 Xem đáp án
Xem đáp án
Chọn C.
Phương trình hoành độ giao điểm :
![]()
![]()
Thế vào phương trình y = x - 1 được tung độ tương ứng 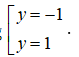
Vậy đường thẳng cắt đồ thị tại hai điểm là: (0;-1), (2;1)
Câu 2:
Cho hàm số . Phương trình tiếp tuyến của đồ thị (C) tại điểm M(1; 4) là
 Xem đáp án
Xem đáp án
Chọn D
Ta có y' = 3x2 + 6x ⇒ k = y'(1) = 9.
Phương trình tiếp tuyến tại M(1;4) là
d: y = y'(x0)(x - x0) + y0 = 9(x - 1) + 4 = 9x - 5.
Câu 3:
Cho hàm số . Phương trình tiếp tuyến của (C) tại điểm M thuộc (C) và có hoành độ bằng
 Xem đáp án
Xem đáp án
Chọn A.
Ta có y' = -6x2 + 12x.
Với x0 = 3 ⇒ y0 = -5 ⇒ M(3;-5) và hệ số góc k = y^' (3) = -18.
Vậy phương trình tiếp tuyến tại là y = -18(x - 3)-5 = -18x + 49.
Câu 4:
Đồ thị hàm số cắt đường thẳng y = m tại ba điểm phân biệt thì tất cả các giá trị tham số m thỏa mãn là
 Xem đáp án
Xem đáp án
Chọn C.
Phương trình hoành độ giao điểm: x3 - 3x2 + 1 = m
Ta có: y' = 3x2 - 6x; y' = 0 ⇔ x = 0 ∨ x = 2.
Bảng biến thiên:
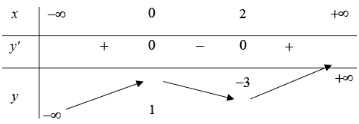
Do đó, đồ thị cắt đường thẳng y = m tại ba điểm phân biệt khi – 3 < m < 1.
Vậy chọn – 3 < m < 1.
Câu 5:
Cho hàm số có đồ thị (C). Từ điểm M(1;3) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?
 Xem đáp án
Xem đáp án
Chọn C.
Đường thẳng đi qua M(1;3) có hệ số góc k có dạng d: y = k(x - 1) + 3.
d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm
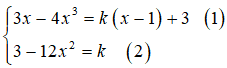
Thay (2) vào (1) ta được
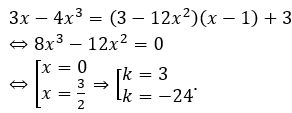
Vậy có 2 tiếp tuyến
Câu 6:
Cho hàm số . Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt là
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm: -x4 + 2x2 + m = 0 ⇔ m = x4 - 2x2.
Đặt (C): y = x4 - 2x2 và d: y = m
Xét hàm số y = x4 - 2x2.
Ta có y' = 4x3 - 4x; y' = 0 ⇔ x = 0 ∨ x = -1 ∨ x = 1.
Bảng biến thiên:
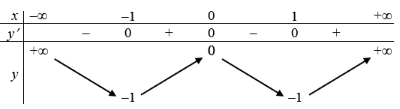
Đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt khi -1 < m < 0.
Vậy chọn -1 < m < 0a
Câu 7:
Cho hàm số Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt là
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm:
![]()
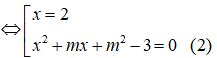
Để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt ⇔ Phương trình (1) có ba nghiệm phân biệt ⇔ Phương trình (2) có hai nghiệm phân biệt khác 2
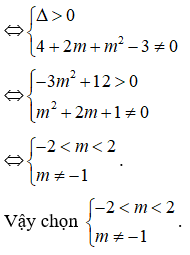
Câu 8:
Cho hàm số và đường thẳngTập tất cả các giá trị của tham số m sao cho (C) và d cắt nhau tại hai điểm phân biệt là
 Xem đáp án
Xem đáp án
Chọn C.
Phương trình hoành độ giao điểm của đồ thị (c) và đường thẳng d:
![]()
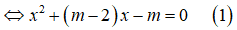
(C) cắt d tại hai điểm phân biệt ⇔(1) có hai nghiệm phân biệt
![]()
Vậy d luôn cắt (C) tại 2 điểm phân biệt.
