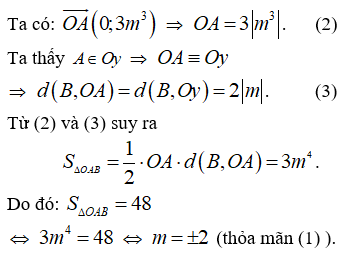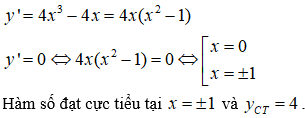20 câu hỏi trắc nghiệm thuộc Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 4)

Câu 1:

Cho hàm số $y = \frac{3 x - 1}{- 4 + 2 x}$ Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số nghịch biến trên R

B. Hàm số luôn nghịch biến trên từng khoảng xác định.

C. Hàm số đồng biến trên các khoảng $(- \infty; 2) v à (2; + \infty)$

D. Hàm số nghịch biến trên các khoảng $(- \infty; - 2) v à (2; + \infty)$

Xem đáp án

Chọn B.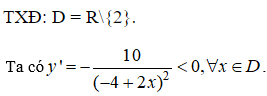

Do đó, hàm số đã cho nghịch biến trên từng khoảng xác định.

Câu 2:

Cho hàm số $y = x^{3} - 3 x^{2} + 2 .$ Khẳng định nào sau đây là đúng?

A. Hàm số đạt cực đại tại x =2 và đạt cực tiểu tại x = 0.

B. Hàm số đạt cực tiểu tại x = 2 và đạt cực đại x = 0.

C. Hàm số đạt cực đại tại x = -2 và cực tiểu tại x = 0.

D. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = - 2.

Xem đáp án

Chọn B

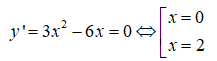
Lập bảng biến thiên ta được hàm số đạt cực đại tại x= 0 và đạt cực tiểu tại x= 2

Câu 3:

Giá trị nhỏ nhất của hàm số $f (x) = \frac{x^{2} - x + 1}{x - 1}$ trên khoảng (1;+∞) là:

A. $\underset{(1; + \infty)}{m i n} y = - 1$

B. $\underset{(1; + \infty)}{m i n} y = 3$

C. $\underset{(1; + \infty)}{m i n} y = 5$

D. $\underset{(1; + \infty)}{m i n} y = - \frac{7}{3}$

Xem đáp án

Chọn B.

Hàm số xác định với ∀ x ∈ (1;+∞)

Nhận xét: Hàm số f(x) liên tục trên (1;+∞)

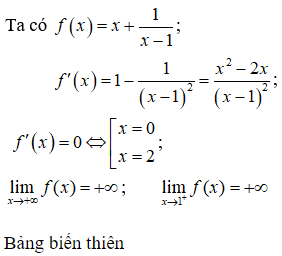
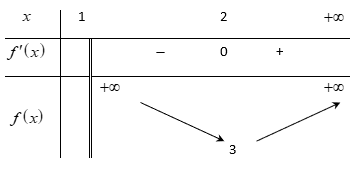
Từ bảng biến thiên ta có:

Câu 4:

Cho hàm số $y = - x^{3} + 3 x^{2} - 3 x + 2$ . Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số luôn nghịch biến trên R.

B. Hàm số nghịch biến trên các khoảng $(- \infty; 1)$ và $(1; + \infty)$

C. Hàm số đồng biến trên khoảng $(- \infty; 1)$ và nghịch biến trên khoảng $(1; + \infty)$

D. Hàm số luôn đồng biến trên R.

Xem đáp án

Chọn A.

TXĐ: D = R.

Do đó, hàm số đã cho nghịch biến trên R.

Câu 5:

Giá trị cực tiểu của hàm số $y = x^{4} - 2 x^{2} + 5$ là:

A. 5

B. 4

C. 0

D. 1

Xem đáp án

Chọn B

Câu 6:

Hàm số $y = \sin x + 1$ đạt giá trị lớn nhất trên đoạn $[- \frac{π}{2}; \frac{π}{2}]$ bằng:

A. 2

B. $\frac{π}{2}$

C. 0

D. 1

Xem đáp án

Chọn A.

TXĐ: D = R.

Câu 7:

Số đường tiệm cận của đồ thị hàm số $y = \frac{x + 1}{x^{2} - 4}$ là:

A. 4

B. 2.

C. 1.

D. 3.

Xem đáp án

Chọn D

Tiệm cận đứng là x = ±2 và tiệm cận ngang là y = 0

→ Số đường tiệm cận là 3

Câu 8:

Số tiệm cận của hàm số $y = \frac{\sqrt{x^{2} + 1} - x}{\sqrt{x^{2} - 9} - 4}$ là

A. 2

B. 4

C. .3

D. 1

Xem đáp án

Chọn B

Điều kiện xác định

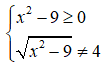
Khi đó có

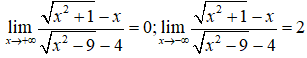
nên đồ thị hàm số có hai đường tiệm cận ngang.

Mặt khác có

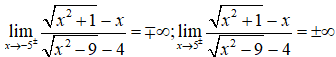
nên đồ thị hàm số có hai đường tiệm cận đứng.

Vậy đồ thị hàm số đã cho có 4 đường tiệm cận.

Câu 9:

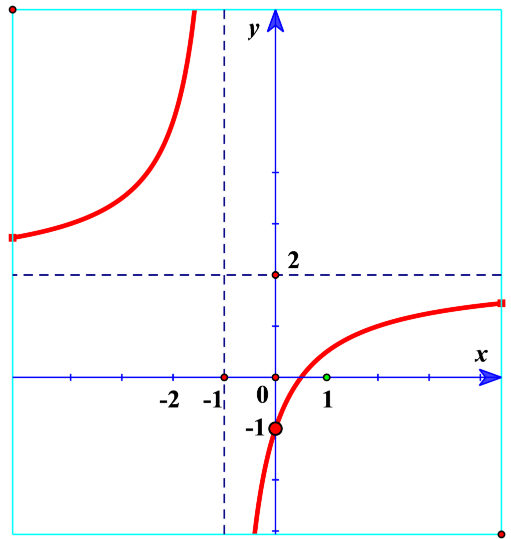
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. $y = \frac{2 x - 1}{x + 1}$

B. $y = \frac{2 x + 1}{x - 1}$

C. $y = \frac{2 x + 1}{x + 1}$

D. $y = \frac{1 - 2 x}{x - 1}$

Xem đáp án

Chọn A.

Nhìn vào đồ thị ta thấy ngay tiệm cận đứng x = -1, tiệm cận ngang y = 2. Loại B, D.

Đồ thị hàm số đi qua điểm (0;-1).

Loại đáp án B

Chọn đáp án A

Câu 10:

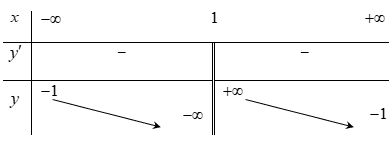
Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. $y = \frac{x + 3}{x - 1}$

B. $y = \frac{- x - 2}{x - 1}$

C. $y = \frac{- x + 3}{x - 1}$

D. $y = \frac{- x - 3}{x - 1}$

Xem đáp án

Chọn C.

Nhìn vào bảng biến thiên ta thấy ngay tiệm cận đứng x = 1 , tiệm cận ngang y = -1. suy ra loại đáp án A.

Nhìn vào bảng biến thiên, hàm số nghịch biến trên các khoảng

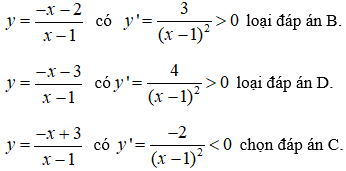
Câu 11:

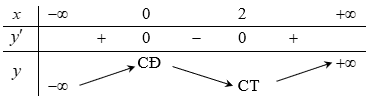
Bảng biến thiên sau đây là của một trong 4 hàm số được liệt kê dưới đây. Hỏi đó là hàm số nào?

A. $y = - x^{3} - 3 x^{2} + 2$

B. $y = x^{3} - 3 x^{2} + 2$

C. $y = x^{3} + 3 x^{2} - 2$

D. $y = - x^{3} + 3 x^{2} + 2$

Xem đáp án

Chọn B.

Dựa vào bảng biến thiên ta thấy hệ số a > 0 nên ta loại phương án A và D.

Phương trình y’ = 0 có hai nghiệm là x = 0 hoặc x = 2 nên chỉ có phương án B là phù hợp.

Câu 12:

Cho hàm số $y = \sqrt{3 x^{2} - x^{3}}$ . Khẳng định nào sau đây là khẳng định sai?

A. Hàm số đồng biến trên khoảng (0;2)

B. Hàm số đồng biến trên các khoảng $(- \infty; 0); (2; 3)$

C. Hàm số nghịch biến trên các khoảng $(- \infty; 0); (2; 3)$

D. Hàm số nghịch biến trên khoảng (2;3)

Xem đáp án

Chọn B.

Điều kiện xác định:

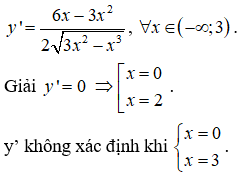
Bảng biến thiên:

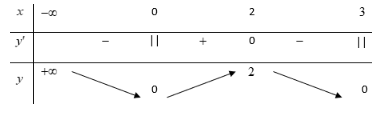
Hàm số nghịch biến (-∞;0) và (2;3). Hàm số đồng biến (0;2).

Câu 13:

ho hàm số $y = \sqrt{x^{2} - 2 x}$ . Khẳng định nào sau đây là đúng

A. Hàm số có hai điểm cực trị.

B. Hàm số đạt cực tiểu tại x = 0.

C. Hàm số đạt cực đại x = 2.

D. Hàm số không có cực trị.

Xem đáp án

Chọn D

TXĐ: D = (-∞;0] ∪ [2;+∞).

y’ không đổi dấu trên các khoảng xác định nên hàm số không có cực trị.

Câu 14:

Đường thẳng $y = x - 1$ cắt đồ thị hàm số $y = \frac{2 x - 1}{x + 1}$ tại các điểm có tọa độ là

A. (0; 2)

B. (-1; 0); (2; 1)

C. (0; -1); (2; 1)

D. (1; 2)

Xem đáp án

Chọn C

Phương trình hoành độ giao điểm của 2 đồ thị hàm số:

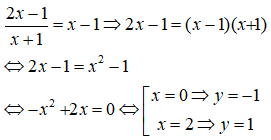
Vậy đường thẳng d cắt đồ thị hàm số (C) tại 2 điểm phân biệt là ( 0; -1) và (2;1).

Câu 15:

Xác định m để đồ thị hàm số $y = \frac{3}{4 x^{2} + 2 (2 m + 3) x + m^{2} - 1}$ có đúng hai tiệm cận đứng.

A. $m < - \frac{13}{12}$

B. -1 < m < 1

C. $m > - \frac{3}{2}$

D. $m > - \frac{13}{12}$

Xem đáp án

Chọn D

Đồ thị hàm số

có đúng hai tiệm cận đứng

⇔ phương trình có hai nghiệm phân biệt

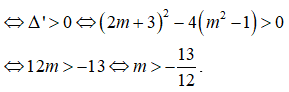
Câu 16:

Cho hàm số $y = (m - 1) x^{3} - 3 x^{2} - (m + 1) x + 3 m^{2} - m + 2$ . Để hàm số có cực đại, cực tiểu thì:

A. m = 1

B. m ≠ 1

C. m > 1

D. m tùy ý.

Xem đáp án

Chọn B

Để hàm số có cực đại, cực tiểu thì phương trình (*) có 2 nghiệm phân biệt:

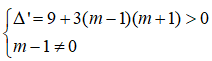
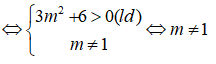
Câu 17:

Cho hàm số $y = a x^{3} + b x^{2} + c x + d .$ Nếu đồ thị hàm số có 2 điểm cực trị là gốc tọa độ và điểm A(-1; -1) thì hàm số có phương trình là:

A. $y' = 2 x^{3} - 3 x^{2}$

B. $y' = - 2 x^{3} - 3 x^{2}$

C. $y' = x^{3} + 3 x^{2} + 3 x$

D. $y' = x^{3} - 3 x - 1$

Xem đáp án

Chọn B

+ Đồ thị hàm số có điểm cực trị là gốc tọa độ, ta có:

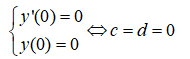
+ Đồ thị hàm số có điểm cực trị là A(-1;-1), ta có:

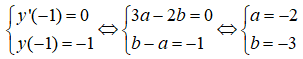
Vậy hàm số là: $y' = - 2 x^{3} - 3 x^{2}$

Câu 18:

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y = \frac{1}{3} x^{3} - \frac{1}{2} m x^{2} + 2 m x - 3 m + 4$ nghịch biến trên một đoạn có độ dài là 3?

A. m = -1; m = 9.

B. m = -1

C. m = 9

D. m = 1; m = -9

Xem đáp án

Chọn A.

Tập xác định: D = R. Ta có

Ta không xét trường hợp y' ≤ 0, ∀ x ∈ R vì a = 1> 0.

Hàm số nghịch biến trên một đoạn có độ dài là 3 ⇔ y' = 0 có 2 nghiệm x1; x2 thỏa mãn:

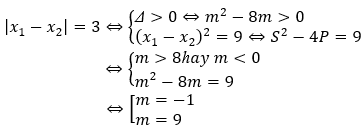
Câu 19:

Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là $f (t) = 45 t^{2} - t^{3}, t = 0, 1, 2, . . ., 25$ . Nếu coi f(t) là hàm số xác định trên đoạn [0;25] thì đạo hàm f’(t) được xem là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Xác định ngày mà tốc độ truyền bệnh là lớn nhất?

A. Ngày thứ 19.

B. Ngày thứ 5.

C. Ngày thứ 16.

D. Ngày thứ 15.

Xem đáp án

Chọn D.

Bảng biến thiên

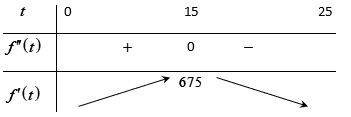
Tốc độ truyền bệnh lớn nhất là vào ngày thứ 15.

Câu 20:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = x^{3} - 3 m x^{2} + 3 m^{3}$ có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 48.

A. m = 2 hoặc m = 0.

B. m = 2

C. m = -2

D. m = ±2

Xem đáp án

Chọn D

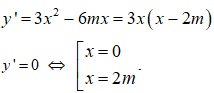
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi : 2m ≠ 0 ⇔ m ≠ 0 (1)

Khi đó, các điểm cực trị của đồ thị hàm số là

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 8 Đề kiểm tra Toán 12 Chương 1 Giải tích có đáp án

Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 4)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương