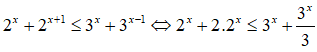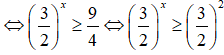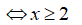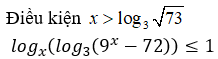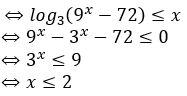Đề kiểm tra 45 phút Toán 12 Chương 1 Giải tích có đáp án (Đề 2)
-
1967 lượt thi
-
25 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số . Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Chọn A.
TXĐ: D = R.
Ta có: ![]()
Do đó, hàm số luôn nghịch biến trên R.
Câu 4:
Đồ thị hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
 Xem đáp án
Xem đáp án
Chọn A
![]()
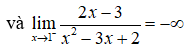 nên đồ thị hàm số có tiệm cận đứng là x = 1 .
nên đồ thị hàm số có tiệm cận đứng là x = 1 .
Tính tương tự với x = 2.
![]() nên đồ thị hàm số có tiệm cận ngang là y = 0.
nên đồ thị hàm số có tiệm cận ngang là y = 0.
Câu 5:
Hàm số có đồ thị là hình vẽ nào sau đây? Hãy chọn câu trả lời đúng.
 Xem đáp án
Xem đáp án
Chọn A.
Hàm số có tiệm cận đứng x = -2.
Tiệm cận ngang y = 2 nên loại đáp án B, D.
Đồ thị hàm số đi qua điểm (- 3; 4) nên chọn đáp án A.
Câu 6:
Cho hàm số Phương trình tiếp tuyến của (C) biết hệ số góc của tiếp tuyến đó bằng 9 là:
 Xem đáp án
Xem đáp án
Chọn A
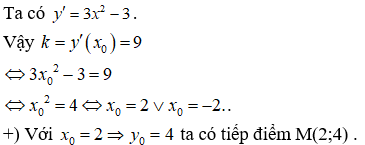
Phương trình tiếp tuyến tại M là
![]()
![]()
![]()
Phương trình tiếp tuyến tại N
![]()
Vậy có hai tiếp tuyến cần tìm là
![]()
Câu 7:
Đồ thị của hàm số( m là tham số) luôn đi qua một điểm M cố định có tọa độ là:
 Xem đáp án
Xem đáp án
Chọn B.
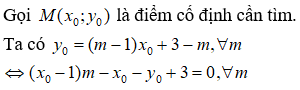
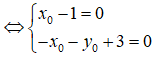
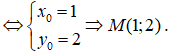
Câu 8:
Cho hàm số . Các đồ thị nào dưới đây có thể là đồ thị biểu diễn hàm số đã cho?
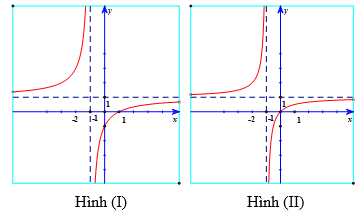
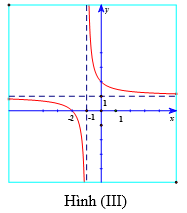
 Xem đáp án
Xem đáp án
Chọn B.
![]()
![]()
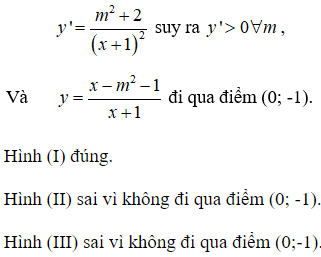
Câu 9:
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?
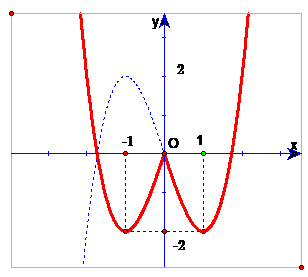
 Xem đáp án
Xem đáp án
Chọn A.
Vì đồ thị đối xứng nhau trục tung và đi qua điểm (-1;-2) và (1;-2).
Câu 10:
Cho đồ thị hàm số và đường thẳng Tìm số giao điểm của đồ thị hàm số (C) và đường thẳng d?
 Xem đáp án
Xem đáp án
Chọn A.
Phương trình hoành độ giao điểm:
![]()
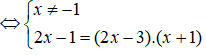
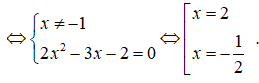
Vậy số giao điểm là 2.
Câu 11:
Cho hàm số . Phương trình tiếp tuyến của (C) tại điểm M có hoành độ biết là
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
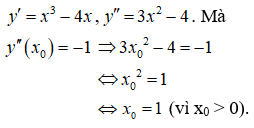
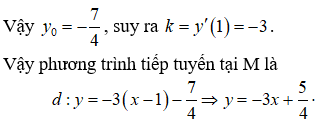
Câu 12:
Đường thẳng y = m không cắt đồ thị hàm số thì tất cả các giá trị tham số m là
 Xem đáp án
Xem đáp án
Chọn A.
Phương trình hoành độ giao điểm:
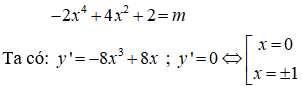
Bảng biến thiên:
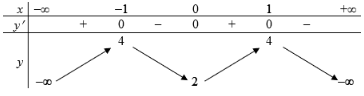
Do đó, đường thẳng y = m không cắt đồ thị hàm số khi m > 4.
Vậy chọn m > 4.
Câu 13:
Cho đồ thị và đường thẳng Tất cả giá trị tham số m để (C) cắt d tại một điểm là
 Xem đáp án
Xem đáp án
Chọn D.
Phương trình hoành độ giao điểm (C) và d là :
![]()
![]()
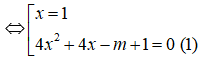
Để (C) cắt d tại một điểm ⇔ Phương trình (1) vô nghiệm hay phương trình (1) có nghiệm kép bằng 1
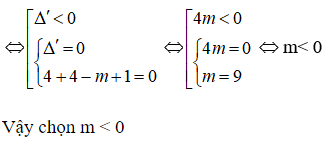
Câu 14:
Với giá trị nào của m thì đồ thị có tiệm cận đứng đi qua điểm ?
 Xem đáp án
Xem đáp án
Chọn D
Để đồ thị hàm số có đường tiệm cận đứng thì luôn đúng với mọi m.
Khi đó đồ thị hàm số có đường tiệm cận đứng là
Vậy để tiệm cận đứng đi qua điểm
![]()
Câu 15:
Đồ thị hàm số có đường tiệm cận đứng khi
 Xem đáp án
Xem đáp án
![]()
Nếu phương trình không có nghiệm x = 1 thì đồ thị hàm số có đường tiệm cận đứng là x = 1.
Nếu phương trình có nghiệm x = 1 hay m = -1.
Khi đó xét giới hạn:
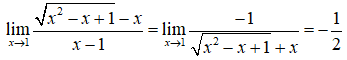
nên trong trường hợp này đồ thị hàm số không có đường tiệm cận đứng.
Vậy m ≠ -1.
Chọn C
Câu 16:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số luôn nghịch biến trên R?
 Xem đáp án
Xem đáp án
Chọn A
Tập xác định: D = R.
![]()
Để hàm số nghịch biến trên R thì
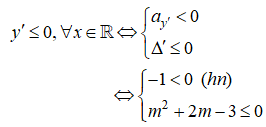
![]()
Câu 17:
Tìm các giá trị của tham số m để hàm số chỉ có đúng một cực trị.
 Xem đáp án
Xem đáp án
Chọn C
+) Trường hợp 1: m = 0
Ta có hàm số: y = -x2, hàm số này có 1 cực trị.
Vậy m = 0 thỏa mãn.
+) Trường hợp 2: m ≠ 0
![]()
![]()
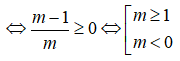
![]()
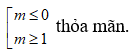
Câu 18:
Một chất điểm chuyển động theo quy luậtvận tốc v (m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm t (s) bằng
 Xem đáp án
Xem đáp án
Chọn A.
Vận tốc của chuyển động là v = s' tức là ![]()
![]()
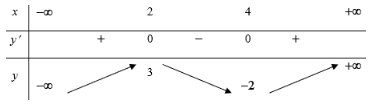
Bảng biến thiên:
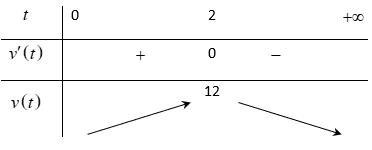
Hàm số v(t) đồng biến trên khoảng (0;2) và nghịch biến trên khoảng (2;+∞)
⇔ Max v(t) = 12 khi t = 2.
Vận tốc đạt giá trị lớn nhất bằng 12 khi t = 2(s).
Câu 19:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số giảm trên nửa khoảng
 Xem đáp án
Xem đáp án
Chọn B.
Tập xác định D = R, yêu cầu của bài toán đưa đến giải bất phương trình
![]()
Tương đương với
![]()
Dễ dàng có được g(x) là hàm tăng ![]()
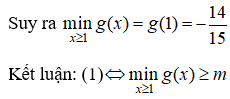
![]()
Câu 20:
Cho hàm số . Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số có ba điểm cực trị tạo thành 1 tam giác nhận gốc tọa độ O làm trực tâm .
 Xem đáp án
Xem đáp án
Chọn D
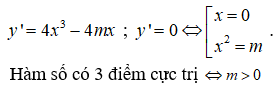
Khi đó đồ thị hàm số có 3 điểm cực trị là:
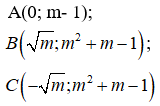
Vì B, C đối xứng với nhau qua trục tung nên
Do đó O là trực tâm tam giác:
![]()
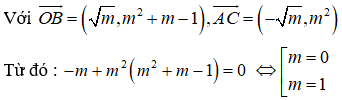
Kết hợp điều kiện, vậy m = 1 là giá trị cần tìm
Câu 21:
Tổng các nghiệm của phương trình
 Xem đáp án
Xem đáp án
Tập xác định: D = R.
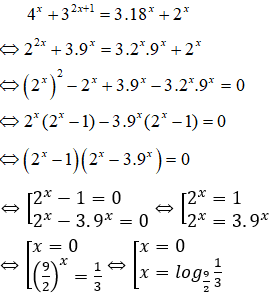
=> tổng hai nghiệm của phương trình là:
Chọn B
Câu 22:
Phương trình có nghiệm là
 Xem đáp án
Xem đáp án
Do hai vế của phương trình đều dương nên lấy logarit cơ số 3 hai vế ta được :
![]()
![]()
![]()
![]()
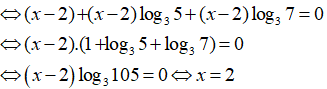
Chọn D
Câu 25:
Tập nghiệm của bất phương trình là:
 Xem đáp án
Xem đáp án

Vậy tập nghiệm của bất phương trình đã cho là
Chọn B