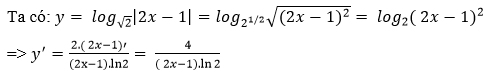25 câu hỏi trắc nghiệm thuộc 200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao (P3)

Câu 1:

Cho hàm số y = log₂( 4^x- 2^x+ m) có tập xác định D = R khi:

A. $m \geq \frac{1}{4}$

B. m > 1/4

C. m < -1/4

D. m > 0

Xem đáp án

Chọn B.

Hàm số có tập xác định là D = R khi và chỉ khi 4^x- 2^x+ m > 0 mọi x. (*)

Đặt t = 2^x> 0 khi đó (*) trở thành : t²– t + m > 0 mọi t > 0.

Hay m > t - t² mọi t > 0

Ta có suy ra

Câu 2:

$y = \log_{2} (\frac{4^{x} + 2^{x + 1} + 10}{2^{x} + 1} - m)$ có tập xác định D = R khi đó có bao nhiêu giá trị nguyên dương của tham số m ?

A. 1

B. 5

C. 10

D. 13

Xem đáp án

Chọn B.

có tập xác định D = R

Ta có

Suy ra m < 6. Vậy có 5 giá trị nguyên dương của m.

Câu 3:

Cho hàm số $y = \sqrt[3]{\ln^{2} (x^{2} + 1) + 2}$ . Mệnh đề nào dưới đây là đúng?

A. $y' = \frac{4 \ln (x^{2} + 1)}{3 y^{2} (x^{2} + 1)}$

B. $y' = \frac{2 x \ln (x^{2} + 1)}{3 y^{2} (x^{2} + 1)}$

C. $y' = \frac{4 x \ln (x^{2} + 1)}{3 y^{2} (x^{2} + 1)}$

D. $y' = \frac{2 \ln (x^{2} + 1)}{3 y^{2} (x^{2} + 1)}$

Xem đáp án

Chọn C.

Ta có

Câu 4:

Cho x; y là các số thực dương thỏa $\log_{9} x = \log_{6} y = \log_{4} (\frac{x + y}{6})$ . Tính tỉ số x/y

A. x/y = 4

B. x/y = 3

C. x/y = 5

D. x/y = 2

Xem đáp án

Chọn D.

Ta có

Từ (1) và (2) ta có

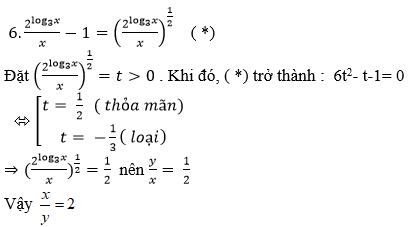
Câu 5:

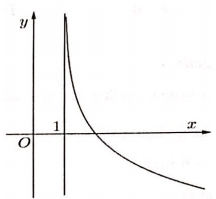
Đồ thị hàm số trong hình bên là đồ thị hàm số nào trong các hàm số dưới đây.

A. y = ln( x - 1)

B. $y = \log_{\frac{1}{2}} (x - 1)$

C. y = 2^x-1

D. $y = {(\frac{1}{2})}^{x - 1}$

Xem đáp án

Chọn B.

Nhận xét hàm số đã cho là hàm nghịch biến( loại A và C).

Mặt khác đồ thị hàm số đã cho nhận x = 1 là đường tiệm cận đứng

(Đáp án D là có tiệm cận ngang; không có tiệm cận đứng)

Câu 6:

Cho hàm số sau: y = f(x) = ( x²- 2( m + 4) x + 2m + 12).e^x. Tìm tổng các giá trị nguyên của m để hàm số nghịch biến trên TXĐ là S thì giá trị của S sẽ là:

A. 15

B. -12

C. -15

D. -10

Xem đáp án

Chọn C.

+) TXĐ: D = R

+) y = f(x) = ( x²- 2( m + 4) x + 2m + 12).e^x

$\Rightarrow y' = [2 x - 2 (m + 4)] e^{x} + [x^{2} - 2 (m + 4) x + 2 m + 12] e^{x} = [x^{2} - 2 (m + 3) x + 4] e^{x}$

Hàm số nghịch biến trên TXĐ khi y’ = ( x²- 2( m + 3) x + 4) .e^x ≤ 0 mọi x

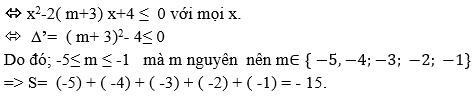
Câu 7:

Cho $α, β$ là các số thực. Đồ thị các hàm số $y = x^{α}, y = x^{β}$ trên khoảng $(0; + \infty)$ được cho hình vẽ bên. Khẳng định nào sau đây đúng?

A. $0 < β < 1 < α$

B. $β < 0 < 1 < α$

C. $0 < α < 1 < β$

D. $α < 0 < 1 < β$

Xem đáp án

Chọn D.

Với x₀> 1 ta có:

Mặt khác, dựa vào hình dáng đồ thị ta suy ra và

Câu 8:

Trong hình vẽ bên đồ thị (1) là của hàm số y = log_ax và đồ thị (2) là của hàm số y = log_bx. Khẳng định nào sau đây là đúng.

A. a > b > 1

B. b > a > 1

C. 1 > a > b > 0

D. 1 > b > a > 0

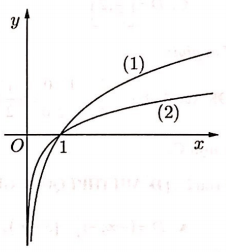
Xem đáp án

Chọn B.

Dựa vào đồ thị ta thấy 2 hàm số đã cho phải là 2 hàm đồng biến như vậy a; b > 1

Mặt khác chọn x = 2 ta có:

Do đó b > a > 1.

Câu 9:

Hỏi có bao nhiêu giá trị nguyên của m để phương trình 3^x+m²=10m-9 có nghiệm thực?

A. 7

B. 9

C. 6

D. 10

Xem đáp án

Chọn A.

Phương trình đã cho tương đương 3^x= -m²+10m-9 (1)

Phương trình (1) có nghiệm thực khi và chỉ khi -m²+10m -9>0 hay 1<m<9

Mà

Câu 10:

Cho hàm số $y = \frac{m \ln x + 1}{\ln x - m}$ có giá trị nhỏ nhất trên [1; e] bằng -3. Chọn khẳng định đúng về tham số m?

A. m > 2

B. m > 5

C. m < 3

D. m < 0

Xem đáp án

Chọn C.

Với 1 ≤ x ≤ e, ta có:

Điều kiện:

suy ra ( thỏa điều kiện).

Câu 11:

Tìm tất cả các giá trị của tham số m sao cho hàm số $y = \frac{e^{x} - m - 2}{e^{x} - m^{2}}$ đồng biến trên khoảng $(\ln \frac{1}{4}; 0)$

A. 1 < m < 2

B. $m \in [- \frac{1}{2}; \frac{1}{2}]$

C. $m \in [- \frac{1}{2}; \frac{1}{2}] \cup (1; 2) \ \{0\}$

D. 1 ≤ m ≤ 2

Xem đáp án

Chọn C.

+ Khi m = 0 thì có . Thỏa yêu cầu bài toán.

+ Khi m ≠ 0 ta có ĐK là e^x ≠ m² hay x ≠ ln m² , ta có

Yêu cầu bài toán tương đương

$\{\begin{cases} - m^{2} + m + 2 > 0 \\ [\begin{matrix} \ln m^{2} \leq \ln \frac{1}{4} \\ \ln m^{2} \geq 0 \end{matrix} \end{cases} \Leftrightarrow \{\begin{cases} - 1 < m < 2 \\ [\begin{matrix} m^{2} \leq \frac{1}{4} \\ m^{2} \geq 1 \end{matrix} \end{cases} \Leftrightarrow \{\begin{array}{l} - 1 < m < 2 \\ [\begin{matrix} m \in [- \frac{1}{2}; \frac{1}{2}] \\ m \in (- \infty; - 1] \cup [1; + \infty) \end{matrix} \end{array} \Leftrightarrow m \in [- \frac{1}{2}; \frac{1}{2}] \cup [1; 2) \ \{0\}$

Câu 12:

Cho hai số thực dương a ; b khác 1 Biết rằng bất kì đường thẳng nào song song với trục hoành mà cắt các đường y = a^x; y =b^x và trục tung lần lượt tại M ; N ; A thì AN = 3AM ( hình vẽ bên ).

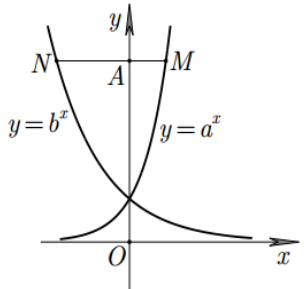
Hỏi khẳng định nào sau đây đúng ?

A. ab²= 1

B. b = 3a

C. a³b = 1

D. ab³= 1

Xem đáp án

Chọn D.

Câu 13:

Tập xác định của hàm số $y = \sqrt{\ln (e x^{2}) - 2}$ là:

A. $D = (\sqrt{e}; + \infty)$

B. $D = (0; + \infty)$

C. $D = (\frac{e}{2}; + \infty)$

D. $D = (- \infty; - \sqrt{e}) \cup (\sqrt{e}; + \infty)$

Xem đáp án

Chọn D.

$y = \sqrt{\ln (e x^{2}) - 2}$

Hàm số đã cho xác định khi

$\{\begin{cases} e x^{2} > 0 \\ \ln (e x^{2}) - 2 \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq 0 \\ x^{2} \geq e \end{cases} \Leftrightarrow \{\begin{cases} x \neq 0 \\ [\begin{matrix} x < - \sqrt{e} \\ x > \sqrt{e} \end{matrix} \end{cases}$

Do đó tập xác định: $D = (- \infty; - \sqrt{e}) \cup (\sqrt{e}; + \infty)$

Câu 14:

Tập xác định của hàm số y = log₂( log₃x - 1) là:

A. $D = (0; + \infty)$

B. $D = (3; + \infty)$

C. $D = (1; + \infty)$

D. $D = (\frac{1}{3}; + \infty)$

Xem đáp án

Chọn B.

Hàm số đã cho xác định khi $\{\begin{cases} x > 0 \\ \log_{3} x - 1 > 0 \end{cases} \Leftrightarrow \{\begin{cases} x > 0 \\ \log_{3} x > 1 \end{cases} \Leftrightarrow \{\begin{cases} x > 0 \\ x > 3 \end{cases} \Leftrightarrow x > 3$

Khi đó tập xác định của hàm số là $(3; + \infty)$

Câu 15:

Đạo hàm của hàm số $y = e^{\sqrt{x}} - e^{- \sqrt{x}}$ là:

A. $y' = \frac{e^{\sqrt{x}} + e^{- \sqrt{x}}}{2 \sqrt{x}}$

B. $y' = \frac{e^{\sqrt{x}} - e^{- \sqrt{x}}}{2 \sqrt{x}}$

C. $y' = \frac{e^{\sqrt{x}} - e^{- \sqrt{x}}}{\sqrt{x}}$

D. $y' = \frac{e^{\sqrt{x}} + e^{- \sqrt{x}}}{\sqrt{x}}$

Xem đáp án

Chọn A.

Ta có:

Câu 16:

Đạo hàm của hàm số $y = \log_{\frac{3}{2}} |x|$ là:

A. $y' = \frac{- 1}{x (\ln 3 - \ln 2)}$

B. $y' = \frac{1}{|x| (\ln 3 - \ln 2)}$

C. $y' = \frac{1}{x (\ln 3 - \ln 2)}$

D. $y' = \frac{3}{2 x (\ln 3 - \ln 2)}$

Xem đáp án

Chọn C.

Câu 17:

Đạo hàm của hàm số $y = \log_{\sqrt{2}} |2 x - 1|$ là:

A. $y' = \frac{1}{(2 x - 1) \ln 2}$

B. $y' = \frac{4}{(2 x - 1) \ln 2}$

C. $y' = \frac{2}{(2 x - 1) \ln 2}$

D. $y' = \frac{1}{|2 x - 1| \ln 2}$

Xem đáp án

Chọn B.

Câu 18:

Đạo hàm của hàm số $y = \frac{\sin (x^{2} + 1)}{2^{x}}$ là:

A. $\frac{\cos (x^{2} + 1) - \ln 2 . \sin (x^{2} + 1)}{2^{x}}$

B. $\frac{\cos (x^{2} + 1) - \ln 2 . \sin (x^{2} + 1)}{4^{x}}$

C. $\frac{2 x \cos (x^{2} + 1) - \ln 2 . \sin (x^{2} + 1)}{2^{x}}$

D. $\frac{- 2 x \cos (x^{2} + 1) - \ln 2 . \sin (x^{2} + 1)}{2^{x}}$

Xem đáp án

Chọn C.

Ta có:

Câu 19:

Đạo hàm của hàm số $y = \ln |x - 2| + 2^{x}$ là:

A. $y' = \frac{1}{|x - 2|} + 2^{x} \ln 2$

B. $y' = \frac{1}{|x - 2|} + 2^{x}$

C. $y' = \frac{1}{x - 2} + 2^{x} \ln 2$

D. $y' = \frac{1}{x - 2} + 2^{x}$

Xem đáp án

Chọn C.

Ta có:

Do đó

Câu 20:

Đạo hàm của hàm số $y = \ln \sqrt{x^{2} + 2 x + 3}$ là:

A. $y' = \frac{x + 1}{2 \sqrt{x^{2} + 2 x + 3}}$

B. $y' = \frac{2 x + 2}{\sqrt{x^{2} + 2 x + 3}}$

C. $y' = \frac{x + 1}{\sqrt{x^{2} + 2 x + 3}}$

D. $y' = \frac{x + 1}{x^{2} + 2 x + 3}$

Xem đáp án

Chọn D.

Ta có:

Do đó:

Câu 21:

Đạo hàm của hàm số $y = \ln \sqrt{\frac{x + 1}{x - 1}}$ là:

A. $y' = \frac{- 1}{x^{2} - 1}$

B. $y' = \frac{1}{x^{2} - 1}$

C. $y' = \frac{1}{2 (x^{2} - 1)}$

D. $y' = \frac{- 1}{2 (x^{2} - 1)}$

Xem đáp án

Chọn A.

Ta có:

Do đó:

Câu 22:

Đạo hàm của hàm số $f (x) = \ln (x + \sqrt{1 + x^{2}})$ là:

A. $f' (x) = \frac{1}{\sqrt{x^{2} + 1}}$

B. $f' (x) = \frac{1}{x + \sqrt{x^{2} + 1}}$

C. $f' (x) = \frac{1}{x + \sqrt{x^{2} + 1}} (1 + \frac{1}{2 \sqrt{x^{2} + 1}})$

D. $f' (x) = \frac{2 x}{\sqrt{x^{2} + 1}}$

Xem đáp án

Chọn A.

Ta có:

Câu 23:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = 2^{\sin^{2} x} + 2^{\cos^{2} x}$ là:

A. $\underset{ℝ}{m i n} y = 2 \sqrt{2}; \underset{ℝ}{m a x} y = 3$

B. $\underset{ℝ}{m i n} y = 2; \underset{ℝ}{m a x} y = 3$

C. $\underset{ℝ}{m i n} y = 3; \underset{ℝ}{m a x} y = 3 \sqrt{2}$

D. $\underset{ℝ}{m i n} y = 2; \underset{ℝ}{m a x} y = 3 \sqrt{2}$

Xem đáp án

Chọn A.

Ta có: . Đặt , do 0 ≤ cos²x ≤ 1 nên ta có

Xét hàm số có

Lại có

Vậy

Câu 24:

Giá trị lớn nhất và nhỏ nhất của hàm số y = 4^x- 2^x+1 trên đoạn [- 1;1]

A. $\underset{[- 1; 1]}{m i n} y = - \frac{3}{4}; \underset{[- 1; 1]}{m a x} y = 2$

B. $\underset{[- 1; 1]}{m i n} y = - \frac{3}{4}; \underset{[- 1; 1]}{m a x} y = 0$

C. $\underset{[- 1; 1]}{m i n} y = - 1; \underset{[- 1; 1]}{m a x} y = 1$

D. $\underset{[- 1; 1]}{m i n} y = - 1; \underset{[- 1; 1]}{m a x} y = 0$

Xem đáp án

Chọn B.

Ta có: y = 2^2x- 2.2^x . Đặt

Xét hàm số f(t) = t²- 2t trên đoạn ta có: f’(t) = 2t - 2 và f’(t) = 0 khi t = 1

Hàm số f(t) xác định và liên tục trên đoạn

Lại có f(0,5) = -3/4; f(1) = -1; f(2) = 0 . Do đó $\underset{[- 1; 1]}{m i n} y = - \frac{3}{4}; \underset{[- 1; 1]}{m a x y} = 0$

Câu 25:

Giá trị lớn nhất và nhỏ nhất của hàm số $y = 5^{\sqrt{x}} + 5^{1 - \sqrt{x}}$ trên đoạn [0;1] là:

A. $\underset{[0; 1]}{m i n} y = 2 \sqrt{5}; \underset{[0; 1]}{m a x} y = 6$

B. $\underset{[0; 1]}{m i n} y = 2 \sqrt{5}; \underset{[0; 1]}{m a x} y = 5$

C. $\underset{[0; 1]}{m i n} y = 2; \underset{[0; 1]}{m a x} y = 6$

D. $\underset{[0; 1]}{m i n} y = 2; \underset{[0; 1]}{m a x} y = 5$

Xem đáp án

Chọn A.

Ta có: . Đặt

Khi đó

Hàm số f(t) xác định và liên tục trên đoạn [1 ;5]

Ta có: . Do đó .

CHỌN BỘ SÁCH BẠN MUỐN XEM

200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao

200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao (P3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương