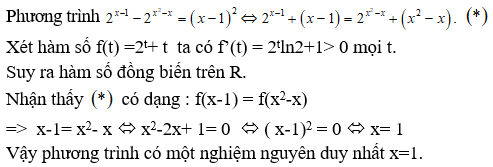25 câu hỏi trắc nghiệm thuộc 200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao (P5) - hamchoi.vn

200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao

200 câu trắc nghiệm Hàm số mũ và Logarit nâng cao (P5)

1259 lượt thi
25 câu hỏi
25 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Biết rằng phương trình $9^{x^{2} - 2 x} . 7^{x} = \frac{7}{9}$ . Có hai nghiệm phân biệt là x₁; x₂. Tổng x₁+x₂ có dạng $\log_{9} \frac{a}{b}$ với a ; b nguyên dương và $\frac{a}{b}$ là phân số tối giản. Tính S = a + 2b

A. 95

B. 100

C. 36

D. 32

Chọn A.

Phương trình:

Câu 2:

Biết rằng phương trình $2^{x} . 3^{\frac{2 x + 1}{x + 2}} = 6$ có hai nghiệm phân biệt là x₁; x₂. Tính giá trị của biểu thức S = x₁+ x₂

A. $S = \log_{2} \frac{3}{2}$

B. $S = \log_{2} \frac{2}{3}$

C. $S = \log_{3} \frac{3}{2}$

D. $S = \log_{3} \frac{2}{3}$

Chọn A.

Điều kiện:

Phương trình

Do đó S = -1 + log₂3 = log₂3 – log₂2 = log₂3/2.

Câu 3:

Phương trình ${(x + 2)}^{x^{2} - 5 x + 6} = 1$ có số nghiệm là?

A. 4

B. 2

C. 3

D. 1

Chọn A.

+TH1:

Thử lại ta thấy thỏa mãn phương trình đã cho.

+TH2. x + 2 = 1 hay x = -1 , thử lại ta thấy thỏa mãn phương trình đã cho

+TH3. x + 2 = -1 hay x = -3 , thử lại ta thấy thỏa mãn phương trình đã cho

Vậy phương trình đã cho có nghiệm là x = - 1; x = 2; x = -3; x = 3.

Câu 4:

Phương trình ${(x^{2} + x - 3)}^{x^{2} - 2 x + 3} = {(x^{2} + x - 3)}^{x + 1}$ có số nghiệm là?

A. 6

B. 5

C. 3

D. 4

Chọn B.

Câu 5:

Giải phương trình ${(7 + 4 \sqrt{3})}^{x} - 4 {(2 + \sqrt{3})}^{x} + 4 = 0$

A. $x = - \log_{2 + \sqrt{3}} 2$

B. $x = \log_{2 + \sqrt{3}} 2$

C. $x = - \log_{2 + \sqrt{3}} 4$

D. $x = \log_{2 + \sqrt{3}} 4$

Chọn B.

Phương trình

Câu 6:

Biết rằng phương trình 2^3x- 3.2^2x+1+ 11.2^x– 6 = 0 có ba nghiệm phân biệt $x_{1}, x_{2}, x_{3}$ .Tính S = x₁+ x₂+ x₃

A. log₂24

B. log₂12

C. log₂18

D. log₂6

Chọn D.

Phương trình thỏa mãn (*)

Do đó S = 1+ log₂3 = log₂6.

Câu 7:

Biết rằng 8^x- 6.12^x+11.8^x- 6.27^x= 0 có ba nghiệm phân biệt. Tính $S = \frac{2}{x_{1} + x_{2} + x_{3}}$

A. 2 - 4log₆2

B. 2 -log₆3

C. 2 - 4log₆3

D. 2 + 4log₆3

Chọn C.

Phương trình <=>

Câu 8:

Phương trình $1 + 2^{8 - 5 x} = 2^{x^{2} - 5 x + 5} + 2^{3 - x^{2}}$ có số nghiệm là?

A. 4

B. 2

C. 3

D. 1

Chọn A.

Câu 9:

Biết rằng phương trình ${(3 + \sqrt{5})}^{2} + 3 {(3 - \sqrt{5})}^{2} = 2^{x + 2}$ có hai nghiệm phân biệt là $x_{1} > x_{2}$ . Nghiệm $x_{1}$ có dạng $\log_{\frac{a + b \sqrt{5}}{2}} 9$ , với a; b nguyên dương. Tính S = a⁴+ 10ab

A. 2611

B. 2681

C. 2422

D. 2429

Chọn A.

Ta có

Phương trình đã cho thành

đây là phương trình đẳng cấp, ta có thể chia cả hai vế cho b > 0 như sau:

$\frac{a}{b} + 3 = 4 \sqrt{\frac{a}{b}} \Leftrightarrow \frac{a}{b} - 4 \sqrt{\frac{a}{b}} + 3 = 0 \Leftrightarrow [\begin{matrix} \sqrt{\frac{a}{b}} = 1 \\ \sqrt{\frac{a}{b}} = 3 \end{matrix} \Leftrightarrow [\begin{matrix} \frac{a}{b} = 1 \\ \frac{a}{b} = 9 \end{matrix}$

+) TH1. $\frac{a}{b} = 1$

$\Rightarrow \frac{{(3 + \sqrt{5})}^{x}}{{(3 - \sqrt{5})}^{x}} = 1 \Leftrightarrow {(\frac{3 + \sqrt{5}}{3 - \sqrt{5}})}^{x} = 1 \Leftrightarrow x = 0$

+) TH2. $\frac{a}{b} = 9$

$\Rightarrow \frac{{(3 + \sqrt{5})}^{x}}{{(3 - \sqrt{5})}^{x}} = 9 \Leftrightarrow {(\frac{3 + \sqrt{5}}{3 - \sqrt{5}})}^{x} = 9 \Leftrightarrow {(\frac{7 + 3 \sqrt{5}}{2})}^{x} = 9 \Leftrightarrow x = \log_{\frac{7 + 3 \sqrt{5}}{2}} 9$

Do đó

Câu 10:

Biết rằng phương trình $5^{3 x} + 9 . 5^{x} + \frac{27}{125^{x}} + \frac{27}{5^{x}} = 64$ có hai nghiệm phân biệt là x₁< x₂. Tính S = x₁+ 2x₂

A. log₅18

B. log₅9

C. log₅3

D. log₅15

Chọn B.

Phương trình

thỏa mãn (*)

Do đó

Câu 11:

Phương trình 2^x= 3 - x có số nghiệm là ?

A. 2

B. 3

C. 1

D. 4

Chọn C.

Phương trình tương đương: 2^x+ x – 3 = 0 (1)

Xét hàm số f(x) = 2^x+ x - 3 với có f’(x) = 2^xln2 + 1 > 0

Suy ra hàm số đồng biến trên R.

Do đó trên R phương trình f(x) = 0 nếu có nghiệm thì sẽ có nghiệm duy nhất.

Mà f(1) = 0 nên x = 1 là nghiệm duy nhất của (1).

Câu 12:

Tìm số nghiệm của phương trình $2^{\frac{1}{x}} + 2^{\sqrt{x}} = 3$

A. Có nghiệm.

B. Có vô số nghiệm.

C. Có nghiệm.

D. Không có nghiệm.

Chọn D.

Đk: x > 0

Xét (2)

Xét (3)

Từ (1); (2) ; (3) suy ra phương trình đã cho không có nghiệm.

Câu 13:

Cho phương trình $2016^{x^{2} - 1} + (x^{2} - 1) . 2017^{x} = 1 (1)$ Khẳng định nào dưới đây đúng?

A. Phương trình (1) có nghiệm duy nhất.

B. Phương trình (1) vô nghiệm.

C. Phương trình (1) có tổng các nghiệm bằng 0.

D. Phương trình (1) có nhiều hơn hai nghiệm.

Chọn C.

=>Phương trình đã cho có 2 nghiệm và tổng hai nghiệm là 0

Câu 14:

Phương trình ${(\sqrt{3} - \sqrt{2})}^{x} + {(\sqrt{3} + \sqrt{2})}^{x} = {(\sqrt{10})}^{x}$ có tất cả bao nhiêu nghiệm thực.

A. 1.

B. 2.

C. 3.

D. 4.

Chọn A.

Câu 15:

Phương trình 3^2x+ 2x( 3^x+ 1) – 4.3^x– 5 = 0 có tất cả bao nhiêu nghiệm không âm?

A. 1.

B. 2.

C. 0.

D. 3.

Chọn A.

Ta có:

$3^{2 x} + 2 x (3^{x} + 1) - 4 . 3^{x} - 5 = 0 \Leftrightarrow (3^{2 x} - 1) + 2 x (3^{x} + 1) - 4 . 3^{x} - 4 = 0 \Leftrightarrow (3^{x} + 1) (3^{x} - 1) + 2 x (3^{x} + 1) - 4 (3^{x} + 1) = 0 \Leftrightarrow (3^{x} + 1) (3^{x} - 1 + 2 x - 4) = 0 \Leftrightarrow (3^{x} + 1) (3^{x} + 2 x - 5) = 0$

$\Leftrightarrow [\begin{matrix} 3^{x} + 1 = 0 \\ 3^{x} + 2 x - 5 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} 3^{x} + 1 = 0 \\ 3^{x} + 2 x - 5 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} 3^{x} + 1 = 0 (v ô l ý) \\ 3^{x} + 2 x - 5 = 0 \end{matrix}$

Xét hàm số: $f (x) = 3^{x} + 2 x - 5$

$\Rightarrow f' (x) = 3^{x} \ln 3 + 2 > 0$

Do đó hàm số đồng biến trên R

Suy ra phương trình f(x) = 0 có tối đa 1 nghiệm

Lại có f(1) = 0 nên nghiệm duy nhất của phương trình là x = 1.

Câu 16:

Phương trình $2^{x - 1} - 2^{x^{2} - x} = {(x - 1)}^{2}$ có tất cả bao nhiêu nghiệm?

A. 1.

B. 2.

C. 3.

D. 4.

Chọn A.

Câu 17:

Tính tổng T tất cả các nghiệm của phương trình $2017^{\sin^{2} x} - 2017^{\cos^{2} x} = \cos 2 x$ trên đoạn $[0; π]$

A. $x = π$

B. $x = \frac{π}{4}$

C. $x = \frac{π}{2}$

D. $x = \frac{3 π}{4}$

Chọn A.

Phương trình

Xét hàm số f(t) = 2017^t + t ; ta có f’(t) = 2017^tln2017 + 1 > 0 mọi x

Suy ra hàm số đồng biến trên R.

Nhận thấy (*) có dạng f( sin²x) = f(cos²x) ; do đó: sin²x = cos²x

Vì

Câu 18:

Biết rằng phương trình $3^{x^{2} - 1} + (x^{2} - 1) 3^{x + 1} = 1$ có đúng hai nghiệm phân biệt. Tổng lập phương hai nghiệm của phương trình bằng:

A. 2.

B. 0.

C. 8.

D. -8.

Chọn B.

+ Nếu thì x²- 1 > 0.

Suy ra . Do đó phương trình đã cho vô nghiệm.

+ Nếu -1 < x < 1 thì x²- 1 < 0. Suy ra Do đó phương trình đã cho vô nghiệm.

+ Kiểm tra x = 1 ; x = -1 thỏa mãn phương trình đã cho. Vậy phương trình đã cho có hai nghiệm x = -1 ; x = 1.

Suy ra .

Câu 19:

Cho phương trình $2016^{x^{2} - 1} + (x^{2} - 1) . 2017^{x} = 1$ . Mệnh đề nào sau đây là đúng?

A. Phương trình đã cho có tổng các nghiệm bằng 0.

B. Phương trình đã cho có nghiệm duy nhất.

C. Phương trình đã cho có hai nghiệm dương phân biệt.

D. Phương trình đã cho có nhiều hơn hai nghiệm.

Chọn A.

+Nếu thì x²– 1 > 0. Suy ra

. Do đó phương trình đã cho vô nghiệm.

+ Nếu -1 < x < 1 thì x²- 1 < 0. Suy ra

. Do đó phương trình đã cho vô nghiệm.

+ Kiểm tra x = 1 ; x = -1 thỏa mãn phương trình đã cho.

Vậy phương trình đã cho có hai nghiệm x = -1 ; x = 1.

Suy ra phương trình đã cho có tổng các nghiệm bằng 0.

Câu 20:

Phương trình 4^x+ 2^x(x - 7) - 4x + 12 = 0 có số nghiệm là?

A. 3

B. 1

C. 2

D. 4

Chọn C.

Đặt t = 2^x> 0 phương trình đã cho thành : t²+ (x - 7) t - 4x + 12 = 0 (1)

Coi (1) là phương trình bậc hai ẩn t, ta có

∆ = (x - 7) ²- 4( -4x + 12) = (x + 1) ²≥ 0

Do đó (1) $\Leftrightarrow [\begin{matrix} t = \frac{7 - x + (x + 1)}{2} = 4 \\ t = \frac{7 - x - (x + 1)}{2} = 3 - x \end{matrix}$

+ TH1. t = 4 thì 2^x= 4 nên x = 2

+ TH2. t = 3 - x thì 2^x= 3 - x

Vì $t > 0 \Rightarrow 3 - x > 0 \Leftrightarrow x < 3$

Xét hàm số: $f (x) = 2^{x} + x - 3$

$\Rightarrow f' (x) = 2^{x} \ln 2 + 1 > 0 \forall x < 3$

Nên hàm số f(x) luôn đồng biến $\forall x < 3$

Do đó phương trình $f (x) = 0$ có một nghiệm duy nhất

Lại có f(1) = 0 nên x = 1 là nghiệm của phương trình $f (x) = 0$

Tóm lại, phương trình đã cho có nghiệm là 1 và 2.

Câu 21:

Phương trình $2^{2 x^{2} - 4 x + 3} - 15 x + 15 = 2^{2 x^{2} + x - 2}$ có số nghiệm nguyên âm là:

A. 1

B. 2

C. 0

D. 3

Chọn C.

Ta biến đổi phương trình

$2^{2 x^{2} - 4 x + 3} + 3 (2 x^{2} - 4 x + 3) = 2^{2 x^{2} + x - 2} + 3 (2 x^{2} + x - 2)$

Xét hàm f(t) = $2^{t} + 3 t$

$\Rightarrow f' (t) = 2^{t} \ln 2 + 3 > 0 \forall t$

Do đó hàm số f(t) đồng biến trên R, khi đó ta có:

$2 x^{2} - 4 x + 3 = 2 x^{2} + x - 2 \Leftrightarrow 5 x = 5 \Leftrightarrow x = 1$

Vậy phương trình đã cho không có nghiệm nguyên âm.

Câu 22:

Tìm tất cả các nghiệm của phương trình $4^{x^{2} - 3 x + 2} + 4^{x^{2} + 6 x + 5} = 4^{2 x^{2} + 3 x + 7} + 1$

A. $x \in \{- 5; - 1; 1; 2\}$

B. $x \in \{- 5; - 1; 1; 3\}$

C. $x \in \{- 5; - 1; 1; - 2\}$

D. $x \in \{5; - 1; 1; 2\}$

Chọn A.

Câu 23:

Phương trình $2^{x^{2} + 1} + 3^{x^{2} + 2} = 5 (\sin x + \cos x)$ có số nghiệm là ?

A. 2

B. 1

C. 0

D. 3

Chọn C.

Ta có

Ta có: $\sin x + \cos x = \sqrt{2} \sin (x + \frac{π}{4})$

$\Rightarrow 5 (\sin x + \cos x) = 5 . \sqrt{2} \sin (x + \frac{π}{4})$

Mà $- 1 \leq \sin (x + \frac{π}{4}) \leq 1$

$\Rightarrow - 5 \sqrt{2} \leq \sin (x + \frac{π}{4}) \leq 5 \sqrt{2}$

phương trình vô nghiệm.

Câu 24:

Phương trình $2^{x} + 3^{x} = \frac{5}{\sqrt{x} + \sqrt{4 - x} + 1}$ có số nghiệm là?

A. 0

B. 1

C. 2

D. 3

Chọn A.

Điều kiện:

Khi đó

phương trình vô nghiệm.

Câu 25:

Phương trình $2^{x} + 2^{- x} = \frac{4}{\sqrt{x} + \sqrt{1 - x} + 1}$ có nghiệm là ?

A. 2

B. 1

C. 0

D. 3

Chọn B.

Điều kiện: (*)

Ta có

Lại có

, dấu xảy ra khi x = 0.

Thử lại, ta thấy x = 0 thỏa mãn phương trình đã cho.

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương