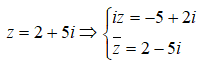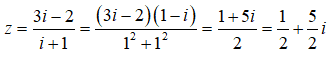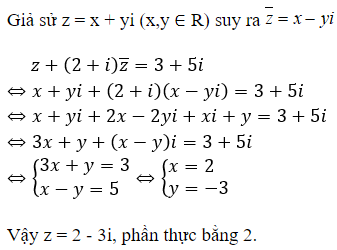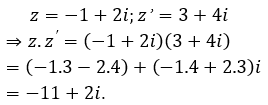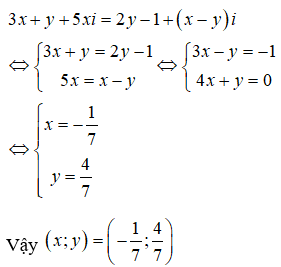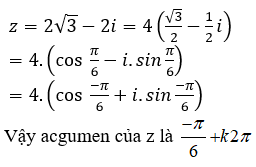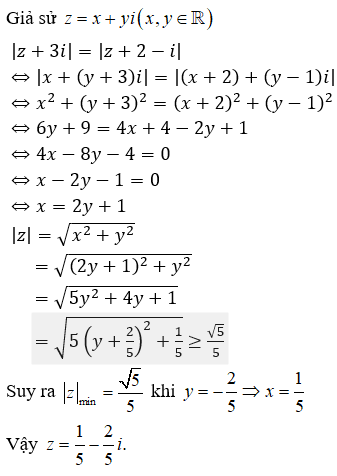Đề kiểm tra 45 phút Toán 12 Chương 4 Giải tích có đáp án (Đề 1)
-
1647 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 4:
Trong C, phương trình có nghiệm là:
 Xem đáp án
Xem đáp án
Chọn A.
Ta có: Δ = b2 - 4ac = 12 - 4.2.1 = -7 = 7i2 < 0 nên phương trình có hai nghiệm phức là:
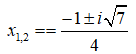
Câu 6:
Biết là hai nghiệm của phương trình Khi đó giá trị của là:
 Xem đáp án
Xem đáp án
Chọn A.
Theo Viet, ta có:
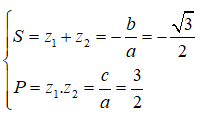
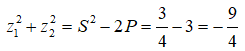
Câu 7:
Điểm M biểu diễn số phức trong mặt phẳng tọa độ phức là:
 Xem đáp án
Xem đáp án
Chọn B.
Số phức z có phần thực là 3, phần ảo là 2 nên điểm biểu diễn trên mặt phẳng tọa độ là điểm M(3; 2)
Câu 11:
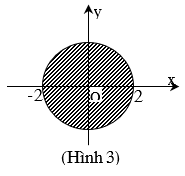
Cho số phức Để điểm biểu diễn của z nằm trong hình tròn như hình 3 (không tính biên), điều kiện của a và b là:
 Xem đáp án
Xem đáp án
Chọn C.
Ta thấy miền mặt phẳng trên hình là hình tròn tâm O(0;0) bán kính bằng R = 2, gọi M(a;b) là điểm thuộc miền mặt phẳng đó thì M(a;b) = {a; b ∈ R; a2 + b2 < 4}
Câu 13:
Giá trị của các số thực b, c để phương trình nhận số phức làm một nghiệm là:
 Xem đáp án
Xem đáp án
Chọn C.
Do z = 1 + i là một nghiệm của z2 + bz + c = 0 nên ta có:
![]()
![]()
![]()

Câu 14:
Tập hợp điểm biểu diễn số phức z thỏa mãn |z| = 1 và phần ảo của z bằng 1 là:
 Xem đáp án
Xem đáp án
Chọn C
Gọi M(a; b) là điểm biểu diễn số phức A(-1,1), R = 1
Ta có:
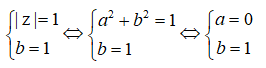
Khi đó, số phức z = i và M(0;1)
Vì a2 + b2 = 1 nên điểm M biểu diễn số phức z thuộc đường tròn tâm O(0;0), bán kính R = 1
Vì điểm M(0; 1) nên M thuộc đường thẳng y = 1.
Tập hợp các điểm biểu diễn là giao điểm của đường tròn tâm O, bán kính R = 1 và đường thẳng y = 1.
Câu 15:
Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện
 Xem đáp án
Xem đáp án
Chọn C
Gọi M(x ; y) là điểm biểu diễn của số phức z = x + yi trong mặt phẳng phức (x, y ∈ R).
Theo đề bài ta có:
![]()
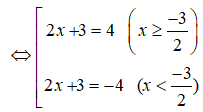
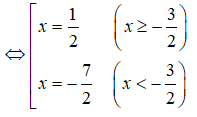
Vậy tập hợp điểm M(x;y) cần tìm là đường thẳng đường thẳng với , và đường thẳng
Câu 18:
Cho số phức z thỏa mãn . Viết z dưới dạngKhi đó tổng a + b có giá trị bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Chọn C
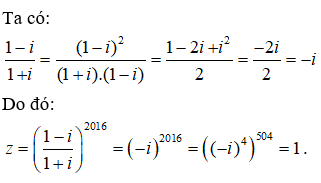
Câu 19:
Cho số phức , m nguyên dương. Có bao nhiêu giá trị m ∈ [1;100] để z là số thực?
 Xem đáp án
Xem đáp án
Chọn C.
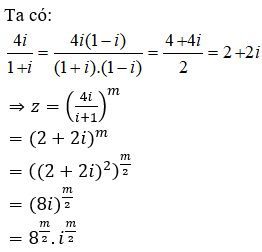
Để z là số thực khi và chỉ khi
![]()
Mà m ∈ [1;100] nên m ∈ {4;8;12;....;96;100}
![]()
giá trị m thỏa yêu cầu đề bài.