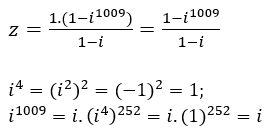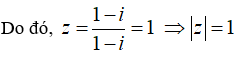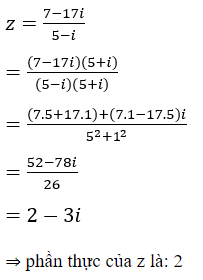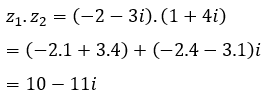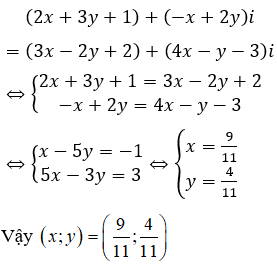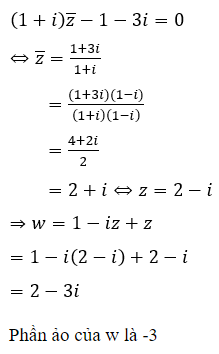20 câu hỏi trắc nghiệm thuộc Đề kiểm tra 45 phút Toán 12 Chương 4 Giải tích có đáp án (Đề 3)

Câu 1:

Cho số phức $z = 6 + 7 i .$ Số phức liên hợp của z là

A. $\bar{z} = 6 + 7 i$

B. $\bar{z} = - 6 - 7 i$

C. $\bar{z} = - 6 + 7 i$

D. $\bar{z} = 6 - 7 i$

Xem đáp án

Chọn D.

Câu 2:

Cho $z_{1} = 2 - 3 i; z_{2} = - 2 + 8 i . T í n h z_{1} + z_{2} ?$

A. 2 + 5i

B. 5i

C. 4 + 5i

D. 4

Xem đáp án

Chọn B.

Ta có: z1 + z2 = (2 - 2) + (-3 + 8)i = 5i

Câu 3:

Số phức $z = \frac{7 - 17 i}{5 - i}$ có phần thực là

A. 2

B. $\frac{9}{13}$

C 3

D. -3

Xem đáp án

Chọn A.

Câu 4:

Cho hai số phức $z_{1} = - 2 - 3 i; z_{2} = 1 + 4 i . T í n h z_{1} . z_{2}$

A. -14 - 8i

B. 10 + 11i

C. 10 - 11i

D. –14 + 11i

Xem đáp án

Chọn C.

Ta có:

Câu 5:

Cho số phức $z = (3 - 2 i) {(1 + i)}^{2}$ . Môđun của $w = i z + \bar{z}$ là

A. 2

B. $2 \sqrt{2}$

C. 1

D. $\sqrt{2}$

Xem đáp án

Chọn B.

+) Ta có: (1+i)2 = 1 + 2i + i2 = 2i

Câu 6:

Các số thực x, y thỏa mãn: $(2 x + 3 y + 1) + (- x + 2 y) i = (3 x - 2 y + 2) + (4 x - y - 3) i$ là

A. $(x; y) = (- \frac{9}{11}; - \frac{4}{11})$

B. $(x; y) = (\frac{9}{11}; \frac{4}{11})$

C. $(x; y) = (\frac{9}{11}; - \frac{4}{11})$

D. $(x; y) = (- \frac{9}{11}; \frac{4}{11})$

Xem đáp án

Chọn B.

Câu 7:

Cho số phức $z = 3 + i .$ Điểm biểu diễn số phức $\frac{1}{z}$ trong mặt phẳng phức là:

A. $M (\frac{3}{10}; - \frac{1}{10})$

B. $M (\frac{3}{10}; \frac{1}{10})$

C. $M (\frac{- 3}{10}; - \frac{1}{10})$

D. $M (\frac{- 3}{10}; \frac{1}{10})$

Xem đáp án

Chọn A.

Ta có: z = 3 + i nên

Điểm biểu diễn số phức $\frac{1}{z}$ trong mặt phẳng phức là: $M (\frac{3}{10}; - \frac{1}{10})$

Câu 8:

Cho số phức z thỏa mãn điều kiện: $(1 + i) \bar{z} - 1 - 3 i = 0 .$ Phần ảo của số phức $w = 1 - i z + z$ là

A. 1.

B. –3

C. -2

D. -1

Xem đáp án

Chọn B.

Câu 9:

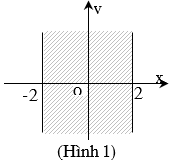
Cho số phức $z = a + b i (a, b \in R) .$ Để điểm biểu diễn của z nằm trong dải (-2;2), ở hình 1, điều kiện của a và b là:

A. $a, b \in (- 2; 2)$

B. $a \in (- 2; 2); b \in ℝ$

C. $a \in ℝ; b \in (- 2; 2)$

D. $a, b \in [- 2; 2]$

Xem đáp án

Chọn B.

Các số phức trong dải đã cho có phần thực trong khoảng (-2;2), phần ảo tùy ý

Câu 10:

Trong C, phương trình $z^{2} + 3 i z + 4 = 0$ có nghiệm là:

A. z = 3i hoặc z = 4i

B. z = 1 + i hoặc z = -3i

C. z = i hoặc z = -4i

D. z = 2- 3i hoặc z = 1 + i

Xem đáp án

Chọn C.

Nếu phương trình có hai nghiệm phức là:

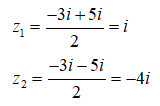
Câu 11:

Tập hợp các điểm biểu diễn số phức z thỏa mãn $| z | < 1$ trên mặt phẳng tọa độ là:

A. Hình tròn tâm O, bán kính R = 1, không kể biên.

B. Hình tròn tâm O, bán kính R = 1, kể cả biên.

C. Đường tròn tâm O, bán kính R = 1.

D. Đường tròn tâm bất kì, bán kính R = 1.

Xem đáp án

Chọn A.

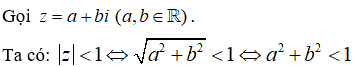
Do đó, tập hợp các điểm biểu diễn số phức z thỏa mãn |z| < 1 là hình tròn tâm O, bán kính R = 1, không kể biên.

Câu 12:

Trong C, phương trình $z^{2} - z + 1 = 0$ có tổng hai nghiệm là:

A. -1

B. 1

C. i

D. –i

Xem đáp án

Chọn B.

Gọi hai nghiệm của phương trình đã cho là z1; z2.

Áp dụng hệ thức Vi-et ta có:

Câu 13:

Xác định tập hợp các điểm M trong mặt phẳng phức biểu diễn các số phức z thỏa mãn điều kiện: $|\bar{z} + 1 - i| \leq 1$

A. Đường tròn tâm I(-1;-1), bán kính R = 1.

B. Hình tròn tâm I(1;-1), bán kính R = 1.

C. Hình tròn tâm I(-1;-1), bán kính R = 1 (kể cả những điểm nằm trên đường tròn).

D. Đường tròn tâm I(1;-1), bán kính R = 1.

Xem đáp án

Chọn C.

Gọi M(x;y) là điểm biểu diễn của số phức z = x + yi trên mặt phẳng phức(x, y ∈ R).

Theo đề bài ta có :

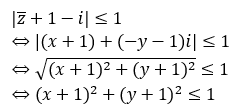
Suy ra, tập hợp các điểm M là hình tròn tâm I(-1;-1) bán kính R = 1 và kể cả đường tròn đó.

Câu 14:

Cho $z = 3 + 4 i .$ Tìm căn bậc hai của z.

A. -2 + i và 2 - i

B. 2 + ivà 2 - i

C. 2 + i và -2 - i

D. $\sqrt{3} + 2 i v à - \sqrt{3} - 2 i$

Xem đáp án

Chọn C.

Giả sử w = x + yi(x, y ∈ R) là một căn bậc hai của số phức z = 3 + 4i.

Ta có:

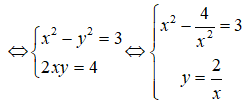
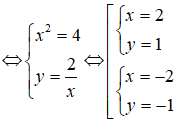
Do đó z có hai căn bậc hai là

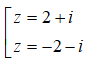
Câu 15:

Phương trình $(2 + i) z^{2} + a z + b = 0 (a, b \in C)$ có hai nghiệm là $3 + i v à 1 - 2 i .$ Khi đó a = ?

A. -9 - 2i

B. 15 + 5i

C. 9 + 2i

D. 15 - 5i

Xem đáp án

Chọn A.

Ta có: z1 = 3 + i; z2 = 1 - 2i là 2 nghiệm của phương trình đã cho và z1 + z2 = 4 - i (1)

Theo Viet, ta có:

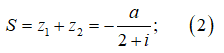
Từ (1) và (2) suy ra:

Câu 16:

Tìm acgumen của số phức: $z = 2 (\sin \frac{π}{5} - i . \cos \frac{π}{5})$

A. $\frac{π}{5} + k 2 π$

B. $\frac{- π}{5} + k 2 π$

C. $\frac{- π}{10} + k 2 π$

D. $\frac{- 3 π}{10} + k 2 π$

Xem đáp án

Chọn D.

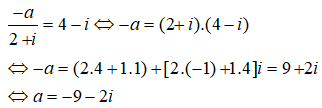
Câu 17:

Cho phương trình $z^{2} + m z - 6 i = 0 .$ Để phương trình có tổng bình phương hai nghiệm bằng 5 thì m có dạng $m = \pm (a + b i) (a, b \in R) . G i á t r ị a + 2 b$ là:

A. 0

B. 1

C. -1

D. –2

Xem đáp án

Chọn C.

Gọi z1, z2 là hai nghiệm của phương trình đã cho

Theo Viet, ta có:

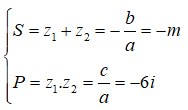
Theo bài cho, tổng bình phương hai nghiệm bằng 5. Ta có:

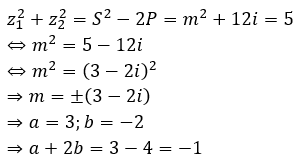
Câu 18:

Cho số phức $z = 1 + i^{2} + i^{4} + . . . + i^{2 n} + . . . + i^{2016}, n \in N .$ Môđun của z bằng?

A. 2.

B. 1.

C. 1008.

D. 2016.

Xem đáp án

Chọn B.

Ta có: z = 1 + i2 + i4 +...+ i2n +...+ i2016, n ∈ N

Là tổng của cấp số nhân có 1009 số hạng, số hạng đầu u1 = 1 và công bội q = i nên:

Lại có:

Câu 19:

Tìm phần ảo của số phức $z = {(1 + i)}^{5}$

A. -4

B. 4

C. 2

D. -2

Xem đáp án

Chọn A.

Do đó, phần ảo của số phức z là – 4.

Câu 20:

Cho hai số phức $z_{1} = 2 - 2 i; z_{2} = \sqrt{3} + i .$ Viết số phức $\frac{z_{1}}{z_{2}}$ dưới dạng lượng giác

A. $\sqrt{2} . \cos (\cos \frac{5 π}{12} + i . \sin \frac{5 π}{12})$

B. $\sqrt{2} . \cos (\cos \frac{5 π}{3} + i . \sin \frac{5 π}{3})$

C. $\sqrt{2} . \cos (\cos \frac{- 5 π}{12} + i . \sin \frac{- 5 π}{12})$

D. Đáp án khác

Xem đáp án

Chọn C

Ta có:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 8 Đề kiểm tra Toán 12 Chương 4 Giải tích có đáp án

Đề kiểm tra 45 phút Toán 12 Chương 4 Giải tích có đáp án (Đề 3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương