200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P9)
-
6536 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số có đồ thị (C) . Biết khoảng cách từ I(-1; 2) đến tiếp tuyến của (C) tại M là lớn nhất thì tung độ của điểm M nằm ở góc phần tư thứ hai, gần giá trị nào nhất?
 Xem đáp án
Xem đáp án
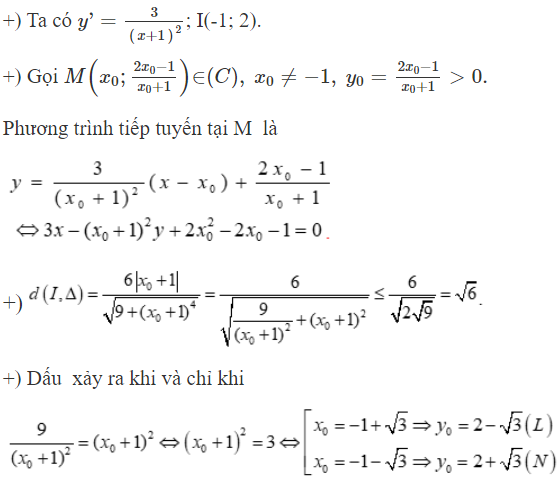
Tung độ này gần với giá trị e nhất trong các đáp án.
Chọn C.
Câu 2:
Cho hàm số có đồ thị (C) . Biết tiếp tuyến tại M của (C) cắt hai tiệm cận của (C) tại A; B sao cho AB ngắn nhất. Khi đó, độ dài lớn nhất của vectơ gần giá trị nào nhất ?
 Xem đáp án
Xem đáp án
Chọn D.
Câu 3:
Viết phương trình tiếp tuyến d của đồ thị (C) : biết d cách đều điểm A( 2; 4) và B( -4; -2).
 Xem đáp án
Xem đáp án
Gọi M( x0; y0) , là tọa độ tiếp điểm của d và (C).
Khi đó d có hệ số góc và có phương trình là :
Vì d cách đều A: B nên d đi qua trung điểm I( -1; 1) của AB hoặc cùng phương với AB .
TH1: d đi qua trung điểm I( -1; 1) , thì ta luôn có:
phương trình này có nghiệm x0= 1
Với x0= 1 ta có phương trình tiếp tuyến
TH2: d cùng phương với AB , tức là d và AB có cùng hệ số góc, khi đó
hay
Với x0 = -2 ta có phương trình tiếp tuyến d: y= x+ 5.
Với x0 =0 ta có phương trình tiếp tuyến d: y = x+ 1.
Vậy, có 3 tiếp tuyến thỏa mãn đề bài:
Chọn D.
Câu 4:
Cho hàm số y= 3x - 4x3 có đồ thị (C). Từ điểm M(1;3) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?
 Xem đáp án
Xem đáp án
+ Đường thẳng đi qua M(1;3) có hệ số góc k có dạng d: y = k(x-1) + 3 .
+ d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:
Thay (2) vào (1) ta được
Vậy có 2 tiếp tuyến.
Chọn C.
Câu 5:
Qua điểm A(0; 2) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x4 - 2x2 + 2
 Xem đáp án
Xem đáp án
Gọi d là tiếp tuyến của đồ thị hàm số đã cho.
Vì nên phương trình của d có dạng: y = kx + 2
Vì d tiếp xúc với đồ thị (C) nên hệ
có nghiệm
Thay (2) vào (1) ta suy ra được
Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
Chọn B.
Câu 6:
Cho hàm số y= x3- 6x2+ 9x -1 có đồ thị là (C) . Từ một điểm bất kì trên đường thẳng x=2 kẻ được bao nhiêu tiếp tuyến đến (C)
 Xem đáp án
Xem đáp án
+ Xét đường thẳng kẻ từ một điểm bất kì trên đường thẳng x = 2 có dạng:
∆: y = k(x - 2) hay y = kx - 2k
+ ∆ là tiếp tuyến của (C)
có nghiệm
+ Phương trình bậc ba có duy nhất một nghiệm tương ứng cho ta một giá trị k . Vậy có một tiếp tuyến.
+ Dễ thấy kẻ từ một điểm bất kì trên đường thẳng x = 2có dạng y = a song song với trục Ox cũng chỉ kẻ được một tiếp tuyến.
Chọn B.
Câu 7:
Tìm m để từ điểm M( 1; 2) kẻ được 2 tiếp tuyến đến đồ thị (C) y= x3 - 2x2+(m-1)x + 2m.
 Xem đáp án
Xem đáp án
Gọi N( x0; y0) thuộc (C). Phương trình tiếp tuyến d tại N là:
Dễ thấy (*) là phương trình hoành độ giao điểm của đồ thị y = 3 - 3m và
Xét hàm số ,
Lập bảng biến thiên, suy ra m = 100/ 81; m = -3
Chọn D.
Câu 8:
Cho hàm số có đồ thị C và điểm A( a; 1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Tổng tất cả giá trị của phần tử S bằng
 Xem đáp án
Xem đáp án
+ Phương trình đường thẳng d đi qua A và có hệ số góc k là : y = k (x-a) + 1
+ Phương trình hoành độ giao điểm của d và C:
Hay kx2+ (-k-ka+2)x - 3 + ka = 0 ( *)
+ Với k = 0 , ta có d: y= 1 là tiệm cận ngang đồ thị hàm số nên không thể tiếp xúc được.
+ Với k ≠ 0, d và C tiếp xúc nhau khi (1) có nghiệm kép
Coi đây là phương trình bậc 2 ẩn k tham số a
+ Để qua A( a; 1)vẽ được đúng tiếp tuyến thì phương trình △x =0 có đúng một nghiệm k ≠ 0.
*Xét 1 - a = 0 hay a = 1, ta có 4k + 4 = 0 hay k = -1 thỏa mãn
*Có f(0) = 4 nên loại đi trường hợp có hai nghiệm trong đó có một nghiệm là 0.
*Còn lại là trường hợp có nghiệm kép khi
Tổng là 1+ 3/2=5/2.
Chọn C.
Câu 9:
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2- 3x+2 cũng là nghiệm của bất phương trình mx2 + (m + 1)x + m + 2 ≥0
 Xem đáp án
Xem đáp án
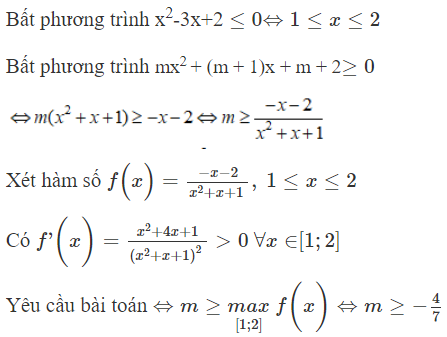
Chọn C.
Câu 10:
Tìm tất cả các giá trị thực của tham số m sao cho phương trình có hai nghiệm thực?
 Xem đáp án
Xem đáp án

Bảng biến thiên
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì
Chọn C.
Câu 11:
Bất phương trình có tập nghiệm (a; b]. Hỏi hiệu b-a có giá trị là bao nhiêu?
 Xem đáp án
Xem đáp án

Chọn A.
Câu 12:
Phương trình có nghiệm thực khi và chỉ khi:
 Xem đáp án
Xem đáp án
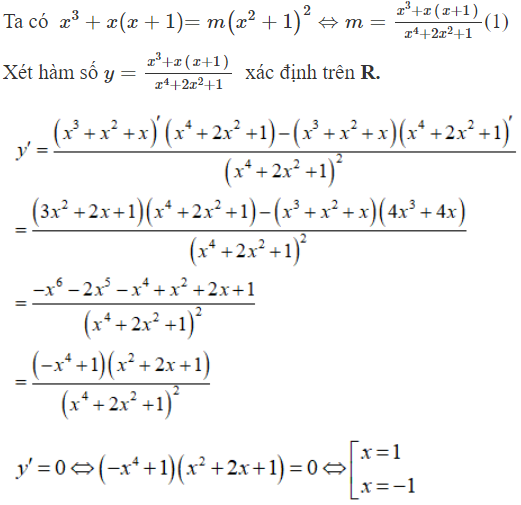
Bảng biến thiên
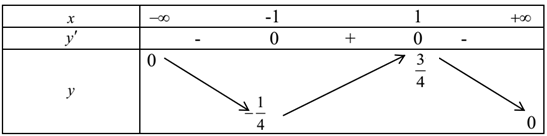
Phương trình (1) có nghiệm thực khi đường thẳng y = m cắt đồ thị hàm số
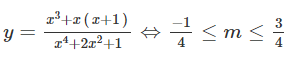
Chọn D.
Câu 13:
Cho hàm số y= f( x) ) liên tục trên R. Hàm số y= f’ (x) có đồ thị như hình vẽ. Hàm số có bao nhiêu cực trị?
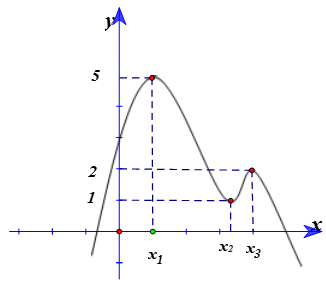
 Xem đáp án
Xem đáp án
Ta có
Suy ra đồ thị của hàm số g’ (x) là phép tịnh tiến đồ thị hàm số y= f’ (x) theo phương Oy xuống dưới ![]() đơn vị.
đơn vị.
Ta có và dựa vào đồ thị của hàm số y= f’ (x), ta suy ra đồ thị của hàm số g’ (x) cắt trục hoành tại 4 điểm.
Chọn D.
Câu 14:
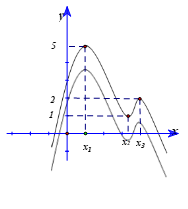
Cho hàm số y= f(x) . Biết f(x) có đạo hàm f’(x) và hàm số y= f’(x) có đồ thị như hình vẽ. Đặt g(x) = f(x+1). Kết luận nào sau đây đúng?
 Xem đáp án
Xem đáp án
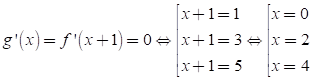
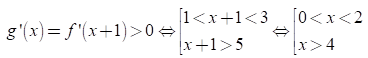
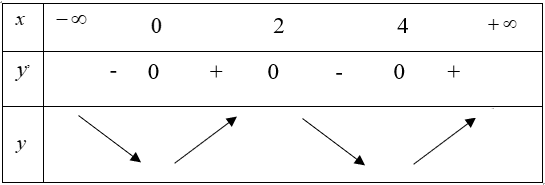
Chọn C.
Câu 15:
Cho hàm số y= f(x) có đạo hàm trên R thoả f( 2) = f( -2) =0 và đồ thị của hàm số y= f’ (x) có dạng như hình bên.
Hàm số y= (f( x)) 2 nghịch biến trên khoảng nào trong các khoảng sau ?
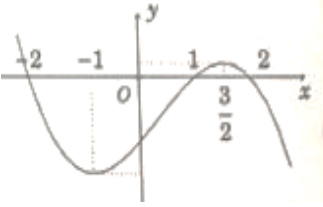
 Xem đáp án
Xem đáp án
Dựa vào đồ thị hàm số ta thấy: f’(x) = 0 khi và chỉ khi x= 1; x=2
Ta có bảng biến thiên :
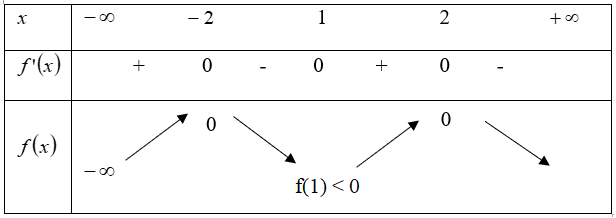
Dựa vào bảng biến thiên ta thấy f(x) < 0 với mọi x ≠ ± 2
Xét hàm số y= (f( x)) 2 có đạo hàm y’ = 2f(x). f’ (x)
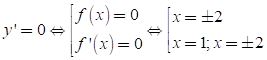
Bảng xét dấu:
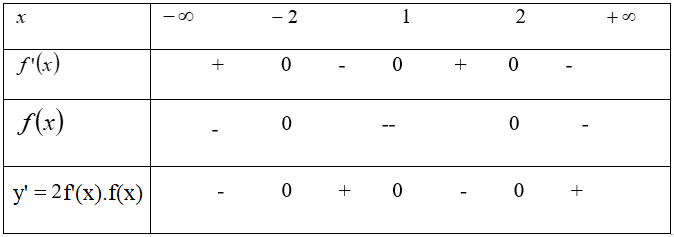
Chọn D.
Câu 16:
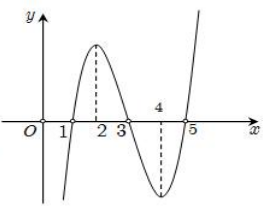
Cho hàm số y= f( x) và đồ thị hình bên là đồ thị của hàm y= f’ ( x) . Hỏi đồ thị của hàm số có tối đa bao nhiêu điểm cực trị ?
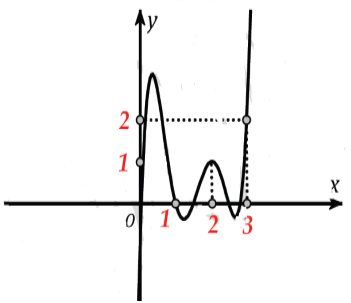
 Xem đáp án
Xem đáp án
Đặt h( x) = 2f( x) – ( x-1) 2
Suy ra đạo hàm: h’( x) = 2f’(x) -2( x-1).
Ta vẽ thêm đường thẳng y= x-1.
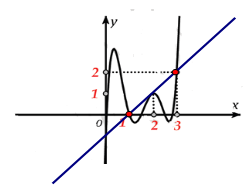
Ta có h’ (x) =0 khi f’(x) =x-1
Suy ra x=0; x=1; x=2; x=3
Theo đồ thị h’(x) > .0 khi f’(x) > x-1
Ta có :
Đồ thị hàm số g( x) có nhiều điểm cực trị nhất khi h( x) có nhiều giao điểm với trục hoành nhất.
Vậy đồ thị hàm số h( x) cắt trục hoành tại nhiều nhất 4 điểm, suy ra đồ thị hàm số g(x) có tối đa 7 điểm cực trị.
Chọn B.
Câu 17:
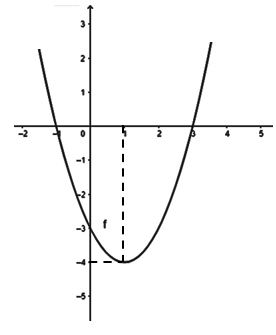
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= -9 tại điểm có hoành độ dương và đồ thị hàm số y= f’ ( x) cho bởi hình vẽ bên. Tìm phần nguyên của giá trị diện tích hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
 Xem đáp án
Xem đáp án
Ta có đạo hàm : f’(x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’(x) ta thấy đồ thị hàm số y= f’ (x) đi qua 3 điểm ( -1; 0) ; (3; 0) ; (1; -4)
Thay tọa độ 3 điểm này vào hàm f’ ta tìm được: a = 1/3; b = -1; c = -3.
Suy ra: f’ (x) = x2-2x-3 và f(x) = 1/3.x3-x2-3x+d.
Do (C) tiếp xúc với đường thẳng y= -9 tại điểm có hoành độ dương nên ta có:
F’(x) =0 khi và chỉ khi x=3 ( x= -1 bị loại vì âm)
Như vậy (C) đi qua điểm (3; -9) ta tìm được d=0.
Vậy hàm số đề bài cho là f(x) = 1/3.x3-x2-3x.
Xét phương trình trình hoành độ giao điểm và trục hoành:
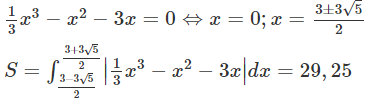
Chọn C.
Câu 18:
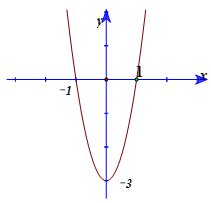
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y= 4 tại điểm có hoành độ âm và đồ thị hàm số y= f’(x) cho bởi hình vẽ bên. Tìm hàm số đã cho ?
 Xem đáp án
Xem đáp án
+ Ta có đạo hàm : f’ (x) = 3ax2+ 2bx+ c.
Dựa vào đồ thị hàm số y= f’( x), ta thấy đồ thị hàm số y= f’ (x) là parabol có trục đối xứng là trục tung nên b=0
Đồ thị hàm số y= f’( x) đi qua 2 điểm (1;0) và (0; -3) thay vào f’(x) ; ta tìm được: a=1 và c= -3.
Suy ra: f’(x) = 3x2-3 và f(x) = x3-3x+d.
+ Do (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm nên ta có:
f’(x) = 0 khi và chỉ khi x = -1 (tm); x = 1 (loại)
Như vậy (C) đi qua điểm (-1; 4) ta tìm được d = 2
Khi đó: f(x) = x3 - 3x + 2.
Chọn A.
Câu 19:
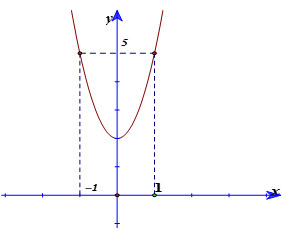
Cho hàm số y=f( x) = ax3+ bx2+ cx+ d có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc toạ độ và đồ thị hàm số y=f’( x) cho bởi hình vẽ bên. Tính f( 3) –f( 1) ?
 Xem đáp án
Xem đáp án
Ta có đạo hàm : f’(x) = 3ax2 + 2bx + c.
Dựa vào đồ thị hàm số y = f’(x) ; ta thấy đồ thị hàm số y = f’(x) là parabol có trục đối xứng là trục tung nên b = 0
+ Đồ thị hàm số y = f’(x) đi qua 2 điểm (1; 5) và (0; 2) ta tìm được: a = 1 và c = 2.
Suy ra: f’(x) = 3x2+ 2 và f( x) = x3 + 2x + d,
+ Do đồ thị hàm số (C) đi qua gốc toạ độ nên 0 = 0 + 0 + d
Suy ra: d = 0.
Khi đó ta có: f(x) = x3 + 2x và f(3) – f(2) = 21
Chọn D.
Câu 20:
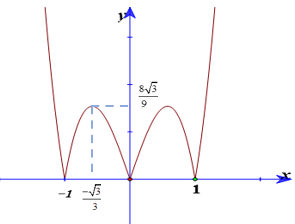
Cho hàm số y = f(x) = ax4 + bx2 + c (a > 0) có đồ thị (C), đồ thị hàm số y = f’(x). Đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
 Xem đáp án
Xem đáp án
+ Từ đồ thị của hàm số và a > 0 ta dễ dàng có được đồ thị hàm số y = f’(x) như sau:
Ta có : f’(x) = 4ax3 + 2bx
Đồ thị hàm số y = f’(x) đi qua ta tìm được a = 1 và b = -2
Suy ra hàm số đã cho có dạng: f(x) = x4 - 2x2 + d và f’(x) = 4x3 - 4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x = 0; x = 1; x = -1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) = 1 suy ra 1= 0 - 2.0 + d nên d = 1
Vậy hàm số cần tìm là: y = x4 - 2x2 + 1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4 - 2x2 + 1 = 0 nên x = ±1
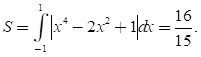
Chọn D.
