Bài tập Bài 2. Xác suất của biến cố có đáp án
-
193 lượt thi
-
21 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Lấy ngẫu nhiên đồng thời 2 viên bi từ một hộp có chứa 5 bi xanh và 5 bi đỏ có cùng kích thước và trọng lượng. Biến cố lấy được 2 viên bi cùng màu hay 2 viên bi khác màu có khả năng xảy ra cao hơn? Trong bài này ta sẽ tìm hiểu công thức tính xác suất để có thể so sánh được khả năng xảy ra của hai biến cố trên.
 Xem đáp án
Xem đáp án
Sau khi học xong bài 2. Xác suất của biến cố, ta sẽ giải bài này như sau:
Khi lấy ra ngẫu nhiên đồng thời hai viên bi từ một hộp có chứa 5 bi xanh và 5 bi đỏ có cùng kích thước và trọng lượng, ta có ![]() = 45 cách.
= 45 cách.
⇒ n(Ω) = 45.
Gọi A là biến cố: “Lấy được hai viên bi cùng màu”.
Khi đó ta lấy được 2 viên bi xanh hoặc lấy được 2 viên bi đỏ.
Lấy được 2 viên bi xanh có: = 10 cách.
Lấy được 2 viên bi đỏ có: = 10 cách.
Theo quy tắc cộng, ta có + = 10 + 10 = 20 cách lấy hai viên bi cùng màu.
⇒ Số khả năng thuận lợi cho A là: n(A) = 20.
⇒ Xác suất của biến cố A là: P(A) = .
Gọi B là biến cố “Lấy được hai viên bi khác màu”.
Khi đó ta lấy được 1 viên bi màu xanh và 1 viên bi màu đỏ.
Lấy 1 viên bi màu xanh có = 5 cách
Lấy 1 viên bi màu đỏ có = 5 cách
Theo quy tắc nhân, ta có = 5.5 = 25 cách lấy hai viên bi khác màu.
⇒ Số khả năng thuận lợi cho B là: n(B) = 25.
⇒ Xác suất của biến cố B là: P(B) =
Ta có: < ⇒ P(A) < P(B)
⇒ Biến cố lấy được hai viên bi khác màu có khả năng xảy ra cao hơn.
Vậy biến cố lấy được hai viên bi khác màu có khả năng xảy ra cao hơn.
Câu 2:
Gieo một con xúc xắc cân đối và đồng chất. Hãy so sánh khả năng xảy ra của hai biến cố
A: “Mặt xuất hiện có số chấm là số chẵn”;
B: “Mặt xuất hiện có số chấm là số lẻ”.
 Xem đáp án
Xem đáp án
Xúc xắc cân đối và đồng chất nên khi gieo thì ta có các kết quả có thể là: 1; 2; 3; 4; 5; 6 chấm xuất hiện.
⇒ Không gian mẫu của phép thử trên là: Ω = {1; 2; 3; 4; 5; 6}
Tập hợp các kết quả thuận lợi cho biến cố A là:
A = {2; 4; 6} ⇒ Có 3 kết quả thuận lợi cho biến cố A.
Tập hợp các kết quả thuận lợi cho biến cố B là:
B = {1; 3; 5} ⇒ Có 3 kết quả thuận lợi cho biến cố B.
Vì vậy khả năng xảy ra của hai biến cố là như nhau.
Câu 3:
Gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất của các biến cố:
a) “Hai mặt xuất hiện có cùng số chấm”;
 Xem đáp án
Xem đáp án
Kết quả của phép thử là cặp số (i;j), trong đó i và j lần lượt là số chấm xuất hiện trên con xúc xắc thứ nhất và thứ hai.
Không gian mẫu là:
Ω = {(1; 1), (1; 2), (1; 3), (1; 4), (1; 5), (1; 6), (2; 1), (2; 2), (2; 3), (2; 4), (2; 5), (2; 6), (3; 1), (3; 2), (3; 3), (3; 4), (3; 5); (3; 6), (4; 1), (4; 2), (4; 3), (4; 4), (4; 5), (4; 6), (5; 1), (5; 2), (5; 3), (5; 4), (5; 5), (5; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5), (6; 6)}.
Khi đó, số phần tử của không gian mẫu là: n(Ω) = 36
a) Gọi A là biến cố “Hai mặt xuất hiện cùng số chấm”.
Ta có A = {(1; 1), (2; 2), (3; 3), (4; 4), (5; 5), (6; 6)}
⇒ Số các kết quả thuận lợi cho A là n(A) = 6. Do đó, xác suất của biến cố A là:
P(A) = .
Vậy xác suất của các biến cố “Hai mặt xuất hiện có cùng số chấm” là .
Câu 4:
b) “Tổng số chấm trên hai mặt xuất hiện bằng 9”.
 Xem đáp án
Xem đáp án
b) Gọi B là biến cố “Tổng số chấm trên hai mặt xuất hiện bằng 9”.
Ta có: B = {(6; 3), (5; 4), (3; 6), (4; 5)}.
⇒ Số các kết quả thuận lợi cho B là n(B) = 4.
Do đó, xác suất của biến cố B là: P(B) = .
Vậy xác suất của biến cố “Tổng số chấm trên hai mặt xuất hiện bằng 9” là .
Câu 5:
Hãy tính xác suất của hai biến cố được nêu ra ở hoạt động khởi động của bài học.
 Xem đáp án
Xem đáp án
Khi lấy ra ngẫu nhiên đồng thời hai viên bi từ một hộp có chứa 5 bi xanh và 5 bi đỏ có cùng kích thước và trọng lượng, ta có ![]() = 45 cách.
= 45 cách.
⇒ n(Ω) = 45.
Gọi A là biến cố: “Lấy được hai viên bi cùng màu”.
Khi đó ta lấy được 2 viên bi xanh hoặc lấy được 2 viên bi đỏ.
Lấy được 2 viên bi xanh có: = 10 cách.
Lấy được 2 viên bi đỏ có: = 10 cách.
Theo quy tắc cộng, ta có + = 10 + 10 = 20 cách lấy hai viên bi cùng màu.
⇒ Số khả năng thuận lợi cho A là: n(A) = 20.
⇒ Xác suất của biến cố A là: P(A) =.
Gọi B là biến cố “Lấy được hai viên bi khác màu”.
Khi đó ta lấy được 1 viên bi màu xanh và 1 viên bi màu đỏ.
Lấy 1 viên bi màu xanh có = 5 cách
Lấy 1 viên bi màu đỏ có = 5 cách
Theo quy tắc nhân, ta có = 5.5 = 25 cách lấy hai viên bi khác màu.
⇒ Số khả năng thuận lợi cho B là: n(B) = 25.
⇒ Xác suất của biến cố B là: P(B) =
Ta có: < ⇒ P(A) < P(B)
⇒ Biến cố lấy được hai viên bi khác màu có khả năng xảy ra cao hơn.
Vậy biến cố lấy được hai viên bi khác màu có khả năng xảy ra cao hơn.
Câu 6:
Ba bạn Lan, Mai, Đào đặt thẻ học sinh của mình vào một hộp kín, sau đó mỗi bạn lấy ngẫu nhiên một thẻ từ hộp. Tính xác suất của biến cố “Không bạn nào lấy đúng thẻ của mình”.
 Xem đáp án
Xem đáp án
Gọi A là biến cố “Không bạn nào lấy đúng thẻ của mình”.
Các kết quả có thể xảy ra được thể hiện ở sơ đồ sau:
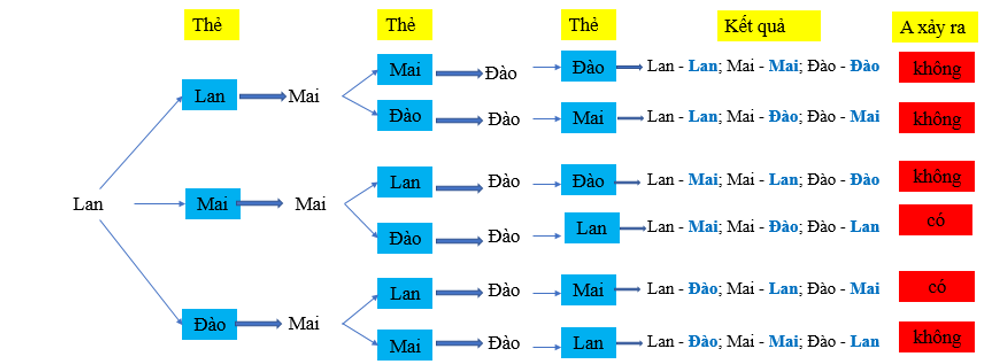
Từ sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho A.
Do đó P(A) = .
Vậy xác suất của biến cố “Không bạn nào lấy đúng thẻ của mình” là .
Câu 7:
Một hộp có 10 tấm thẻ giống nhau được đánh số lần lượt từ 1 đến 10. Chọn ra ngẫu nhiên cùng một lúc 3 thẻ. Tính xác suất biến cố tích các số ghi trên 3 thẻ đó là số chẵn.
 Xem đáp án
Xem đáp án
Trong các số từ 1 đến 10 có 5 số chẵn và 5 số lẻ.
Chọn ra ngẫu nhiên cùng một lúc 3 thẻ nên ta có số phần tử của không gian mẫu là: n(Ω) = = 120 (phẩn tử).
Gọi A là biến cố “Tích các số ghi trên 3 thẻ là số chẵn”; B là là biến cố “Tích các số ghi trên 3 thẻ là số lẻ”.
Ta có tích của ba số lẻ là một số lẻ. Khi đó để B xảy ra thì ba số được chọn phải là số lẻ.
Khi đó, ta chọn 3 trong 5 số lẻ ⇒ n(B) = = 10 (phần tử).
⇒ Xác suất để biến cố B xảy ra là: P(B) = .
Nếu cả 3 số được chọn không phải là số lẻ thì tích ba số cho ta một số chẵn.
Khi đó, ta có các trường hợp còn lại của không gian mẫu thuận lợi cho biến cố A xảy ra.
Suy ra: số phần tử của biến cố A là n(A) = n(Ω) – n(B) = 120 – 10 = 110 (phần tử).
⇒ Xác suất để biến cố A xảy ra là: P(A) =.
Vậy xác suất của biến cố tích các số ghi trên 3 thẻ là số chẵn là .
Câu 8:
Gieo đồng thời ba con xúc xắc cân đối và đồng nhất. Tính xác suất của các biến cố:
a) “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc chia hết cho 3”;
 Xem đáp án
Xem đáp án
Khi gieo đồng thời 3 con xúc xắc thì mỗi con xúc xắc có thể xuất hiện một trong 6 mặt từ mặt 1 chấm đến 6 chấm.
Khi đó số kết quả có thể xảy ra của phép thử là: n(Ω) = 63 = 216.
a) Gọi A là biến cố “Tích các số chấm xuất hiện trên ba con xúc xắc chia hết cho 3”
⇒ Biến cố đối của biến cố A là : “Tích các số chấm xuất hiện trên ba con xúc xắc không chia hết cho 3”.
Để tích của số chấm trên ba con xúc xắc không chia hết cho 3 thì khi kết quả không xuất hiện mặt 3 chấm và 6 chấm.
Tức là số chấm xuất hiện trên ba con xúc xắc phải là {1; 2; 4; 5}.
⇒ Số kết quả thuận lợi cho là: n() = 43 = 64.
⇒ P() =
⇒ Xác suất của biến cố A là: P(A) = 1 – P() = 1 – .
Vậy xác suất biến cố “Tích các số chấm ở mặt xuất hiện trên ba con xúc xắc chia hết cho 3” là .
Câu 9:
b) “Tổng các số chấm ở mặt xuất hiện trên ba con xúc xắc lớn hơn 4”.
 Xem đáp án
Xem đáp án
b) Gọi B là biến cố “Tổng các số chấm xuất hiện trên mặt ba con xúc xắc lớn 4”.
⇒ Biến cố đối của biến cố B là : “Tổng các số chấm xuất hiện trên mặt ba con xúc xắc nhỏ hơn hoặc bằng 4”.
Vì xúc xắc có số chấm nhỏ nhất là 1 nên tổng số chấm xuất hiện trên ba con xúc xắc phải lớn hơn hoặc bằng 3.
Ta có: 3 = 1 + 1 + 1; 4 = 1 + 1 + 2 = 1 + 2 + 1 = 2 + 1 + 1
⇒ Có 4 kết quả để tung ba con xúc xắc cho tổng nhỏ hơn hoặc bằng 4 ⇒ n() = 4
⇒ P() =
⇒ Xác xuất của biến cố B là: P(B) = 1 – P() = 1 – = .
Vậy xác suất của biến cố: “Tổng các số chấm ở mặt xuất hiện trên ba con xúc xắc lớn hơn 4” là .
Câu 10:
Trong hộp có 3 bi xanh, 4 bi đỏ và 5 bi vàng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên từ trong hộp 4 viên bi. Tính xác suất để trong 4 bi lấy ra:
a) Có ít nhất 1 bi xanh.
 Xem đáp án
Xem đáp án
a) Ta có tổng số bi gồm 3 bi xanh, 4 bi đỏ và 5 bi vàng là 3 + 4 + 5 = 12 viên bi.
Lấy ngẫu nhiên 4 viên bi trong tổng số 12 viên bi có = 495 cách.
⇒ Số phần tử của không gian mẫu là: n(Ω) = 495.
Gọi A là biến cố “Không lấy được bi xanh nào”. Khi đó, số bi lấy ra chỉ có bi đỏ và vàng.
Tức là lấy 4 viên bi từ 9 viên bi (4 bi đỏ và 5 bi vàng), ta có = 126 cách.
⇒ n(A) = 126.
⇒ Xác suất để xảy ra biến cố A là: P(A) = .
Biến cố : “Trong 4 bi lấy ra có ít nhất 1 bi xanh” là biến cố đối của biến cố A.
Khi đó, xác suất để xảy ra biến cố “Trong 4 bi lấy ra có ít nhất 1 bi xanh là”:
P() = 1 – P(A) = 1 – = .
Vậy xác suất để trong 4 bi lấy ra có ít nhất 1 bi xanh là .
Câu 11:
b) Có ít nhất 2 bi đỏ.
 Xem đáp án
Xem đáp án
b) Gọi B là biến cố “Lấy được ít nhất 2 bi đỏ”.
⇒ Biến cố đối của biến cố B là : “Lấy được 1 viên bi đỏ hoặc không lấy được viên bi đỏ nào”.
- Lấy được 1 viên bi đỏ còn 3 viên bi là xanh hoặc vàng, ta có: = 224 cách.
- Không lấy được viên bi màu đỏ nào, tức là lấy được 4 viên bi trong 8 viên bi xanh và vàng, ta có: = 70 cách.
Theo quy tắc cộng ta có số cách để lấy được 1 viên bi đỏ hoặc không lấy được viên bi đỏ nào là 224 + 70 = 294.
⇒ n() = 294
⇒ P() = .
⇒ P(B) = 1 – P() = 1 – .
Vậy xác suất để trong 4 bi lấy ra có ít nhất 2 bi đỏ là: .
Câu 12:
Có một hạt gạo nếp nằm lẫn trong một cái thùng chứa 10 kg gạo tẻ. Lấy ngẫu nhiên một hạt gạo từ thùng. Theo bạn, hạt gạo lấy ra là gạo tẻ hay gạo nếp?
 Xem đáp án
Xem đáp án
Vì trong một thùng 10 kg gạo tẻ chỉ có 1 hạt gạo nếp, nghĩa là trong vô số hạt gạo tẻ chỉ có 1 hạt gạo nếp.
Vì vậy, xác suất của biến cố “ Hạt gạo lấy ra là gạo nếp” rất nhỏ, gần như bằng 0.
Vậy hạt gạo lấy ra là gạo tẻ.
Câu 13:
Tung ba đồng xu cân đối và đồng chất. Xác định biến cố đối của mỗi biến cố sau và tính xác suất của nó.
a) “Xuất hiện ba mặt sấp”;
 Xem đáp án
Xem đáp án
a) Gọi A là biến cố “Xuất hiện ba mặt sấp”.
Biến cố A không xảy ra khi không xuất hiện ba mặt sấp, nghĩa là xuất hiện ít nhất một mặt ngửa.
Do đó, biến cố đối của biến cố A là : “Xuất hiện ít nhất một mặt ngửa”.
Khi tung một đồng xu cân đối và đồng chất thì có 2 khả năng có thể là xuất hiện mặt sấp (S) hoặc xuất hiện mặt ngửa (N).
Khi đó tung ba đồng xu cân đối và đồng chất thì có 2.2.2 = 8 khả năng.
⇒ Số phần tử của không gian mẫu là: n(Ω) = 8.
A là biến cố “Xuất hiện ba mặt sấp” ⇒ A = {SSS} ⇒ n(A) = 1.
⇒ P(A) = .
⇒ P() = 1 – P(A) = 1 – = .
Vậy xác suất của biến cố: “Xuất hiện ba mặt sấp” là ; xác suất của biến cố: “Xuất hiện ít nhất một mặt ngửa” là .
Câu 14:
b) “Xuất hiện ít nhất một mặt sấp”.
 Xem đáp án
Xem đáp án
b) Gọi B là biến cố “Xuất hiện ít nhất một mặt sấp”.
⇒ Biến cố đối của biến cố B là “Xuất hiện ba mặt ngửa”, tức là : “Xuất hiện ba mặt ngửa”.
Ta có: = {NNN} ⇒ n() = 1⇒ P() = = .
⇒ P(B) = 1 – P() = 1 – = .
Vậy xác suất của biến cố “Xuất hiện ít nhất một mặt sấp” là ; xác suất của biến cố “Xuất hiện ba mặt ngửa” là ;
Câu 15:
Gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất của mỗi biến cố sau:
a) “Tổng số chấm nhỏ hơn 10”;
 Xem đáp án
Xem đáp án
Gieo một con xúc xắc cân đối và đồng chất thì có 6 kết quả có thể.
Khi đó, gieo hai con xúc xắc cân đối và đồng chất thì có 6.6 = 36 kết quả có thể.
⇒ Số phần tử của không gian mẫu là: n(Ω) = 6. 6 = 36.
a) Gọi A là biến cố “Tổng số chấm nhỏ hơn 10”.
⇒ Biến cố đối của biến cố A là : “Tổng số chấm lớn hơn hoặc bằng 10”.
⇒ = {(4; 6), (5; 5), (5; 6), (6; 4), (6; 5), (6; 6)}
⇒ n() = 6 ⇒ P() = .
⇒ Xác suất xảy ra biến cố A là: P(A) = 1 – P() = 1 – = .
Vậy xác suất xảy ra biến cố “Tổng số chấm nhỏ hơn 10” là .
Câu 16:
b) “Tích số chấm xuất hiện chia hết cho 3”.
 Xem đáp án
Xem đáp án
b) Gọi B là biến cố “Tích số chấm xuất hiện chia hết cho 3”.
⇒ Biến cố đối của biến cố B là “Tích số chấm xuất hiện không chia hết cho ba”.
Để tích số chấm không chia hết cho ba thì kết quả sau khi gieo xúc xắc không được xuất hiện mặt 3 và 6.
Khi đó, số chấm của hai con xúc xắc phải thuộc: {1; 2; 4; 5}.
⇒ Số phần tử thuận lợi cho biến cố là: n() = 42 = 16
⇒ P() =
⇒ Xác suất của biến cố B là: P(B) = 1 – P( ) = 1 – .
Vậy xác suất của biến cố “Tích số chấm xuất hiện chia hết cho 3” là .
Câu 17:
Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.
a) Sử dụng sơ đồ hình cây, liệt kê tất cả các kết quả có thể xảy ra.
 Xem đáp án
Xem đáp án
a) Các kết quả có thể xảy ra khi lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ được thể hiện ở sơ đồ cây sau:
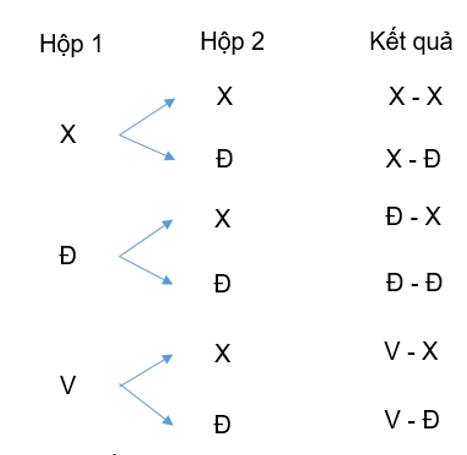
Vậy có tất cả 6 kết quả có thể xảy ra là: Ω = {xanh - xanh, xanh - đỏ, đỏ - xanh, đỏ - đỏ, vàng - xanh, vàng - đỏ}.
Câu 18:
b) Tính xác suất của biến cố “Trong hai thẻ lấy ra có ít nhất một thẻ đỏ”.
 Xem đáp án
Xem đáp án
b) Gọi A là biến cố “Trong hai thẻ lấy ra có ít nhất một thẻ màu đỏ”.
Khi đó, các kết quả thuận lợi cho A là xanh - đỏ, đỏ - xanh, đỏ - đỏ, vàng - đỏ.
⇒ A = {xanh - đỏ, đỏ - xanh, đỏ - đỏ, vàng - đỏ}
⇒ n(A) = 4
⇒ P(A) =.
Vậy xác suất của biến cố “Trong hai thẻ lấy ra có ít nhất một thẻ đỏ” là
Câu 19:
Trong hộp có một số quả bóng màu xanh và màu đỏ có kích thước và khối lượng như nhau. An nhận thấy nếu lấy ngẫu nhiên hai quả bóng từ hộp thì xác xuất để hai quả này khác màu là 0,6. Hỏi xác xuất để hai quả bóng lấy ra cùng màu là bao nhiêu.
 Xem đáp án
Xem đáp án
Vì biến cố “Lấy được hai quả bóng cùng màu” là biến cố đối của biến cố “Lấy được hai quả bóng khác màu”.
Do đó, xác xuất để hai quả bóng lấy ra cùng màu là: 1 – 0, 6 = 0,4.
Vậy xác xuất để hai quả bóng lấy ra cùng màu là 0,4.
Câu 20:
Năm bạn Nhân, Lễ, Nghĩa, Trí và Tín xếp hàng một cách ngẫu nhiên thành một hàng ngang để chụp ảnh. Tính xác suất của biến cố:
a) “Nhân và Tín không đứng cạnh nhau”;
 Xem đáp án
Xem đáp án
a) Năm bạn Nhân, Lễ, Nghĩa, Trí và Tín xếp hàng một cách ngẫu nhiên thành một hàng ngang, ta có 5! = 120 cách xếp.
⇒ Số phần tử của không gian mẫu là: n(Ω) = 120.
Gọi A là biến cố “Nhân và Tín đứng cạnh nhau”.
Coi Nhân và Tín là một nhóm thì có 2! cách sắp xếp hai bạn này trong nhóm. Xếp nhóm Nhân và Tín với 3 người còn lại thì có 4! cách sắp xếp.
Theo quy tắc nhân ta có 2!. 4! = 48 cách xếp sao cho Nhân và Tín đứng cạnh nhau.
⇒ Số các kết quả thuận lợi cho A là: n(A) = 2!. 4! = 48.
⇒ Xác suất của biến cố A là: P(A) = .
Mặt khác, biến cố :“Nhân và Tín không đứng cạnh nhau” và biến cố A :“Nhân và Tín đứng cạnh nhau” là hai biến cố đối nhau.
⇒ Xác suất của biến cố “Nhân và Tín không đứng cạnh nhau” là:
P() = 1 – P(A) = 1 – .
Vậy xác suất của biến cố “Nhân và Tín không đứng cạnh nhau” là .
Câu 21:
b) “Trí không đứng ở đầu hàng”.
 Xem đáp án
Xem đáp án
b) Gọi B là biến cố “Trí đứng ở đầu hàng”.
Khi đó biến cố đối của B là : “Trí không đứng ở đầu hàng”.
Khi Trí đứng ở đầu hàng (có thể là đầu hàng bên trái hoặc đầu hàng bên phải), ta có 2 cách sắp xếp Trí và 4! cách sắp xếp 4 người còn lại.
Theo quy tắc nhân ta có 2. 4! = 48 cách xếp sao cho Trí đứng ở đầu hàng.
⇒ n(B) = 48.
⇒ P(B) = .
⇒ P() = 1 – P(B) = 1 – .
Vậy, xác suất của biến cố “Trí không đứng ở đầu hàng” là .
