15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 4. Ba đường conic trong mặt phẳng tọa độ có đáp án

Câu 1:

Cho elip (E): $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ . Trong các khẳng định sau, khẳng định nào sai?

A. (E) có các tiêu điểm F₁(–4; 0) và F₂(4; 0);

B. (E) có tỉ số $\frac{c}{a} = \frac{4}{5}$ ;

C. (E) có đỉnh A₁(–5; 0);

D. (E) có độ dài trục nhỏ bằng 3.

Xem đáp án

Đáp án đúng là: D

• Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , với a² = 25, b² = 9.

Ta suy ra a = 5, b = 3 (vì a, b > 0).

Ta có b = $\sqrt{a^{2} - c^{2}}$

⇔ b² = a² – c²

⇔ c² = a² – b² = 25 – 9 = 16.

⇔ c = 4.

Vậy các tiêu điểm của elip (E) là: F₁(–4; 0), F₂(4; 0).

Do đó phương án A đúng.

• Ta có tỉ số $\frac{c}{a} = \frac{4}{5}$

Do đó phương án B đúng.

• Đỉnh A₁(–a; 0).

Suy ra A₁(–5; 0).

Do đó phương án C đúng.

• Độ dài trục nhỏ là 2b = 2.3 = 6 ≠ 3.

Do đó phương án D sai.

Vậy ta chọn phương án D.

Câu 2:

Cho hypebol (H): 4x² – y² = 1. Khẳng định nào sau đây đúng?

A. Hypebol có tiêu cự bằng $\frac{\sqrt{5}}{2}$ ;

B. Hypebol có một tiêu điểm là $F (\sqrt{5}; 0)$ ;

C. Hypebol có trục thực bằng 1;

D. Hypebol có trục ảo bằng 1/2

Xem đáp án

Đáp án đúng là: C

Ta có 4x² – y² = 1.

Suy ra $\frac{x^{2}}{\frac{1}{4}} - \frac{y^{2}}{1} = 1$

Hay $\frac{x^{2}}{{(\frac{1}{2})}^{2}} - \frac{y^{2}}{1^{2}} = 1$

Khi đó ta có a = 1/2, b = 1.

• Ta có $b = \sqrt{c^{2} - a^{2}}$

Suy ra $c = \sqrt{b^{2} + a^{2}} = \sqrt{1 + \frac{1}{4}} = \frac{\sqrt{5}}{2}$

Vậy hypebol (H) có tiêu cự là 2c = $\sqrt{5} \neq \frac{\sqrt{5}}{2}$

Do đó phương án A sai.

• Ta có $c = \frac{\sqrt{5}}{2}$

Suy ra hai tiêu điểm của (H) là $F_{1} (- \frac{\sqrt{5}}{2}; 0), F_{2} (\frac{\sqrt{5}}{2}; 0)$

Do đó phương án B sai.

• Ta có trục thực là: A₁A₂ = 2a = 2.1/2 = 1.

Do đó phương án C đúng.

• Ta có trục ảo là: 2b = 2.1 = 2 ≠ 1/2.

Do đó phương án D sai.

Vậy ta chọn phương án C.

Câu 3:

Cho parabol (P): y² = 16x. Khẳng định nào sau đây sai?

A. (P) có tiêu điểm F(4; 0);

B. (P) có tọa độ đỉnh O(0; 0);

C. Phương trình đường chuẩn ∆: x = 4;

D. (P) nhận Ox làm trục đối xứng.

Xem đáp án

Đáp án đúng là: C

• Ta có (P): y² = 16x nên 2p = 16.

Suy ra p = 8.

Do đó $\frac{p}{2} = \frac{8}{2} = 4$

Vì vậy (P) có tiêu điểm F(4; 0).

Do đó phương án A đúng.

• Ta có O(0; 0) là đỉnh của parabol (P) và Ox là trục đối xứng của parabol (P).

Do đó phương án B, D đúng.

Đến đây ta có thể chọn đáp án C.

• Phương trình đường chuẩn ∆ có dạng: $x = - \frac{p}{2} = - 4$ .

Do đó phương án C sai.

Vậy ta chọn phương án C.

Câu 4:

Elip có tỉ số giữa độ dài trục nhỏ và tiêu cự bằng $\sqrt{2}$ , tổng bình phương độ dài trục lớn và tiêu cự bằng 64. Phương trình chính tắc của elip là:

A. $\frac{x^{2}}{12} + \frac{y^{2}}{8} = 1$

B. $\frac{x^{2}}{8} + \frac{y^{2}}{12} = 1$

C. $\frac{x^{2}}{12} + \frac{y^{2}}{4} = 1$

D. $\frac{x^{2}}{8} + \frac{y^{2}}{4} = 1$

Xem đáp án

Đáp án đúng là: A

Ta có tỉ số giữa độ dài trục nhỏ và tiêu cự bằng $\sqrt{2}$ .

Suy ra $\frac{2 b}{2 c} = \sqrt{2}$

$\Leftrightarrow b = c \sqrt{2} \Leftrightarrow \sqrt{a^{2} - c^{2}} = c \sqrt{2}$

⇔ a² – c² = 2c²

⇔ a² = 3c².

Lại có tổng bình phương độ dài trục lớn và tiêu cự bằng 64.

Ta suy ra (2a)² + (2c)² = 64.

⇔ 4a² + 4c² = 64.

⇔ a² + c² = 16.

⇔ 3c² + c² = 16.

⇔ 4c² = 16.

⇔ c² = 4.

⇔ c = 2 (vì c > 0).

Với c = 2, ta có:

• a² = 3c² = 3.2² = 12.

• b = $c \sqrt{2} = 2 \sqrt{2}$

Suy ra b² = 8.

Vậy phương trình elip cần tìm là: $\frac{x^{2}}{12} + \frac{y^{2}}{8} = 1$

Do đó ta chọn phương án A.

Câu 5:

Hypebol có độ dài trục thực gấp đôi độ dài trục ảo và có tiêu cự bằng . Phương trình chính tắc của hypebol là:

A. $\frac{x^{2}}{48} - \frac{y^{2}}{12} = 1$

B. $\frac{x^{2}}{12} - \frac{y^{2}}{48} = 1$

C. $\frac{x^{2}}{48} + \frac{y^{2}}{12} = 1$

D. $\frac{x^{2}}{48} + \frac{y^{2}}{12} = 1$

Xem đáp án

Đáp án đúng là: A

Theo đề, ta có độ dài trục thực gấp đôi độ dài trục ảo

Ta suy ra 2a = 2.2b.

Do đó a = 2b.

Hypebol có tiêu cự bằng $4 \sqrt{15}$ .

Ta suy ra 2c = $4 \sqrt{15}$ .

Do đó $c = 2 \sqrt{15}$ .

$\Leftrightarrow \sqrt{a^{2} + b^{2}} = 2 \sqrt{15}$

⇔ 4b² + b² = 60.

⇔ 5b² = 60.

⇔ b² = 12.

$\Leftrightarrow b = 2 \sqrt{3}$

Suy ra $a^{2} = 48$

Vậy ta có phương trình chính tắc của hypebol là:

$\frac{x^{2}}{48} - \frac{y^{2}}{12} = 1$

Do đó ta chọn phương án A.

Câu 6:

Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường parabol?

A. $\frac{x^{2}}{8} + \frac{y^{2}}{24} = 1$

B. y² = 2x;

C. $\frac{x^{2}}{64} - \frac{y^{2}}{49} = 1$

D. x² = 21y.

Xem đáp án

Đáp án đúng là: B

Phương trình parabol có dạng: y² = 2px.

Ta thấy chỉ có phương trình của đáp án B có dạng phương trình parabol trên.

Vậy ta chọn phương án B.

Câu 7:

Cho elip (E): $\frac{x^{2}}{169} + \frac{y^{2}}{144} = 1$ . Nếu điểm M nằm trên (E) có hoành độ bằng –13 thì độ dài MF₁ và MF₂ lần lượt là:

A. 10 và 6;

B. 8 và 18;

C. $13 \pm \sqrt{5}$

D. $13 \pm \sqrt{10}$

Xem đáp án

Đáp án đúng là: B

Phương trình elip (E) có dạng: $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ , với a = 13, b = 12.

Ta có $c = \sqrt{a^{2} - b^{2}} = \sqrt{169 - 144} = 5$

Khi đó F₁(–5; 0) và F₂(5; 0).

Với M(x_M; y_M) ta có: $\vec{F_{1} M} = (x_{M} + 5; y_{M}) n ê n F_{1} M = \sqrt{{(x_{M} + 5)}^{2} + y_{M}^{2}} F_{1} M = \sqrt{{(x_{M} + 5)}^{2} + 144. (1 - \frac{x_{M}^{2}}{169})} F_{1} M = \sqrt{169 + 10 x_{M} + \frac{25}{169} x_{M}^{2}} F_{1} M = \sqrt{{(13 + \frac{5}{13} x_{M})}^{2}} F_{1} M = 13 + \frac{5}{13} x_{M}$

(do F₁M > 0).

Tương tự ta có $F_{2} M = 13 - \frac{5}{13} x_{M}$

Mà theo bài x_M = –13 nên ta có:

• MF₁ = $13 + \frac{5}{13} . (- 13) = 8$

• MF₂ = $13 - \frac{5}{13} . (- 13) = 18$

Do đó ta chọn phương án B.

Câu 8:

Cho hypebol (H): $\frac{x^{2}}{36} - \frac{y^{2}}{9} = 1$ . Tỉ số giữa độ dài trục ảo và độ dài trục thực bằng:

A. 2;

B. 1/2

C. $\frac{\sqrt{5}}{2}$

D. $\frac{2 \sqrt{5}}{5}$

Xem đáp án

Đáp án đúng là: B

(H): $\frac{x^{2}}{36} - \frac{y^{2}}{9} = 1$

Ta có a = 6, b = 3.

Suy ra:

⦁ Độ dài trục ảo là: 2.3 = 6;

⦁ Độ dài trục thực là: 2.6 = 12.

Khi đó tỉ số giữa độ dài trục ảo và độ dài trục thực $\frac{2 b}{2 a} = \frac{6}{12} = \frac{1}{2}$

Vậy ta chọn phương án B.

Câu 9:

Cho điểm A(3; 4) thuộc parabol (P). Phương trình chính tắc của parabol (P) là:

A. $y^{2} = \frac{3}{16} x$

B. $y^{2} = \frac{16}{3} x$

C. $y^{2} = \frac{8}{3} x$

D. $y^{2} = \frac{2}{3} x$

Xem đáp án

Đáp án đúng là: B

Phương trình chính tắc của parabol (P) có dạng: y² = 2px.

Ta có A(3; 4) ∈ (P).

Suy ra 4² = 2.p.3

Do đó 16 = 6p

Khi đó ta có p = 8/3 suy ra 2p = 16/3

Vậy phương trình chính tắc của parabol (P): $y^{2} = \frac{16}{3} x$

Do đó ta chọn phương án B.

Câu 10:

Cho hypebol (H): $\frac{x^{2}}{4} - \frac{y^{2}}{4} = 1$ . Tỉ số giữa tiêu cự và độ dài trục thực bằng:

A. 1;

B. $\frac{\sqrt{2}}{2}$

C. $\frac{\sqrt{2}}{4}$

D. $\sqrt{2}$

Xem đáp án

Đáp án đúng là: D

(H): $\frac{x^{2}}{4} - \frac{y^{2}}{4} = 1$ nên ta có a = b = 2.

Suy ra $c = \sqrt{a^{2} + b^{2}} = \sqrt{4 + 4} = 2 \sqrt{2}$

Khi đó ta có:

⦁ Tiêu cự là: 2c = $2.2 \sqrt{2} = 4 \sqrt{2}$ ;

⦁ Độ dài trục thực là: 2a = 2.2 = 4.

Khi đó $\frac{2 c}{2 a} = \frac{4 \sqrt{2}}{4} = \sqrt{2}$

Vậy ta chọn phương án D.

Câu 11:

Cho điểm M(5; 8) nằm trên parabol (P): $y^{2} = \frac{64}{5} x$ . Độ dài FM bằng:

A. 41/10

B. 41/5

C. 51/5

D. 57/5

Xem đáp án

Đáp án đúng là: B

Ta có $2 p = \frac{64}{5}$

Suy ra $p = \frac{32}{5}$

Do đó $\frac{p}{2} = \frac{16}{5}$

Khi đó ta có tiêu điểm $F (\frac{16}{5}; 0)$

Với $F (\frac{16}{5}; 0)$ và M(5; 8) ta có $\vec{F M} = (\frac{9}{5}; 8)$

Suy ra $F M = \sqrt{{(\frac{9}{5})}^{2} + 8^{2}} = \frac{41}{5}$

Vậy ta chọn phương án B.

Câu 12:

Cho parabol (P) có đường chuẩn là đường thẳng ∆: x + 5 = 0. Điểm M thuộc (P) sao cho khoảng cách từ M đến tiêu điểm của parabol (P) bằng 6. Tọa độ điểm M là:

A. $M (1; 2 \sqrt{5}), M (1; - 2 \sqrt{5})$

B. $M (1; 2 \sqrt{5})$

C. $M (- 1; - 2 \sqrt{5})$

D. $M (- 1; 2 \sqrt{5}), M (- 1; - 2 \sqrt{5})$

Xem đáp án

Đáp án đúng là: A

Phương trình đường chuẩn ∆: x + 5 = 0

Do đó ta có p/2 = 5

Suy ra p = 10.

Từ đó ta thu được phương trình parabol (P): y² = 20x.

Tiêu điểm F của (P) là F(5; 0).

Giả sử điểm M(x_M; y_M) là điểm thuộc (P).

Khi đó $y_{M}^{2} = 20 x_{M}$

Với F(5; 0) và M(x_M; y_M) ta có $\vec{F M} = (x_{M} - 5; y_{M})$

Þ $F M = \sqrt{{(x_{M} - 5)}^{2} + y_{M}^{2}}$

$F M = \sqrt{x_{M}^{2} - 10 x_{M} + 25 + 20 x_{M}} F M = \sqrt{x_{M}^{2} + 10 x_{M} + 25} F M = \sqrt{{(x_{M} + 5)}^{2}} = x_{M} + 5$

Theo đề, ta có FM = 6.

Û x_M + 5 = 6

Û x_M = 1.

Với x_M = 1, ta có $y_{M}^{2} = 20.1 = 20$

Do đó ta chọn phương án A.

Câu 13:

Bác An dự định xây một cái ao hình elip ở giữa khu vườn. Biết trục lớn có độ dài bằng 4 m, độ dài trục nhỏ bằng 2 m. Gọi F₁, F₂ là các tiêu điểm của elip. Khi đó độ dài F₁F₂ bằng:

A. $2 \sqrt{3}$

B. $\sqrt{3}$

C. $\sqrt{5}$

D. $2 \sqrt{5}$

Xem đáp án

Đáp án đúng là: A

Ta có độ dài trục lớn bằng 4 m. Suy ra 2a = 4.

Khi đó a = 2.

Lại có độ dài trục nhỏ bằng 2m. Suy ra 2b = 2.

Khi đó b = 1.

Ta có c² = a² – b² = 2² – 1² = 3.

Suy ra $c = \sqrt{3}$

Vì vậy F₁F₂ = 2c = $2 \sqrt{3}$

Vậy ta chọn phương án A.

Câu 14:

Một tòa tháp có mặt cắt hình hypebol có phương trình $\frac{x^{2}}{36} - \frac{y^{2}}{49} = 1$ . Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp bằng:

A. 43,28 m;

B. 22,25 m;

C. 28,31 m;

D. 57,91 m.

Xem đáp án

Đáp án đúng là: B

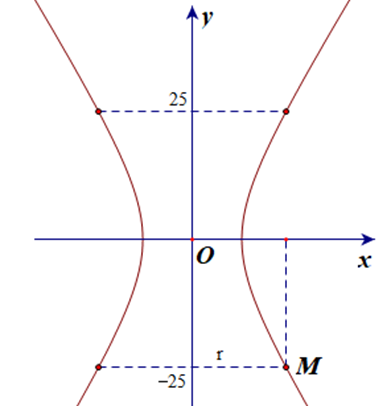
Một tòa tháp có mặt cắt hình hypebol có phương trình x^2/36 - y^2/49 =1 . Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp bằng: (ảnh 1)

Gọi r là bán kính đáy của tháp (r > 0).

Do tính đối xứng của hypebol nên ta có hai bán kính của nóc và đáy tháp đều bằng nhau.

Chọn điểm M(r; –25) nằm trên hypebol.

Ta suy ra $\frac{r^{2}}{36} - \frac{{(- 25)}^{2}}{49} = 1 \Leftrightarrow \frac{r^{2}}{36} = 1 + \frac{{(- 25)}^{2}}{49} = \frac{674}{49} \Leftrightarrow r^{2} = \frac{674}{49} .36 = \frac{24264}{49} S u y r a r = \frac{6 \sqrt{674}}{7} \approx 22, 25$

Vậy bán kính đáy của tháp bằng khoảng 22,25 m.

Do đó ta chọn phương án B.

Câu 15:

Một anten gương đơn hình parabol có phương trình y² = 20x. Ống thu của anten được đặt tại tiêu điểm của nó. Ta sẽ đặt ống thu tại điểm có tọa độ là:

A. (0; 10);

B. (0 ; 5);

C. (10; 0);

D. (5; 0).

Xem đáp án

Đáp án đúng là: D

Phương trình parabol có dạng y² = 2px, với p = 10.

Suy ra $\frac{p}{2} = \frac{10}{2} = 5$

Khi đó tọa độ tiêu điểm F(5; 0).

Vậy ta sẽ đặt ống thu tại điểm có tọa độ (5; 0).

Do đó ta chọn phương án D.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 Bài 4. Ba đường conic trong mặt phẳng tọa độ có đáp án

Trắc nghiệm Toán 10 Bài 4. Ba đường conic trong mặt phẳng tọa độ có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương