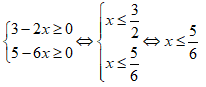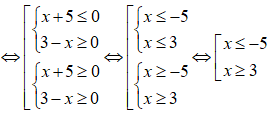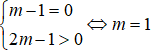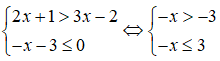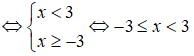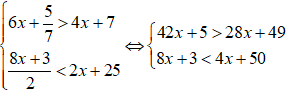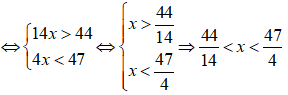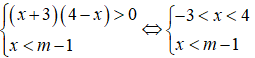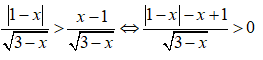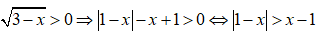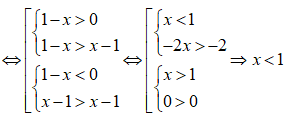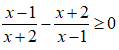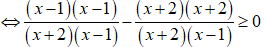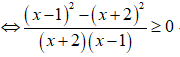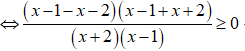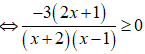Đề kiểm tra 15 phút Đại số 10 Chương 4 có đáp án (Đề 1)
-
1385 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tập xác định của hàm số là
Xem đáp án
Chọn A.
Hàm số xác định khi
Vậy tập xác định của hàm số là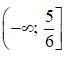 
.
Câu 2:
Cho biểu thức f(x) = (x + 5)(3 - x). Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≤ 0 là
Xem đáp án
Chọn D.
Để f(x) ≤ 0 thì (x + 5)(3 - x) < 0
Vậy x ∈ (-;-5] ∪ [3;+).
Câu 3:
Giá trị của m để bất phương trình x + 3 < mx + 4 có nghiệm là:
Xem đáp án
Chọn A.
x + 3 < mx + 4 ⇔ m(m - 1)x < 1 vô nghiệm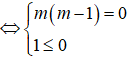 
, vô lí.
Vậy với ∀m ∈ R, bất phương trình có nghiệm.
Câu 4:
Giá trị nào của m thì bất phương trình ( + m + 1)x - 5m ≥ ( + 2)x - 3m - 1 vô nghiệm là:
Xem đáp án
Chọn A.
Bất phương trình ( + m + 1)x - 5m ≥ ( + 2)x - 3m - 1 ⇔ (m - 1)x ≥ 2m - 1 vô nghiệm khi
Câu 5:
Tập nghiệm của hệ bất phương trình là:
Xem đáp án
Chọn B.
Ta có:
Tập nghiệm của hệ bất phương trình là S = [-3;3).
Câu 6:
Số nghiệm nguyên của hệ bất phương trình là:
Xem đáp án
Chọn C.
Ta có:
Mà x nguyên ⇒ x ∈ {4;5;....;11}
Vậy có 8 giá trị của x thỏa mãn hệ bất phương trình.
Câu 7:
Hệ bất phương trình vô nghiệm khi
Xem đáp án
Chọn A.
Hệ bất phương trình vô nghiệm m - 1 ≤ -3 ⇔ m ≤ -2
Câu 8:
Bất phương trình có tập nghiệm là:
Xem đáp án
Chọn D.
Điều kiện: x < 3
Vì 
Vậy tập nghiệm của bất phương trình là S = (-;1)
Câu 9:
Tập nghiệm của bất phương trình là:
Xem đáp án
Chọn D.
Điều kiện: x ≠ -2;1
Khi đó, ta có:
Lập bảng xét dấu.
Tập nghiệm của bất phương trình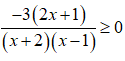 
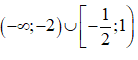
là 
.
Câu 10:
Tìm tất cả các giá trị thực của tham số m để f(x) = m(x - m) - (x - 1) không âm với mọi x ∈ (-; m + 1].
Xem đáp án
Chọn C.
m(x - m) - (x - 1) ≥ 0 ⇔ (m - 1)x ≥ - 1.
+) m = 1 ⇒ x ∈ R. (không thỏa)
+) Xét m > 1 thì (1) ⇔ x ≥ m + 1 không thỏa điều kiện nghiệm đã cho.
+) Xét m < 1 thì (1) ⇔ x ≥ m + 1 thỏa điều kiện nghiệm đã cho.
Vậy m < 1.