Bài tập Cuối chuyên đề 3 có đáp án
-
65 lượt thi
-
8 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
Tìm toạ độ các đỉnh, tiêu điểm và bán kính qua tiêu ứng với điểm M(x; y) của các conic sau:
a) ;
b) ;
c) = 11x.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Elip có => a = 13, b = 12,
Toạ độ các đỉnh của elip là A1(–13; 0), A2(13; 0), B1(0; –12), B2(0; 12).
Toạ độ các tiêu điểm của elip là F1(–5; 0), F2(5; 0).
Các bán kính qua tiêu ứng với điểm M(x; y) là MF1 = a + c/a x = 13 + 5/13 x; MF2 = a – c/a x = 13 – 5/13x.
b) Hypebol có => a = 5, b = 12,
Toạ độ các đỉnh của hypebol là A1(–5; 0), A2(5; 0).
Toạ độ các tiêu điểm của hypebol là F1(–13; 0), F2(13; 0).
Các bán kính qua tiêu ứng với điểm M(x; y) là MF1 = MF2 =
c) Parabol có 2p = 11, suy ra p = 11/2
Toạ độ đỉnh của parabol là O(0; 0).
Toạ độ tiêu điểm của parabol là F
Bán kính qua tiêu ứng với điểm M(x; y) là MF = x + p/2 = x + 11/4
Câu 2:
Cho elip .
a) Xác định toạ độ các đỉnh, tiêu điểm và tìm tâm sai của (E).
b) Viết phương trình chính tắc của parabol (P) có tiêu điểm là tiêu điểm có hoành độ dương của (E).
c) Viết phương trình chính tắc của hypebol (H) có hai đỉnh là hai tiêu điểm của (E), hai tiêu điểm là hai đỉnh của (E). Tìm tâm sai của (H).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Có => a = 5, b = 3,
Toạ độ các đỉnh của elip là A1(–5; 0), A2(5; 0), B1(0; –3), B2(0; 3).
Toạ độ các tiêu điểm của elip là F1(–4; 0), F2(4; 0).
Tâm sai của elip là e = 4/5
b) Gọi phương trình chính tắc của (P) là = 2px (p > 0).
(P) có tiêu điểm là F2(4; 0) => p/2 = 4 => p = 8
=> Phương trình chính tắc của parabol (P) là = 16x.
c) Gọi phương trình chính tắc của (H) là (a > 0, b > 0).
(H) có hai đỉnh là F1(–4; 0), F2(4; 0); hai tiêu điểm là A1(–5; 0), A2(5; 0)
=> a = 4, c = 5 => b =
Vậy phương trình chính tắc của (H) là
Câu 3:
Xác định tâm sai, tiêu điểm và đường chuẩn tương ứng của mỗi đường conic sau:
a) ;
b) ;
c) = 7x.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Đây là một elip.
Có
e =
Suy ra elip có tiêu điểm F1đường chuẩn Δ1: x = -8; tiêu điểm F2(2;0), đường chuẩn Δ1: x = 8 và tâm sai e = 1/2
b) Đây là một hypebol.
Có
e =
Suy ra hypebol có tiêu điểm F1(-4;0_, đường chuẩn Δ1: x = –7/2; tiêu điểm F2(4;0), đường chuẩn Δ1: x = 7/2 và tâm sai e =
c) Đây là một parabol.
CÓ 2p = 7, suy ra p = 7/2
Suy ra parabol có tiêu điểm F(7/4;0) đường chuẩn Δ: x = -7/4 và tâm sai e = 1.Câu 4:
Cho đường thẳng d: x + y – 1 = 0 và điểm F(1; 1). Viết phương trình đường conic nhận F là tiêu điểm, d là đường chuẩn và có tâm sai e trong mỗi trường hợp sau:
a) e = 1/2;
b) e = 1;
c) e = 2.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Gọi M(x; y) là điểm bất kì thuộc conic. Khi đó, ta có:
Vậy phương trình của conic đã cho là
b) Gọi M(x; y) là điểm bất kì thuộc conic. Khi đó, ta có:
Vậy phương trình của conic đã cho là
c) Gọi M(x; y) là điểm bất kì thuộc conic. Khi đó, ta có:
Vậy phương trình của conic đã cho là
Câu 5:
Mặt Trăng chuyển động theo một quỹ đạo là đường elip có tâm sai bằng 0,0549 và nhận tâm Trái Đất là một tiêu điểm. Biết khoảng cách gần nhất giữa tâm Trái Đất và tâm Mặt Trăng là 362600 km. Tính khoảng cách xa nhất giữa tâm Trái Đất và tâm Mặt Trăng.
Nguồn: https://www. universetoday.com

 Xem đáp án
Xem đáp án
Hướng dẫn giải
Chọn hệ trục toạ độ sao cho tâm Trái Đất trùng với tiêu điểm F1 của elip và trục Ox đi qua hai tiêu điểm của elip, đơn vị trên các trục toạ độ là kilômét.
Khi đó phương trình của elip có dạng (a > b > 0).
Gọi toạ độ của Mặt Trăng là M(x; y) thì khoảng cách giữa tâm Trái Đất và tâm Mặt Trăng là MF1 = a – ex ≥ a – ea (vì x ≤ a). Do đó khoảng cách gần nhất giữa tâm Trái Đất và tâm Mặt Trăng là a – ea, suy ra a – ea = 362600 =>a =
Mặt khác vì x ≥ –a nên a – ex ≤ a + ea nên khoảng cách xa nhất giữa tâm Trái Đất và tâm Mặt Trăng là a + ea = a(1 + e) = 404726 (km).
Vậy khoảng cách xa nhất giữa tâm Trái Đất và tâm Mặt Trăng là 404726 km.
Câu 6:
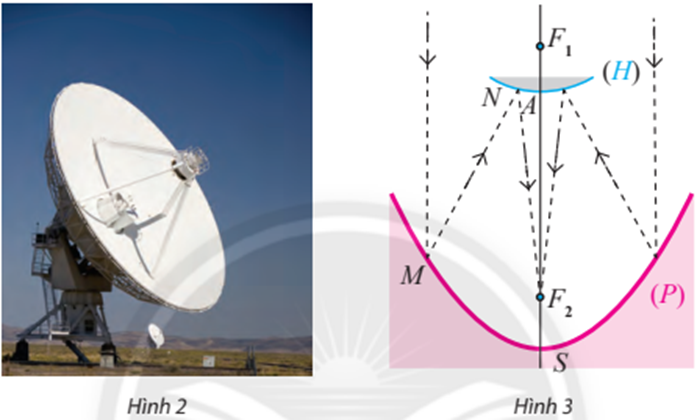
Ta đã biết tính chất quang học của ba đường conic (xem phần đọc thêm Bạn có biết? ở trang 72, sách giáo khoa Toán 10, tập hai). Hypebol cũng có tính chất quang học tương tự như elip: Tia sáng hướng tới tiêu điểm F1 của hypebol (H) khi gặp một nhánh của (H) sẽ cho tia phản xạ đi qua F2. Một nhà nghiên cứu thiết kế một kính thiên văn vô tuyến chứa hai gương có mặt cắt hình parabol (P) và hình một nhánh của hypebol (H). Parabol (P) có tiêu điểm F1 và đỉnh S. Hypebol (H) có đỉnh A, có chung một tiêu điểm là F1 với (P) và còn có tiêu điểm thứ hai F2 (Hình 3).
Nguyên tắc hoạt động của kính thiên văn đó như sau: Tín hiệu đến từ vũ trụ được xem như song song với trục của parabol (P), khi đến điểm M của (P) sẽ cho tia phản xạ theo hướng MF1, tia này gặp (H) tại điểm N và cho tia phản xạ tới F2 là nơi thu tín hiệu. Cho biết SF1 = 14 m, SF2 = 2 m và AF1 = 1 m. Hãy viết phương trình chính tắc của (P) và (H).
(Nguồn: https://sciencestruck.com/parabolic – mirror – working – principle – applications)
 Xem đáp án
Xem đáp án
Hướng dẫn giải
+) Gọi phương trình chính tắc của (H) là (a > 0, b > 0).
F1, F2 là hai tiêu điểm của (H) nên 2c = F1F2 = SF1 – SF2 = 14 – 2 = 12, suy ra c = 6.
AF2 = F1F2 – AF1 = 12 – 1 = 11.
Vì A thuộc (H) nên 2a = |AF1 – AF2| = |1 – 11| = 10, suy ra a = 5,
Vậy phương trình chính tắc của (H) là
+) Gọi phương trình chính tắc của (P) là = 2px (p > 0).
S là đỉnh và F1 là tiêu điểm của parabol nên p/2 = SF1 = 14, suy ra p = 28.
Vậy phương trình chính tắc của (P) là = 56x.
Câu 7:
Mặt cắt của một chảo ăng-ten là một phần của parabol (P). Cho biết đầu thu tín hiệu đặt tại tiêu điểm F cách đỉnh O của chảo một khoảng là 1/6 m.

a) Viết phương trình chính tắc của (P).
b) Tính khoảng cách từ một điểm M(0,06; 0,2) trên ăng-ten đến F.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Gọi phương trình chính tắc của parabol là = 2px (p > 0).
Ta có p/2 = OF = 1/6 p = 1/3
=> phương trình chính tắc của parabol là = 2/3 x
b) Theo công thức bán kính qua tiêu ta có:
MF = x + p/2 = 0,06 + 1/6 = 59/150 (m).
Vậy khoảng cách từ điểm M(0,06; 0,2) trên ăng-ten đến F là 59/150 mét.Câu 8:
Gương phản chiếu của một đèn chiếu có mặt cắt hình parabol (Hình 5). Chiều rộng giữa hai mép vành của gương là MN = 32 cm và chiều sâu của gương là OH = 24 cm.
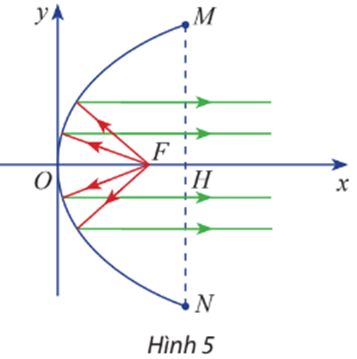
a) Viết phương trình chính tắc của parabol đó.
b) Biết bóng đèn đặt tại tiêu điểm F của gương. Tính khoảng cách từ bóng đèn tới đỉnh O của gương.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Gọi phương trình chính tắc của parabol là = 2px (p > 0).
Dựa vào hình vẽ, ta có: khi x = 24 thì y = 16
Vậy phương trình chính tắc của parabol là = 32/3 x
b) Khoảng cách từ bóng đèn tới đỉnh O của gương là OF = p/2 = 8/3 (cm).