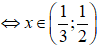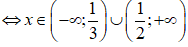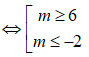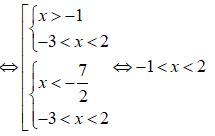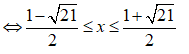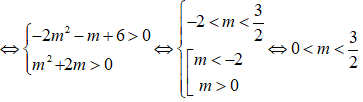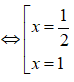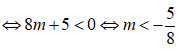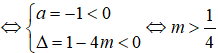10 câu hỏi trắc nghiệm thuộc Đề kiểm tra 15 phút Đại số 10 Chương 4 có đáp án (Đề 2)

Đề kiểm tra 15 phút Đại số 10 Chương 4 có đáp án (Đề 1)

Đề kiểm tra 15 phút Đại số 10 Chương 4 có đáp án (Đề 2)

1417 lượt thi
10 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Dấu của tam thức 3 $x^{2}$ - 2x + 1 là:

A. 3 $x^{2}$ - 2x + 1 ≥ 0, ∀x ∈ R

B. 3 $x^{2}$ - 2x + 1 > 0,∀x ∈ R

C. 3 $x^{2}$ - 2x + 1 < 0, ∀x ∈ R

D. 3 $x^{2}$ - 2x + 1 ≤ 0,∀x ∈ R

Xem đáp án

Chọn B.

Ta có Δ' = -2 < 0, a = 3 > 0 ⇒ Tam thức 3 $x^{2}$ - 2x + 1 có cùng dấu với hệ số a ⇒ 3x2 - 2x + 1 > 0, ∀x ∈ R

Câu 2:

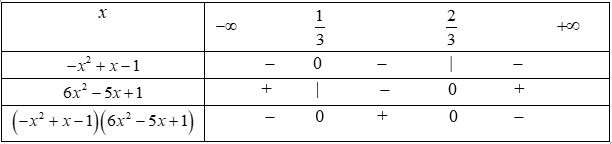
Cho biểu thức: (- $x^{2}$ + x - 1)(6 $x^{2}$ - 5x + 1)

A. (- $x^{2}$ + x - 1)(6 $x^{2}$ - 5x + 1) > 0 $\Leftrightarrow x \in (\frac{1}{3}; \frac{1}{2})$

B. (- $x^{2}$ + x - 1)(6 $x^{2}$ - 5x + 1) < 0 $\Leftrightarrow x \in (\frac{1}{3}; \frac{1}{2})$

C. (- $x^{2}$ + x - 1)(6 $x^{2}$ - 5x + 1) > 0 $\Leftrightarrow x \in (- \infty; \frac{1}{3}) \cup (\frac{1}{2}; + \infty)$

D. (- $x^{2}$ + x - 1)(6 $x^{2}$ - 5x + 1) < 0 $\Leftrightarrow x \in (- \infty; \frac{1}{3})$

Xem đáp án

Chọn A.

Ta có:

+) - $x^{2}$ + x - 1 = 0: PT vô nghiệm

+) 6 $x^{2}$ - 5x + 1 = 0

Lập bảng xét dấu:

Suy ra

(- $x^{2}$ + x - 1)(6 $x^{2}$ - 5x + 1) > 0

(- $x^{2}$ + x - 1)(6 $x^{2}$ - 5x + 1) < 0

Câu 3:

Tập nghiệm của bất phương trình $x^{2}$ + x - 12 < 0 là:

A. S = (-4;3)

B. S = (- $\infty$ ;-4)

C. S = (3;+ $\infty$ )

D. S = R

Xem đáp án

Chọn A.

Tam thức f(x) = $x^{2}$ + x - 12 có a = 1 > 0 và có hai nghiệm $x_{1}$ = -4; $x_{2}$ = 3

(f(x) trái dấu với hệ số a).

Suy ra $x^{2}$ + x - 12 < 0 ⇔ -4 < x < 3

Vậy tập nghiệm của bất phương trình là S = (-4;3).

Câu 4:

Giá trị của tham số m để phương trình $x^{2}$ - mx + m + 3 = 0 có nghiệm là:

A. m $\infty$ (- $\infty$ ;-2]

B. m $\infty$ [6;+ $\infty$ )

C. m $\infty$ [-2;6]

D. m $\infty$ (- $\infty$ ;-2] ∪ [6;+ $\infty$ )

Xem đáp án

Chọn D.

Phương trình có nghiệm khi và chỉ khi Δ ≥ 0

⇔ $m^{2}$ - 4(m + 3) ≥ 0

⇔ $m^{2}$ - 4m - 12 ≥ 0

Vậy với m ∈ (- $\infty$ ;-2] ∪ [6;+ $\infty$ ) thì phương trình có nghiệm

Câu 5:

Tập nghiệm của hệ bất phương trình $\{\begin{cases} 2 x^{2} + 9 x + 7 > 0 \\ x^{2} + x - 6 < 0 \end{cases}$ là:

A. S = [-1;2]

B. S = (-1;2)

C. S = (- $\infty$ ;-1)

D. S = R

Xem đáp án

Chọn B.

Ta có:

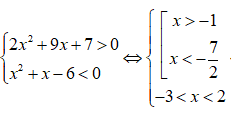
Vậy tập nghiệm hệ bất phương trình là S = (-1;2).

Câu 6:

Cho hệ bất phương trình $\{\begin{cases} m x^{2} - x - 5 \leq 0 \\ (1 - m) x^{2} + 2 m x + m + 2 \geq 0 \end{cases}$ . Các giá trị của x thỏa mãn hệ bất phương trình khi m = 1 là:

A. $S = [\frac{1 - 2 \sqrt{21}}{2}; \frac{1 + 2 \sqrt{21}}{2}]$

B. $S = [\frac{1 - 3 \sqrt{21}}{2}; \frac{1 + 3 \sqrt{21}}{2}]$

C. $S = [\frac{1 - 4 \sqrt{21}}{2}; \frac{1 + 4 \sqrt{21}}{2}]$

D. $S = [\frac{1 - \sqrt{21}}{2}; \frac{1 + \sqrt{21}}{2}]$

Xem đáp án

Chọn D.

Với m = 1 hệ bất phương trình trở thành:

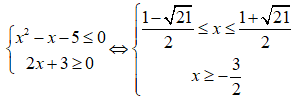
Vậy tập nghiệm hệ bất phương trình là

Câu 7:

Giá trị của m để bất phương trình $m^{2}$ x + m(x + 1) - 2(x - 1) > 0 nghiệm đúng với mọi x ∈ [-2;1] là:

A. 0 < m < $\frac{3}{2}$

B. 0 < m

C. m < $\frac{3}{2}$

D. $[\begin{matrix} m < 0 \\ m > \frac{3}{2} \end{matrix}$

Xem đáp án

Chọn A.

Bất phương trình $m^{2}$ x + m(x + 1) - 2(x - 1) > 0 có nghiệm đúng với mọi x ∈ [-2;1] khi và chỉ khi

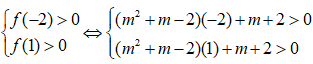
Câu 8:

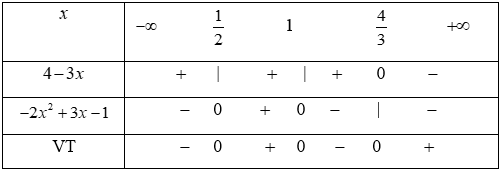
Tập nghiệm của bất phương trình (4 - 3x)(-2 $x^{2}$ + 3x - 1) ≤ 0 là:

A. T = (- $\infty$ ; $\frac{1}{2}$ ]

B. T = [1; $\frac{4}{3}$ ]

C. T = (- $\infty$ ; $\frac{1}{2}$ ] $\cup$ [1; $\frac{4}{3}$ ]

D. T = ( $\frac{1}{2}$ ;1)

Xem đáp án

Chọn C.

Ta có :

+) 4 - 3x = 0 ⇔ x = 4/3

+) -2 $x^{2}$ + 3x - 1 = 0

Lập bảng xét dấu :

Vậy tập nghiệm của bất phương trình (4 - 3x)(-2 $x^{2}$ + 3x - 1) ≤ 0 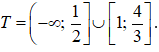là

Câu 9:

Giá trị của m để biểu thức $\frac{- x^{2} + 4 (m + 1) x + 1 - 4 m^{2}}{- 4 x^{2} + 5 x - 2}$ luôn dương là:

A. m < $- \frac{5}{8}$

B. m > $- \frac{5}{8}$

C. m $\leq$ $- \frac{5}{8}$

D. m $\geq$ $- \frac{5}{8}$

Xem đáp án

Chọn A.

Tam thức -4 $x^{2}$ + 5x - 2 có a = -4 <0, Δ = -7 < 0 suy ra -4 $x^{2}$ + 5x - 2 < 0, ∀x

Do đó

luôn dương khi và chỉ khi - $x^{2}$ + 4(m + 1)x + 1 - 4 $m^{2}$ luôn âm

Vậy với 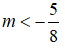thì biểu thức luôn dương.

Câu 10:

Giá trị của m để biểu thức - $x^{2}$ - 2x - m luôn âm là:

A. $- \frac{1}{4}$ < m

B. m < 0

C. $- \frac{1}{4}$ < m < 0

D. m > $\frac{1}{4}$

Xem đáp án

Chọn D.

Biểu thức - $x^{2}$ - 2x - m < 0 (∀x ∈ R)

Vậy với thì biểu thức - $x^{2}$ - 2x - m luôn âm.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra 15 phút Đại số 10 Chương 4 có đáp án (Đề 1)

Đề kiểm tra 15 phút Đại số 10 Chương 4 có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương