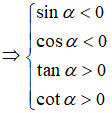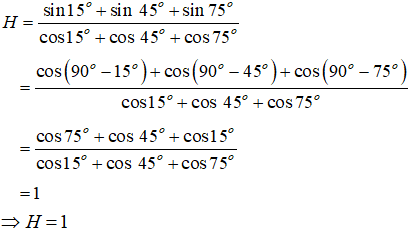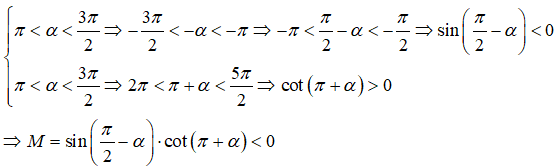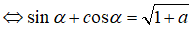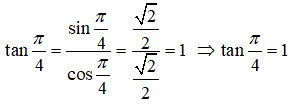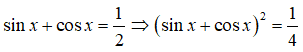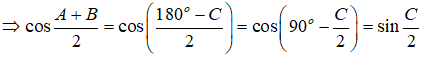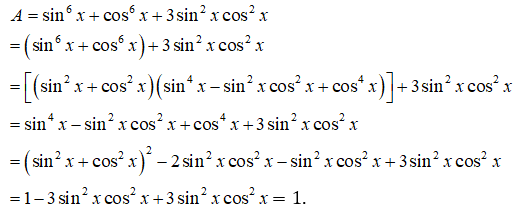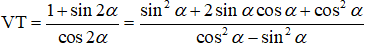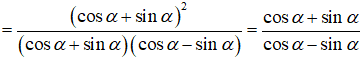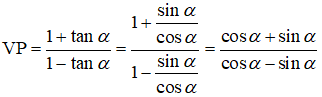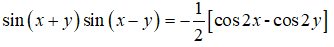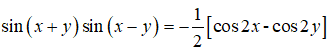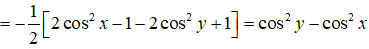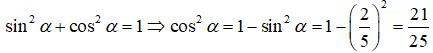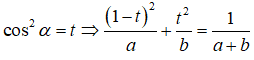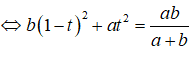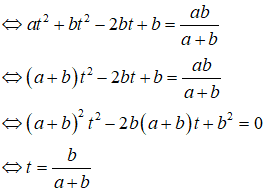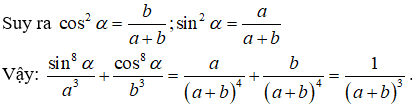15 câu hỏi trắc nghiệm thuộc Đề kiểm tra 45 phút Đại số 10 Chương 6 có đáp án (Đề 2)

Đề kiểm tra 45 phút Đại số 10 Chương 6 có đáp án (Đề 1)

Đề kiểm tra 45 phút Đại số 10 Chương 6 có đáp án (Đề 2)

1199 lượt thi
15 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Phần I: Trắc nghiệm

Điểm cuối của α thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là không đúng ?

A. sin⁡α > 0

B. cos⁡α < 0

C. tan⁡α > 0

D. cot⁡α > 0

Xem đáp án

Chọn A.

Điểm cuối của α thuộc góc phần tư thứ ba của đường tròn lượng giác

Câu 2:

Cho $0 < α < \frac{π}{2}$ . Trong các khẳng định sau, khẳng định nào đúng?

A. sin⁡(α - π) ≥ 0

B. sin⁡(α - π) ≤ 0

C. sin⁡(α - π) < 0

D. sin⁡(α - π) < 0

Xem đáp án

Chọn C.

Ta có:

Câu 3:

Giá trị của biểu thức sau là:

$H = \frac{\sin 15 ° + \sin 45 ° + \sin 75 °}{\cos 15 ° + \cos 45 ° + \cos 75 °}$

A. H = 1

B. H = -1

C. H = 0

D. H = 1/2

Xem đáp án

Chọn A.

Ta có:

Câu 4:

Cho $π < α < \frac{3 π}{2}$ .

Dấu của biểu thức $M = \sin (\frac{π}{2} - α) . c o t (π + α)$ là:

A. M ≥ 0

B. M > 0

C. M ≤ 0

D. M < 0

Xem đáp án

Chọn D.

Ta có:

Câu 5:

Cho sin⁡2α = a với 0 < α < 90o. Giá trị của sin⁡α + cos⁡α bằng:

A. $(\sqrt{2} - 1) a + 1$

B. $\sqrt{a + 1} - \sqrt{a^{2} - a}$

C. $(\sqrt{2} - 1) a + 1$

D. $\sqrt{a + 1}$

Xem đáp án

Chọn D.

Ta có: sin⁡2α = a ⇒ 2sin⁡α.cos⁡α = a với 0 < α < 90o.

$\sin^{2} α$ + $\cos^{2} α$ = 1

⇔ $\sin^{2} α$ + $\cos^{2} α$ + 2sin⁡αcos⁡α - 2sin⁡αcos⁡α = 1

⇔ (sin⁡α + cosα $)^{2}$ - 2sin⁡αcos⁡α = 1

⇔ (sin⁡α + cosα $)^{2}$ = 1 + 2sin⁡αcos⁡α

⇔ (sin⁡α + cosα $)^{2}$ = 1 + a

Câu 6:

Cho sin⁡α = 0,6 với $\frac{π}{2} < α < π$ . Giá trị của cos2α bằng:

A. 0,96

B. -0,96

C. 0,28

D. -0,28

Xem đáp án

Chọn C.

Áp dụng công thức: cos2α = 1 - 2 $\sin^{2} α$ = 1 - 2.(0,6 $)^{2}$ = 0,28

Câu 7:

Giá trị của tan⁡(π/4) là

A. 1

B. $\frac{\sqrt{2}}{2}$

C. $- \frac{\sqrt{2}}{2}$

D. -1

Xem đáp án

Chọn A.

Câu 8:

Số đo radian của góc 225 $°$ là:

A. $\frac{3 π}{4}$

B. $\frac{5 π}{4}$

C. $\frac{7 π}{4}$

D. $\frac{π}{4}$

Xem đáp án

Chọn B.

Số đo radian của góc 225 $°$ là:

Câu 9:

Nếu sin⁡x + cos⁡ x = 1/2 thì 3sin⁡x + 2cos⁡x bằng

A. hay $\frac{5 + \sqrt{7}}{4}$

B. $\frac{5 - \sqrt{5}}{7}$ hay $\frac{5 + \sqrt{5}}{4}$

C. $\frac{2 - \sqrt{3}}{5}$ hay $\frac{2 + \sqrt{3}}{5}$

D. $\frac{3 - \sqrt{2}}{5}$ hay $\frac{3 + \sqrt{2}}{5}$

Xem đáp án

Chọn A.

Ta có:

Câu 10:

Trong tam giác ABC, đẳng thức nào dưới đây luôn đúng?

A. cos A = sin B

B. tan A = cot (B + $\frac{π}{2}$ )

C. cos $\frac{A + B}{2}$ = sin $\frac{C}{2}$

D. sin (A + B) = cos C

Xem đáp án

Chọn C.

Xét tam giác ABC, ta có: ∠A + ∠B + ∠C = 180 $°$ ⇒ ∠A + ∠B = 180 $°$ - ∠C

Câu 11:

Chọn đẳng thức đúng:

A. sin⁡(π - α) = sin⁡α

B. cos⁡(π - α) = cos⁡α

C. tan⁡(π - α) = tan⁡α

D. cot⁡(π - α) = cot⁡α

Xem đáp án

Chọn A.

Ta có: sin⁡(π - α) = sin⁡α; cos⁡(π - α) = -cos⁡α; tan⁡(π - α) = -tan⁡α; cot⁡(π - α) = -cot⁡α

Câu 12:

Giá trị của biểu thức A = $\sin^{6} x$ + $\cos^{6} x$ + 3 $\sin^{2} c o s^{2}$ là :

A. A = -1

B. A = 1

C. A = 4

D. A = -4

Xem đáp án

Chọn B.

Câu 13:

Phần II: Tự luận

Chứng minh đẳng thức (khi các biểu thức có nghĩa):

1) $\frac{1 + \sin 2 α}{\cos 2 α} = \frac{1 + \tan α}{1 - \tan α}$

2) $\sin (x + y) \sin (x - y) = \cos^{2} y - \cos^{2} x$

Xem đáp án

1) Xét vế trái:

Ta thấy VT = VP ⇒ ĐCCM

2) Ta có:

Câu 14:

Cho $\sin α = \frac{2}{5} (\frac{π}{2} < α < π)$ . Tính các giá trị cos⁡α, tan⁡α, cot⁡α.

Xem đáp án

Ta có:

Mà

Câu 15:

Biết $\frac{\sin^{4} α}{a} + \frac{\cos^{4} α}{b} = \frac{1}{a + b}$

Tính giá trị biểu thức $A = \frac{\sin^{8} x}{a^{3}} + \frac{\cos^{8} α}{b^{3}}$

Xem đáp án

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra 45 phút Đại số 10 Chương 6 có đáp án (Đề 1)

Đề kiểm tra 45 phút Đại số 10 Chương 6 có đáp án (Đề 2)

Danh sách câu hỏi

Phần I: Trắc nghiệm

Phần II: Tự luận

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương