Đề thi Học kì 1 Toán 10 Chân trời sáng tạo có đáp án- Đề 1
-
973 lượt thi
-
39 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho định lý “Hai góc đối đỉnh thì bằng nhau”. Mệnh đề nào sau đây đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Từ định lý “Hai góc đối đỉnh thì bằng nhau”, ta có thể phát biểu lại định lí này như sau:
Hai góc đối đỉnh là điều kiện đủ để hai góc đó bằng nhau. Do đó D đúng và B sai.
Hai góc bằng nhau là điều kiện cần để hai góc đó đối đỉnh. Do đó C sai.
Vì hai góc bằng nhau nhưng chưa chắc đối đỉnh do đó đáp án A là sai.
Câu 2:
Cho tập hợp A = {x ∈ ℝ| – 1 ≤ x < 3}. Xác định phần bù của tập hợp A trong ℝ.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có: A = {x ∈ ℝ| – 1 ≤ x < 3} = [ – 1; 3)
Khi đó ℝ \ A = ℝ \ [ – 1; 3) = (– ∞; – 1) ∪ [3; + ∞).
Câu 3:
Hệ nào dưới đây là hệ bất phương trình bậc nhất hai ẩn?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Hệ bất phương trình bậc nhất hai ẩn là hệ gồm các bất phương trình bậc nhất hai ẩn. Do đó đáp án B là đúng.
Câu 4:
Một bệnh viện thống kê số ca nhập viện do tai nạn giao thông mỗi ngày trong tháng 9/2020 ở bảng sau:
|
Số ca |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
12 |
15 |
|
Số ngày |
2 |
3 |
4 |
6 |
3 |
2 |
2 |
3 |
2 |
1 |
1 |
1 |
Khoảng tứ phân vị của dãy số liệu trên là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Dãy số liệu trên có 30 số liệu.
Số trung vị của dãy số liệu là số trung bình cộng của số liệu ở vị trí thứ 15 và 16: Q2 = .
Số trung vị của nửa số liệu bên trái là: Q1 = 2.
Số trung vị của nửa số liệu bên phải là: Q2 = 7.
Khoảng tứ phân vị ∆Q = Q2 – Q1 = 7 – 2 = 5.
Câu 5:
Cho hàm số y = x2 – 2x – 2 có đồ thị là parabol (P) và đường thẳng (d) có phương trình y = x + m. Giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B sao cho OA2 + OB2 đạt giá trị nhỏ nhất là:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Xét phương trình hoành độ giao điểm:
x2 – 2x – 2 = x + m (1)
⇔ x2 – 3x – 2 – m = 0
Ta có: ∆ = (– 3)2 – 4.1.(– 2 – m) = 17 + 4m
Để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt A, B thì phương trình (1) có hai nghiệm phân biệt ⇔ ∆ = 17 + 4m > 0 ⇔ m > .
Gọi x1 và x2 là nghiệm của phương trình (1).
Áp dụng định lí Vi – et ta được: .
Đặt A(x1; y1) và B(x2; y2)
⇒ OA = ⇒ OA2 =
⇒ OB = ⇒ OB2 = .
⇒ OA2 + OB2 =
=
=
=
= 2m2 + 10m + 26
= 2(m + )2 + ≥
Vậy OA2 + OB2 đạt giá trị nhỏ nhất bằng khi m = .
Câu 6:
Hà ghi lại số liệu từ trang web của Tổng cục thống kê bảng dân số Việt Nam qua các năm từ 2015 đến 2020:
|
Năm |
Số dân |
|
2015 |
92 677 076 |
|
2016 |
93 640, 422 |
|
2017 |
94 600 648 |
|
2018 |
95 545 962 |
|
2019 |
96 462 106 |
|
2020 |
97 338 579 |
Bạn Hà đã ghi nhầm dân số của năm nào?
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Dân số Việt Nam năm 2016 là 93 640 422 (người). Do đó bạn Hà ghi sai số liệu năm 2016.
Câu 7:
Hàm số nào dưới đây là hàm số không chẵn cũng không lẻ?
A. y = – 2|x – 1|;
B. y = x3 – 5x;
D. y = – x.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Tập xác định của các hàm số đã cho là D = ℝ
Lấy x ∈ D khi đó – x ∈ D, ta có:
+) y(– x) = – 2|(– x) – 1| = – 2|x + 1| ≠ y(x).
Do đó hàm số không chẵn cũng không lẻ.
+) y(– x) = (– x)3 – 5(– x) = - x3 + 5x = - (x3 – 5x) = – y(x).
Do đó hàm số là hàm số lẻ.
+) .
Do đó hàm số là hàm số chẵn.
+) y(– x) = – (– x) = x = – y(x).
Do đó hàm số là hàm lẻ.
Câu 8:
Trong các hàm số sau, đồ thị của hàm số nhận đường thẳng x = 1 làm trục đối xứng là
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có:
Hàm số bậc hai y = – 2x2 + 4x + 1 có a = – 2, b = 4, c = 1. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = 2x2 + 4x + 3 có a = 2, b = 4, c = 3. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = 2x2 – 2x + 1 có a = 2, b = – 2, c = 1. Khi đó trục đối xứng là x = .
Hàm số bậc hai y = x2 – x + 5 có a = 1, b = –1, c = 5. Khi đó trục đối xứng là x = .
Câu 9:
Tập xác định D của hàm số là
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Hàm số xác định khi và chỉ khi .
Do đó tập xác định của hàm số là: D = [– 2; 2] \ {0}.
Vậy đáp án đúng là A.
Câu 10:
Cho hàm số y = (m – 2021)x + m – 2. Điều kiện để hàm số đồng biến trên ℝ là
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Để hàm số y = (m – 2021)x + m – 2 đồng biến trên ℝ khi m – 2021 > 0 ⇔ m > 2021.
Vậy với m > 2021 thì hàm số đồng biến trên ℝ.
Câu 11:
Cho , với 0° < α < 90°. Giá trị của cosα bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Ta có: tan2α + 1 =
⇔ cos2α =
⇔ cos2α =
⇔ cosα = (0° < α < 90°).
Vậy chọn đáp án C
Câu 12:
Tính giá trị biểu thức sau: sin12° + sin178° + cos106° + cos74°
 Xem đáp án
Xem đáp án
Đáp án đúng là A
sin12° + sin178° + cos106° + cos74°
= sin12° + sin(180° – 12°) + cos(180° – 74°) + cos74°
= sin12° + sin12° – cos74° + cos74°
= 2.sin12°.
Câu 13:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Xét tam giác ABC, có: (định lí tổng ba góc trong tam giác)
Áp dụng định lí sin trong tam giác ABC, ta được:
.
Câu 14:
Cho bảng biến thiên sau:
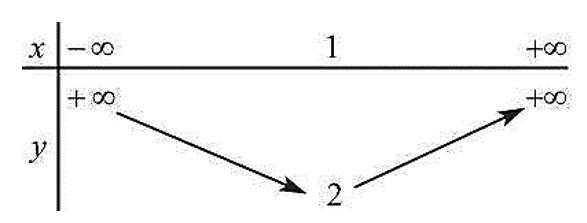
Đồ thị hàm số bậc hai tương ứng với bảng biến thiên trên là :
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Gọi hàm số bậc hai cần tìm là: y = ax2 + bx + c (với a, b, c ∈ ℝ, a ≠ 0)
Dựa vào bảng biến thiên ta thấy a > 0 nên đáp án D sai.
Ta có: xI = ⇔ b = – 2a. Do đó A sai.
Ta lại có: yI = ⇔ ∆ = – 8a ⇔ b2 – 4ac = – 8a ⇔ 4a2 – 4ac = – 8a ⇔ a – c = – 2 ⇔ c = a + 2
+) Nếu a = 1 thì b = – 2 và c = 3. Do đó B sai.
+) Nếu a = 2 thì b = – 4 và c = 4. Do đó C đúng.
Câu 15:
Phát biểu nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Hai vectơ cùng phương thì có thể cùng hướng hoặc ngược hướng. Do đó D là phát biểu sai.
Câu 16:
Cho hình vuông ABCD. Hãy chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có: là hai vectơ không cùng phương dù chúng có cùng độ dài. Suy ra . Do đó A sai.
Ta có: (quy tắc hình bình hành). Do đó B đúng.
Nếu độ dài cạnh của hình vuông là a thì = a và . Suy ra . Do đó C sai.
Hai vectơ và cùng phương cùng độ dài nhưng ngược hướng. Suy ra . Do đó D sai.
Câu 17:
Cho hình vẽ sau:
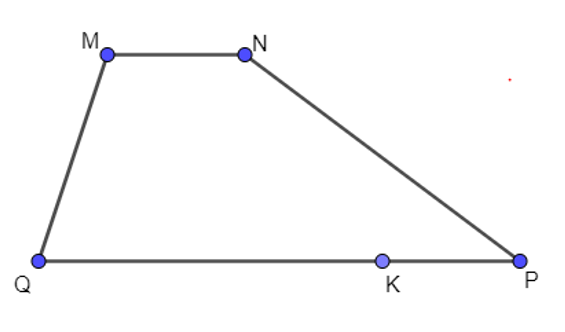
Trong các vectơ trên hình, có bao nhiêu vectơ cùng phương với vectơ ?
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Hai vec tơ cùng phương là hai vectơ có giá song song hoặc trùng nhau. Khi đó các vectơ cùng phương với vectơ là .
Vậy có tất cả 7 vectơ cùng phương với vectơ .
Câu 18:
Để lắp đường dây cao thế từ vị trí A đến vị trí B phải tránh một ngọn núi, do đó người ta phải nối thẳng đường dây từ vị trí A đến vị trí C dài 9 km, rồi nối từ vị trí C đến B dài 12km. Biết góc tạo bởi 2 đoạn dây AC và CB là 52°. Hỏi so với việc nối thẳng từ A đến B phải tốn thêm bao nhiêu mét dây?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Áp dụng định lí cos vào tam giác ABC ta được:
AB2 = AC2 + CB2 – 2.AC.CB.cos52°
= 92 + 122 – 2.9.12.cos52°
≈ 92,0
⇔ AB ≈ 9,6 m.
So với việc nối thẳng từ A đến B phải tốn thêm số mét dây là: 9 + 12 – 9,6 ≈ 11,4 (m).
Câu 19:
Cho hình chữ nhật ABCD tâm O. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC. Chọn khẳng định đúng trong các khẳng định sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
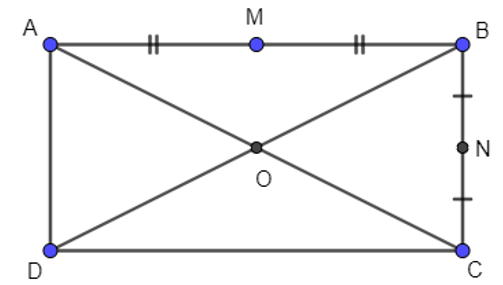
+) Ta có: và là hai vectơ cùng phương cùng độ dài nhưng ngược hướng. Do đó . Suy ra A sai.
+) Xét tam giác ABC, có:
O là trung điểm của AC
N là trung điểm của BC
Suy ra ON là đường trung bình của tam giác ABC
Khi đó ON // AB và ON = AB = AM = MB.
Do đó . Suy ra B đúng.
+) Ta có: và là hai vectơ có cùng độ dài nhưng không cùng hướng. Do đó . Suy ra C sai.
+) Ta có: và là hai vectơ không cùng độ dài và không cùng hướng. Do đó . Suy ra D sai.
Câu 21:
Cho tam giác đều ABC nội tiếp đường tròn tâm O, bán kính bằng 1. Gọi M là điểm nằm trên đường tròn (O), độ dài vectơ bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Vì ABC là tam giác đều nên O là trọng tâm tam giác ABC. Khi đó
Ta có:
Ta lại có: M là điểm nằm trên đường tròn nên MO = 1.
.
Câu 22:
Cho = 12,096384. Số gần đúng của với độ chính xác d = 0,0004 là:
A. 12,096;
B. 12,09638;
C. 12,0964;
D. 12,10.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Hàng của chữ số khác 0 đầu tiên của độ chính xác là hàng phần chục nghìn. Quy tròn số đến hàng phần chục nghìn ta được số gần đúng của là: 12,0964.
Câu 23:
Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và CD. Đặt , . Hãy phân tích vectơ theo 2 vectơ và :.
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Ta có:
⇔
⇔
⇔
⇔.
Câu 24:
Cho số gần đúng là a = 1,2357 với độ chính xác là d = 0,01. Số quy tròn của số a là:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Hàng lớn nhất của độ chính xác là hàng phần trăm thì ta cần làm tròn đến hàng phần mười. Khi đó ta có số quy tròn của số gần đúng a là 1,2.
Câu 25:
Cho hình thoi ABCD có cạnh bằng 4. . Tính :
A. 8;
B. 16;
C. 24;
D. 32.
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Ta có hình vẽ sau:
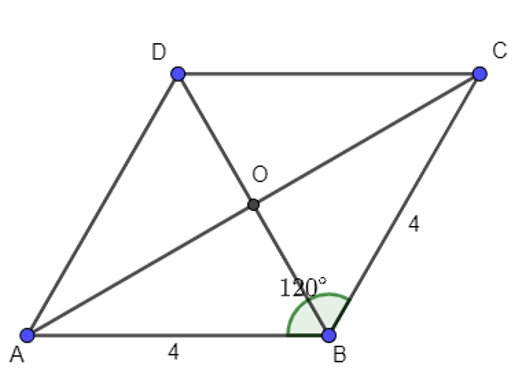
Vì ABCD là hình thoi nên AC ⊥ BD tại O
⇒ (tính chất hình thoi)
Xét tam giác ABC vuông tại O, có:
AO = sin.AB = sin60°.4 = .
⇒ AC = 2.AO = 2.= .
Ta có:
Khi đó: .
Câu 26:
Cho hình thang vuông ABCD có . Tính :
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Vì ABCD là hình thang vuông tại A và D nên AB ⊥ AD. Do đó = 0.
Câu 27:
Cho mẩu tin sau:
Trong tháng 01/2021 có 47 dự án được cấp phép mới với số vốn đăng kí đạt gần 1,3 tỉ USD, giảm khoảng 81,8% về số dự án và 70,3% về số vốn đăng kí so với cùng kì năm trước; 46 lượt dự án đã cấp phép từ các năm trước đăng kí điều chỉnh vốn đầu tư với số vốn tăng thêm trên 0,5 tỉ USD, tăng gần 41,4%.
Trong các số liệu đã cho trong bài, số số gần đúng là:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Trong các số liệu đã cho trong bài, ta có:
- Các số đúng là: 47; 46.
- Các số gần đúng là: 1,3; 81,8%; 70,3%; 0,5; 41,4%.
Vậy có 5 số số gần đúng.
Câu 28:
Cho tam giác ABC đều có cạnh bằng a, gọi H là trung điểm của cạnh BC. Độ dài của vectơ bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Ta có:
Khi đó .
Câu 29:
: Lớp 10A có 40 học sinh. Tỉ lệ số lượng mỗi loại học lực của học sinh lớp 10A được biểu diễn bằng biểu đồ sau:
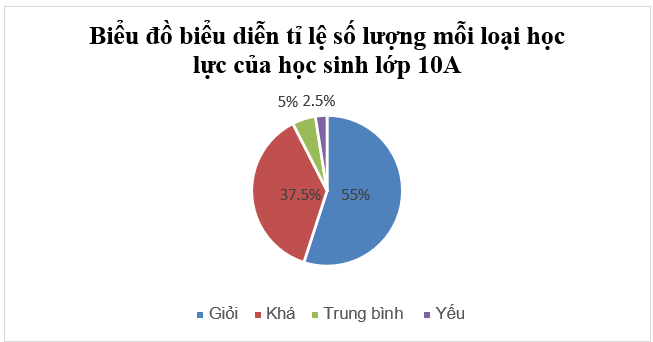
Hỏi số lượng học sinh khá của lớp 10A là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Tỉ lệ học sinh khá trong lớp 10A là 37,5% nên số học sinh đạt học lực khá của lớp 10A là:
37,5%.40 = 15 (học sinh)
Vậy lớp 10A có 15 học sinh đạt học lực khá.
Câu 30:
Một xạ thủ bắn súng 10 lần liên tiếp, số điểm của xạ thủ đạt được được ghi lại trong bảng sau:
|
Số lần |
Lần 1 |
Lần 2 |
Lần 3 |
Lần 4 |
Lần 5 |
Lần 6 |
Lần 7 |
Lần 8 |
Lần 9 |
Lần 10 |
|
Số điểm |
8 |
6 |
7 |
6 |
9 |
8 |
10 |
7 |
7 |
8 |
Số trung vị của số liệu trên là:
 Xem đáp án
Xem đáp án
Đáp án đúng là D
Sắp xếp dãy số liệu theo thứ tự không giảm ta được: 6; 6; 7; 7; 7; 8; 8; 8; 9; 10.
Dãy số liệu trên có 10 số liệu nên số trung vị là trung bình cộng của số liệu thứ 5 và 6: Q2 = .
Câu 31:
Thực hiện đo chiều cao (đơn vị cm) của các bạn học sinh tổ 1 của lớp 10D và được ghi lại như sau: 154; 172; 164; 145; 160; 151; 152; 181. Chiều cao trung bình của các bạn tổ 1 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là B
Chiều cao trung bình của tổ 1 là:
.
Câu 32:
Số huy chương vàng trong các giải thể thao quốc tế mà đoàn thể thao Việt Nam trong các giải đấu ở châu Á trong các năm từ 2010 đến 2019 được thống kê trong bảng sau:
|
Năm |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
2017 |
2018 |
2019 |
|
Số huy chương |
39 |
43 |
115 |
52 |
56 |
62 |
130 |
82 |
74 |
120 |
Độ lệch chuẩn của số liệu trên là:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Số trung bình của số liệu trên là:
Khi đó phương sai
Suy ra độ lệch chuẩn là:
.
Câu 33:
Máy bay A bay với vận tốc , máy bay B bay cùng hướng và có tốc độ chỉ bằng một nửa máy bay A. Biểu diễn vectơ vận tốc của máy bay B theo vectơ vận tốc của máy bay A là:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Vì vectơ vận tốc của máy bay B cùng hướng theo vectơ vận tốc của máy bay A và có độ lớn bằng một nửa vectơ nên .
Câu 34:
Khoảng đồng biến và nghịch biến của hàm số y = là:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Tập xác định D = ℝ\{– 1}
Lấy x1, x2 là hai số tùy ý thuộc (– ∞; –1) và (–1; + ∞) sao cho x1 < x2 ta có:
f(x1) – f(x2) =
+) Nếu x1, x2 ∈ (– ∞; –1) thì x1 + 1, x2 + 1 < 0 mà x2 – x1 > 0
Suy ra nên f(x1) > f(x2).
Do đó hàm số đã đồng biến trên (– ∞; –1).
+) Nếu x1, x2 ∈ (–1; + ∞) thì x1 + 1, x2 + 1 > 0 mà x2 – x1 > 0
Suy ra nên f(x1) > f(x2).
Do đó hàm số đã đồng biến trên (–1; + ∞).
Vậy hàm số đồng biến trên các khoảng (– ∞; –1) và (–1; + ∞).
Câu 35:
Tứ giác ABCD có . Khi đó tứ giác ABCD là hình:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Ta có:
⇔
⇔
Do đó và cùng phương nên AB // CD
Vì vậy ABCD là hình thang.
Câu 36:
Cho hình chữ nhật ABCD, M là một điểm bất kì. Chứng minh: .
 Xem đáp án
Xem đáp án
Đáp án đúng là
Gọi O là giao điểm của hai đường chéo AC và BD. Khi đó O là trung điểm của AC và BD. Do đó: và
Ta có:
Suy ra .
Câu 37:
Cho tam giác ABC có và Gọi I là điểm thỏa mãn Tính độ dài đoạn thẳng AI
 Xem đáp án
Xem đáp án
Hướng dẫn giải
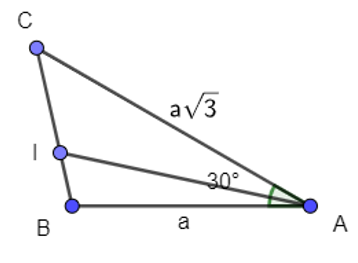
Xét tam giác ABC, có:
nên I thuộc vào đoạn thẳng BC và thỏa mãn IC = 2IB.
Áp dụng định lí cos trong tam giác ABC, ta được:
BC2 = AB2 + AC2 – 2AB.AC.cosA =
⇒ BC = a
⇒ AB = BC = a
⇒ Tam giác ABC cân tại B
⇒
Ta lại có IC = 2IB nên IC = , IB =
Xét tam giác IAC có:
Áp dụng định lí cos, ta được:
IA2 = AC2 + IC2 – 2.AC.IC.cos =
⇔ IA = .
Vậy IA = .
Câu 38:
Cổng chào Yên Lạc có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162 m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10 m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng (tính từ mặt đất đến điểm cao nhất của cổng).
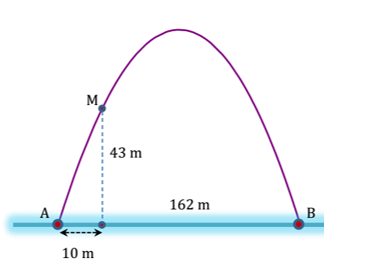
 Xem đáp án
Xem đáp án
Vì cổng có hình dạng parabol nên có phương trình y = ax2 + bx + c (a ≠ 0) (1)
Đặt hệ trục tọa độ như hình vẽ:
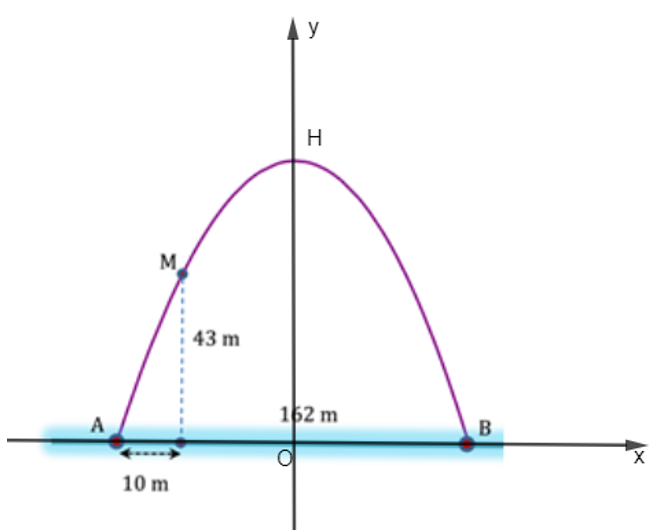
Ta có: A(– 81; 0) và B(81; 0) và M(– 71; 43)
Thay lần lượt tọa độ các điểm vào (1) ta được:
0 = a.(– 81)2 + b(– 81) + c ⇔ 6 561a – 81b + c = 0 (2)
0 = a.812 + b.81 + c ⇔ 6 561a + 81b + c = 0 (3)
43 = a.(– 71)2 + b(– 71) + c ⇔ 5 041 a – 71b + c = 43 (4)
Lấy vế với vế của phương trình (2) trừ (3) ta được: – 162b = 0 ⇔ b = 0.
Khi đó:
(2) ⇔ 6 561a + c = 0
(4) ⇔ 5 041 a + c = 43
Từ đó ta có hệ phương trình:
Suy ra ta có phương trình: y = – 0,03x2 + 185,6.
Điểm H thuộc vào trục Oy nên xH = 0 ⇒ yH = – 0,03.02 + 185,6 = 185,6.
Vì vậy chiều cao của cổng chính là đoạn OH và bằng 185,6 m.
Câu 39:
Nam đo được đường kính của một hình tròn là 24 ± 0,2 cm. Nam tính được chu vi đường tròn là C = 75,36. Hãy ước lượng sai số tuyệt đối của C, biết 3,141 < π < 3,142.
 Xem đáp án
Xem đáp án
Gọi và lần lượt là đường kính và chu vi của đường tròn.
Ta có: 24 – 0,2 ≤ ≤ 24 + 0,2 hay 23,8 ≤ ≤ 24,2
Suy ra 3,141.23,8 ≤ .π ≤ 24,2.3,42 ⇔ 74,7558 ≤ ≤ 76,0364
⇔ 74,7558 – 75,36 ≤ – 75,36 ≤ 76,0364 – 75,36
⇔ – 0,6042 ≤ – 75,36 ≤ 0,6764.
Vậy sai số tuyệt đối của C nằm trong khoảng từ – 0,6042 đển 0,6764.
