Trắc nghiệm Toán 10 Bài 1. Mệnh đề có đáp án
-
1517 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Trong các câu sau, câu nào là mệnh đề?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Chỉ có câu “Trung Quốc là nước đông dân nhất thế giới” có thể xác định được tính đúng sai nên đáp án B là mệnh đề.
Câu 2:
Trong các câu sau, câu nào không phải là mệnh đề?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đáp án A là câu cảm thán không xác định được tính đúng sai. Do đó không phải là mệnh đề.
Câu 3:
Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Hãy đi nhanh lên!
b) Hà Nội là thủ đô của Việt Nam.
c) 4 + 5 + 7 = 15.
d) Năm 2018 là năm nhuận.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Câu a) là câu cảm thán không xác định được tính đúng, sai nên câu a không phải là mệnh đề.
Các câu b), c), d) đều có thể xác định được tính đúng sai. Do đó các câu b), c), d) đều là mệnh đề.
Vậy có tất cả 3 mệnh đề.
Câu 4:
Câu nào sau đây không là mệnh đề?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì x > 2 là mệnh đề chứa biến không xác định được tính đúng sai nên không phải mệnh đề.
Câu 5:
Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
A là mệnh đề sai: Ví dụ: 1 + 3 = 4 là số chẵn nhưng 1, 3 là số lẻ.
B là mệnh đề sai: Ví dụ: 2.3 = 6 là số chẵn nhưng 3 là số lẻ.
C là mệnh đề sai: Ví dụ: 1 + 3 = 4 là số chẵn nhưng 1, 3 là số lẻ.
Câu 6:
Cho mệnh đề A: “\[\forall x \in \mathbb{R},{x^2} - x + 7 < 0\]”. Mệnh đề phủ định của A là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Phủ định của \[\forall \] là \[\exists \]
Phủ định của < là ≥
Do đó phủ định của mệnh đề A: “\[\forall x\in \mathbb{R},{{x}^{2}}-x+7<0\]” là
\(\overline A \): “\[\exists x \in \mathbb{R},{x^2} - x + 7 \ge 0\]”.
Câu 7:
Mệnh đề phủ định của mệnh đề là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Phủ định của \[\forall \] là \[\exists \]
Phủ định của > là ≤
Do đó mệnh đề phủ định của mệnh đề đã cho là “\(\exists x \in \mathbb{R},\,{x^2} + x + 5 \le 0\)”
Câu 8:
Phủ định của mệnh đề là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Phủ định của\[\forall \]là \[\exists \]
Phủ định của = là ≠.
Do đó mệnh đề phủ định của mệnh đề đã cho là: .
Câu 9:
Với giá trị thực nào của x mệnh đề chứa biến P(x): “2x2 – 1 < 0” là mệnh đề đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
P(0) = 2.02 – 1 < 0 hay -1 < 0 (đúng). Do đó với x = 0 ta được một mệnh đề đúng.
P(5) = 2.52 – 1 < 0 hay 49 < 0 (sai). Do đó với x = 5 ta được một mệnh đề sai.
P(1) = 2.12 – 1 < 0 hay 1 < 0 (sai). Do đó với x = 1 ta được một mệnh đề sai.
P(\[\frac{4}{5}\]) = 2.\[{\left( {\frac{4}{5}} \right)^2}\] – 1 < 0 hay \(\frac{7}{{25}} < 0\) (sai). Do đó với x = \[\frac{4}{5}\] ta được một mệnh đề sai.
Câu 10:
Mệnh đề nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tam giác ABC có \(\widehat {\rm{A}}{\rm{ = }}\,{\rm{6}}{{\rm{0}}^0}\) chưa đủ điều kiện để tam giác ABC là tam giác đều. Do đó B sai.
Câu 11:
Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
- Vì \({x^2} - x + 1 = {\left( {x - \frac{1}{2}} \right)^2} + \frac{3}{4} > 0,\forall x \in \mathbb{R}\). Do đó mệnh đề A đúng.
- Ta có n ≥ 0 với mọi \(n \in \mathbb{N}\). Do đó mệnh đề B sai.
- Xét n2 = 2 \( \Leftrightarrow \left[ \begin{array}{l}n = \sqrt 2 \\n = - \sqrt 2 \end{array} \right.\) mà \(\sqrt 2 ; - \sqrt 2 \notin \mathbb{Q}\). Do đó C sai.
- Chọn x = –1 \( \in \mathbb{Z}\) khi đó \(\frac{1}{{ - 1}} = - 1 < 0\). Do đó D sai.Câu 12:
Mệnh đề \[\forall x \in \mathbb{R},{x^2} - 2 + {\rm{a}} > 0\] với a là số thực cho trước. Tìm a để mệnh đề đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì x2 ≥ 0, \(\forall x \in \mathbb{R}\) nên để x2 – 2 + a > 0 khi – 2 + a > 0 ⇔ a > 2.
Câu 13:
Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
- Mệnh đề đảo của A là: Nếu a + b chia hết cho c thì a và b cùng chia hết cho c.
Chọn a = 5, b = 2, c = 7 thì a + b = 5 + 2 = 7 chia hết cho c = 7. Nhưng 2 không chia hết cho 7 và 5 cũng không chia hết cho 7. Do đó mệnh đề đảo của A sai.
- Mệnh đề đảo của B là: Nếu hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau.
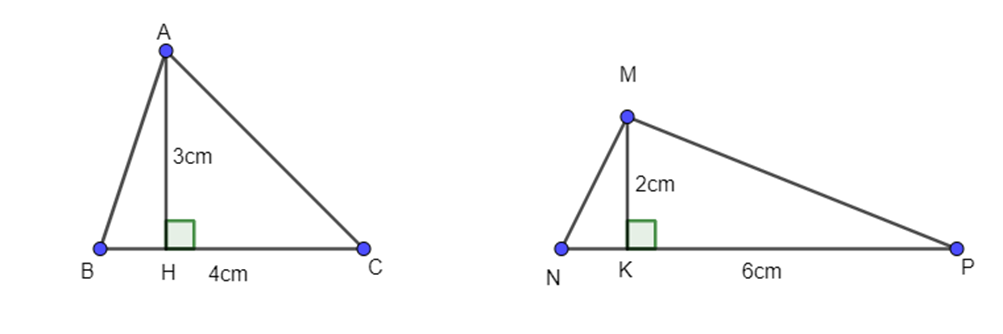
Hai tam giác ABC và MNP có cùng diện tích là 12 cm2. Tuy nhiên hai tam giác này không bằng nhau. Do đó mệnh đề đảo của B là sai.
- Mệnh đề đảo của C là: “Nếu a chia hết cho 9 thì a chia hết cho 3” là mệnh đề đúng.
- Mệnh đề đảo của D là: “Nếu số đó chia hết cho 5 thì số đó có chữ số tận cùng là 0”. Ví dụ số 25 chia hết cho 5 nhưng số này có tận cùng là 5 chứ không phải 0. Do đó mệnh đề đảo của D sai.
Câu 14:
Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đáp án A: Mệnh đề P : “– π2 ≈ – 9.8 < – 2” nên P đúng; mệnh đề Q : “π2 ≈ 9.8 > 4” nên mệnh đề Q sai. Mà đề kéo theo chỉ sai khi P đúng Q sai.
Vậy mệnh đề ở đáp án A sai.
Đáp án B: Mệnh đề P : “π ≈ 3.14 < 4” nên P đúng; mệnh đề Q : “π2 ≈ 9.8 < 16” mệnh đề Q đúng
Vậy mệnh đề ở đáp án B đúng.
Đáp án C: Mệnh đề P :“\(\sqrt {23} \simeq 4,8 < 5\)” nên mệnh đề P đúng; mệnh đề Q :“\(\,2\sqrt {23} \simeq 9,6 < 10\)” nên mệnh đề Q đúng
Vậy mệnh đề ở đáp án C đúng.
Đáp án D : Mệnh đề P :“\(\sqrt {23} \simeq 4,8 < 5\)” nên P đúng; mệnh đề Q :“\( - \,2\sqrt {23} \simeq - 9,6 > - 10\)” mệnh đề Q đúng.
Vậy mệnh đề ở đáp án D đúng.
Câu 15:
Cho mệnh đề chứa biến P(x): "x + 15 ≤ x2" với giá trị thực nào của x trong các giá trị sau P(x) là mệnh đề đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
A. P(0): "0 + 15 ≤ 02"(Sai). Do đó với x = 0 mệnh đề sai.
B. P(3): "3 + 15 ≤ 32"(Sai). Do đó với x = 3 mệnh đề sai
C. P(4): "4 + 15 ≤ 42"(Sai). Do đó với x = 4 mệnh đề sai.
D. P(5): "5 + 15 ≤ 52"(Đúng). Do đó với x = 5 ta được mệnh đề đúng.
Câu 16:
Cho hai số \({\rm{a}} = \sqrt {10} + 1\), \({\rm{b}} = \sqrt {10} - 1\). Hãy chọn khẳng định đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có a2 + b2 = (\(\sqrt {10} \)+ 1)2 + (\(\sqrt {10} \)- 1)2 = 10 + 2\(\sqrt {10} \) + 1 + 10 – 2\(\sqrt {10} \) +1 = 22 \( \in \mathbb{N}\). Do đó đáp án A đúng, C sai
Ta lại có a + b = \(\sqrt {10} \)+1 +\(\sqrt {10} \) – 1 = \(2\sqrt {10} \notin \mathbb{Q}\). Do đó đáp án B sai.
Ta có: a.b = (\(\sqrt {10} \)+ 1)( \(\sqrt {10} \)– 1) =10 – \(\sqrt {10} \)+\(\sqrt {10} \)– 1 = 9. Do đó đáp án D sai.
