Hướng dẫn giải

Đáp án đúng là: C

Ta có :  $\overrightarrow a$ + $\overrightarrow b$ = (2 + (– 5); – 4 + 3) = (– 3; – 1).

Hướng dẫn giải

Đáp án đúng là : A

Ta có : $\overrightarrow m - \overrightarrow n$ = (3 – (– 1)); – 4 – 2) = (4; – 6).

Hướng dẫn giải

Đáp án đúng là : B

Ta có: 2$\overrightarrow m$= 2(–1; 2) = (–2; 4)

2$\overrightarrow m + \overrightarrow n$ = (– 2 + 5); 4 – 7) = (3; – 3).

Hướng dẫn giải

Đáp án đúng là : A

Tọa độ điểm I là nghiệm của hệ phương trình: $\left\{ \begin{array}{l}{x_I} = \frac{{ - 1 + 1}}{2} = 0\\{y_I} = \frac{{1 + 1}}{2} = 1\end{array} \right. \Rightarrow I\left( {0;1} \right)$.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: 3$\overrightarrow k$= 3(5 ; 2) = (15 ; 6) ; 2$\overrightarrow n$ = 2(10 ; 8) = (20 ; 16)

$3\overrightarrow k - 2\overrightarrow n$ = (15 – 20 ; 6 – 16) = (– 5; – 10).

Hướng dẫn giải

Đáp án đúng là : B

Ta có $\left\{ \begin{array}{l}\overrightarrow {AB} = \left( { - 2; - 1} \right)\\\overrightarrow {AC} = \left( { - 3; - 2} \right)\end{array} \right.$ $\Rightarrow$$\overrightarrow {AB} - \overrightarrow {AC}$ = (– 2 – (– 3); – 1 – (– 2)) = (1; 1).

Hướng dẫn giải

Đáp án đúng là : C

Gọi điểm B có tọa độ (x_B ; y_B)

Vì I là trung điểm của AB nên ta có :

 $\left\{ \begin{array}{l}{x_I} = \frac{{2 + {x_B}}}{2} = 4\\{y_I} = \frac{{ - 3 + {y_B}}}{2} = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = 2.4 - 2 = 6\\{y_I} = 2.7 - ( - 3) = 17\end{array} \right.$ $\Rightarrow$ B(6; 17).

Hướng dẫn giải

Đáp án đúng là : D

Gọi toạ độ trọng tâm G (${x_G}$; ${y_G}$), ta có :

 $\left\{ \begin{array}{l}{x_G} = \frac{{3 + 1 + 5}}{3} = 3\\{y_G} = \frac{{5 + 2 + 2}}{3} = 3\end{array} \right.$ $\Rightarrow$G (3; 3).

Hướng dẫn giải

Đáp án đúng là : C

Gọi toạ độ C(x ; y), ta có:

Vì G là trọng tâm tam giác ABC nên : $\left\{ \begin{array}{l}{x_G} = \frac{{6 + \left( { - 3} \right) + x}}{3} = - 1\\{y_G} = \frac{{1 + 5 + y}}{3} = 1\end{array} \right.$

$\Rightarrow$$\left\{ \begin{array}{l}x = - 6\\y = - 3\end{array} \right..$ hay C (–6; –3).

Hướng dẫn giải

Đáp án đúng là: B

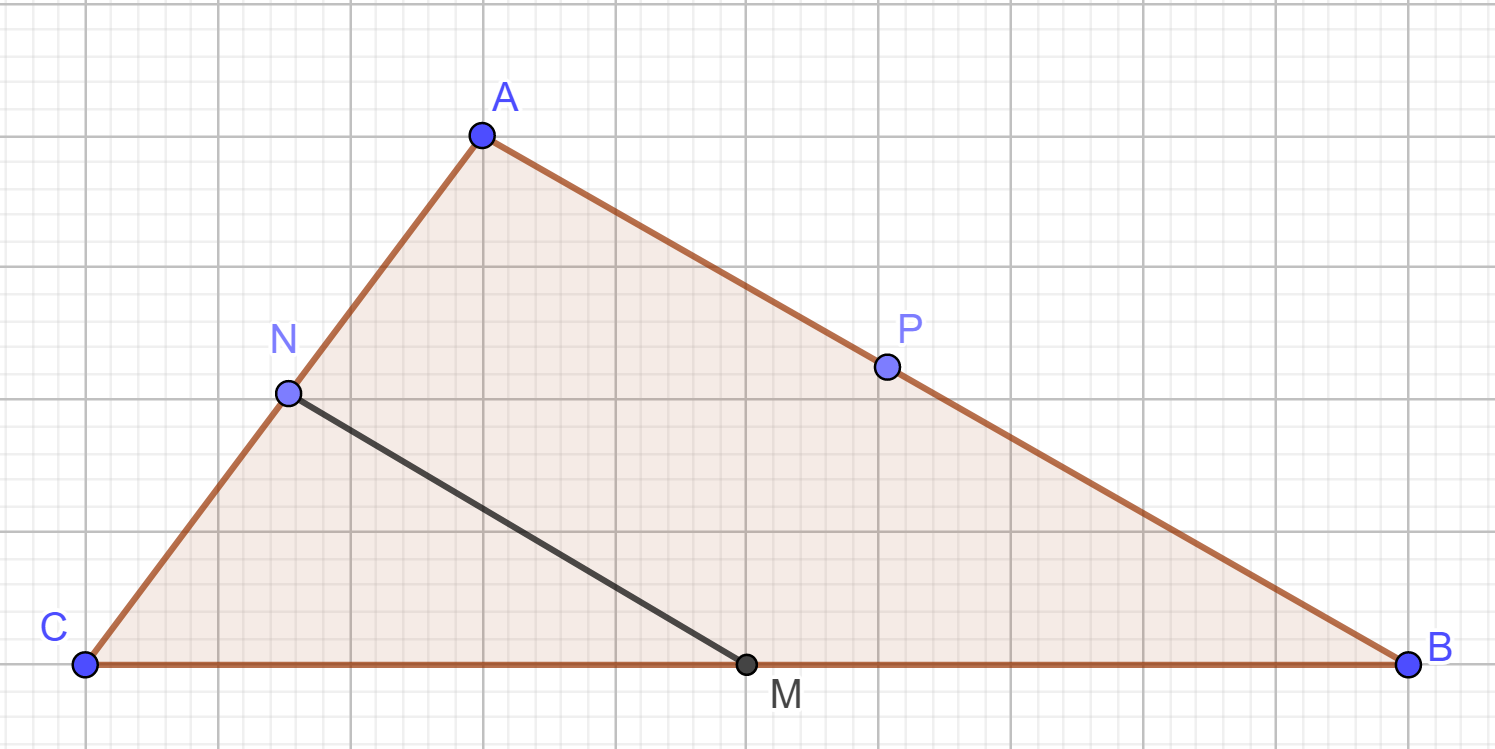
Gọi toạ độ A (x ; y).

Ta có : $\overrightarrow {PA}$ = (x + 1; y – 6) và $\overrightarrow {MN}$ = (–2; –7)

Theo tính chất đường trung bình tam giác, ta có:

$\overrightarrow {MN}$= $\frac{1}{2}$$\overrightarrow {AB}$ = $\overrightarrow {PA}$

Khi đó (1)$\Leftrightarrow$$\left\{ \begin{array}{l}x + 1 = - 2\\y - 6 = - 7\end{array} \right.$ $\Leftrightarrow$$\left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.$

Hay A (–3; –1).

Hướng dẫn giải

Đáp án đúng là : B

Xét tam giác ABC, có :

M là trung điểm AB

N là trung điểm AC

Suy ra MN là đường trung bình tam giác ABC

Theo tính chất đường trung bình, ta có :

$\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC}$ = $\frac{1}{2}$.(2; –8) = (1; –4).

Hướng dẫn giải

Đáp án đúng là : B

Vì M là trung điểm BC nên ta có : $\left\{ \begin{array}{l}{x_B} = 2{x_M} - {x_C}\\{y_B} = 2{y_M} - {y_C}\end{array} \right.$

$\Leftrightarrow$$\left\{ \begin{array}{l}{x_B} = 2.2 - \left( { - 2} \right) = 6\\{y_B} = 2.0 - \left( { - 4} \right) = 4\end{array} \right.$$\Rightarrow$B (6; 4).

Vì G là trọng tâm tam giác ABC nên $\left\{ \begin{array}{l}{x_A} = 3{x_G} - {x_B} - {x_C}\\{y_A} = 3{y_G} - {y_B} - {y_C}\end{array} \right.$

$\Leftrightarrow$$\left\{ \begin{array}{l}{x_A} = 3.0 - 6 - ( - 2)\\{y_A} = 3.4 - 4 - ( - 4)\end{array} \right.$$\Leftrightarrow$$\left\{ \begin{array}{l}{x_A} = - 4\\{y_A} = 12\end{array} \right.$ hay A (–4 ; 12).

Suy ra ${x_A} + {x_B}$= 6 + (–4) = 2.

Hướng dẫn giải

Đáp án đúng là : C

Vì O là trọng tâm tam giác ABC nên, ta có : $\left\{ \begin{array}{l}{x_G} = \frac{{ - 2 + x + 3 + x}}{3} = 0\\{y_G} = \frac{{2 + 5 + 2y + 3 - y}}{3} = 0\end{array} \right.$

$\Rightarrow$$\left\{ \begin{array}{l}x = - \frac{1}{2}\\y = - 10\end{array} \right. \Rightarrow 2.x + y = 2.\left( { - \frac{1}{2}} \right) + \left( { - 10} \right) = - 11$.

Hướng dẫn giải

Đáp án đúng là : C

Gọi toạ độ điểm C (x ; y).

Vì G là trọng tâm tam giác ABC nên ta có : $\left\{ \begin{array}{l}{x_G} = \frac{{6 + \left( { - 3} \right) + x}}{3} = - 1\\{y_G} = \frac{{1 + 5 + y}}{3} = 1\end{array} \right.$

$\Rightarrow$$\left\{ \begin{array}{l}x = - 6\\y = - 3\end{array} \right.$ hay C (–6; –3).

Hướng dẫn giải

Đáp án đúng là : B

Ta có : $\overrightarrow a - \overrightarrow b$ = (–2m; 2) – (2; –7n) = (–2m –2; 2 + 7n)

Mà $\overrightarrow a - \overrightarrow b$ = (6; – 5)

Nên ta có: $\left\{ \begin{array}{l} - 2m - 2 = 6\\2 + 7n = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 4\\n = - 1\end{array} \right.$

Vậy m = – 4 và n = – 1.