15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án

Câu 1:

Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 9 \sqrt{3}$

B. $S_{Δ A B C} = \frac{9 \sqrt{3}}{2}$

C. $S_{Δ A B C} = 9$

D. $S_{Δ A B C} = \frac{9}{2}$

Xem đáp án

Đáp án đúng là: B

Ta có: $S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} .3.6. \sin 60^{0} = \frac{9 \sqrt{3}}{2}$ (đơn vị diện tích)

Câu 2:

Tam giác ABC có $A C = 4, \hat{B A C} = 30 °, \hat{A C B} = 75 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 8$

B. $S_{Δ A B C} = 4 \sqrt{3}$

C. $S_{Δ A B C} = 4$

D. $S_{Δ A B C} = 8 \sqrt{3}$

Xem đáp án

Đáp án đúng là: C

Ta có: $\hat{A B C} = 180^{0} - (\hat{B A C} + \hat{A C B}) = 75 ° = \hat{A C B}$ .

Suy ra tam giác ABC cân tại A nên $A B = A C = 4$ .

Diện tích tam giác ABC là $S_{Δ A B C} = \frac{1}{2} A B . A C \sin \hat{B A C} = 4$ (đơn vị diện tích)

Câu 3:

Tam giác ABC có a = 21, b = 17, c = 10 .Diện tích của tam giác ABC bằng:

A. $S_{Δ A B C} = 16$

B. $S_{Δ A B C} = 48$

C. $S_{Δ A B C} = 24$

D. $S_{Δ A B C} = 84$

Xem đáp án

Đáp án đúng là: D

Ta có:

Nửa chu vi của tam giác ABC là:

$p = \frac{21 + 17 + 10}{2} = 24$ (đơn vị độ dài).

Do đó

Diện tích tam giác ABC là:

$S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{24 (24 - 21) (24 - 17) (24 - 10)} = 84$ (đơn vị diện tích).

Câu 4:

Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 60 °$ . Tính độ dài đường cao h kẻ từ đỉnh A xuống cạnh BC của tam giác.

A. $h = 3 \sqrt{3}$

B. $h = \sqrt{3}$

C. $h = 3$

D. $h = \frac{3}{2}$

Xem đáp án

Đáp án đúng là: C

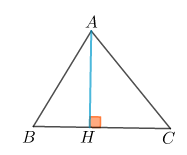
Áp dụng định lý hàm số cosin, ta có:

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C \cos A = 27 \Rightarrow B C = 3 \sqrt{3}$ (đơn vị độ dài).

Ta có: $S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} .3.6. \sin 60^{0} = \frac{9 \sqrt{3}}{2}$ (đơn vị diện tích).

Lại có $S_{Δ A B C} = \frac{1}{2} . B C . h_{a} \Rightarrow h_{a} = \frac{2 S}{B C} = 3$ (đơn vị độ dài).

Câu 5:

Tam giác ABC có $A C = 4, \hat{A C B} = 60 °$ . Tính độ dài đường cao h xuất phát từ đỉnh A của tam giác.

A. $h = 2 \sqrt{3}$

B. $h = 4 \sqrt{3}$

C. $h = 2$

D. $h = 4$

Xem đáp án

Đáp án đúng là: A

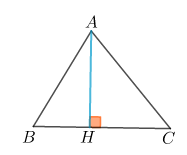
Gọi H là chân đường cao xuất phát từ đỉnh A.

Xét tam giác vuông AHC:

$\sin \hat{A C H} = \frac{A H}{A C} \Rightarrow A H = A C . \sin \hat{A C H} = 4. \frac{\sqrt{3}}{2} = 2 \sqrt{3}$ (đơn vị độ dài)

Câu 6:

Tam giác ABC có a = 21, b = 17, c = 10 . Gọi B’ là hình chiếu vuông góc của B trên cạnh AC. Tính BB’.

A. $B B' = 8$

B. $B B' = \frac{84}{5}$

C. $B B' = \frac{168}{17}$

D. $B B' = \frac{84}{17}$

Xem đáp án

Đáp án đúng là: C

Ta có:

Nửa chu vi là:

$p = \frac{21 + 17 + 10}{2} = 24$ (đơn vị độ dài).

Suy ra $S = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{24 (24 - 21) (24 - 17) (24 - 10)} = 84$ (đơn vị diện tích).

Lại có $S = \frac{1}{2} b . B B' \Leftrightarrow 84 = \frac{1}{2} .17. B B' \Leftrightarrow B B' = \frac{168}{17}$ (đơn vị độ dài).

Câu 7:

Tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng $64 {cm}^{2}$ . Giá trị sinA bằng:

A. $\sin A = \frac{\sqrt{3}}{2}$

B. $\sin A = \frac{3}{8}$

C. $\sin A = \frac{4}{5}$

D. $\sin A = \frac{8}{9}$

Xem đáp án

Đáp án đúng là: D

Ta có:

$S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{B A C} \Leftrightarrow 64 = \frac{1}{2} .8.18. \sin A \Leftrightarrow \sin A = \frac{8}{9} .$

Câu 8:

Hình bình hành ABCD có $A B = a, B C = a \sqrt{2}$ và $\hat{B A D} = 45^{0}$ . Khi đó hình bình hành có diện tích bằng:

A. $2 a^{2}$

B. $a^{2} \sqrt{2}$

C. $a^{2}$

D. $a^{2} \sqrt{3}$

Xem đáp án

Đáp án đúng là: C

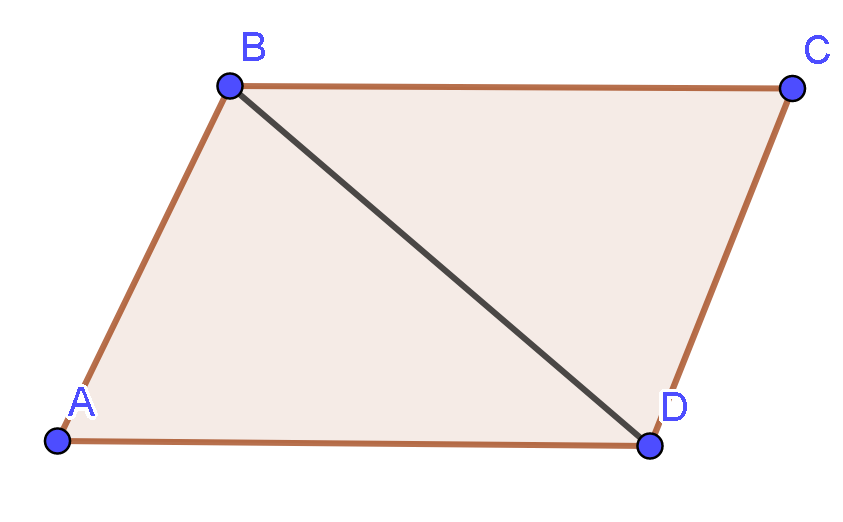
Diện tích tam giác ABD là: $S_{Δ A B D} = \frac{1}{2} . A B . A D . \sin \hat{B A D} = \frac{1}{2} . a . a \sqrt{2} . \sin 45^{0} = \frac{a^{2}}{2}$ (đơn vị diện tích).(BC = AD = a $\sqrt{2}$ )

Vậy diện tích hình bình hành ABCD là $S_{A B C D} = 2. S_{Δ A B D} = 2. \frac{a^{2}}{2} = a^{2}$ (đơn vị diện tích)

Câu 9:

Tam giác ABC vuông tại A có AB = AC = 30cm. Hai đường trung tuyến BF và CE cắt nhau tại G. Diện tích tam giác GFC bằng:

A. ${50 cm}^{2}$

B. $50 \sqrt{2} {cm}^{2};$

C. ${75 cm}^{2}$

D. $15 \sqrt{105} {cm}^{2}$

Xem đáp án

Đáp án đúng là: C

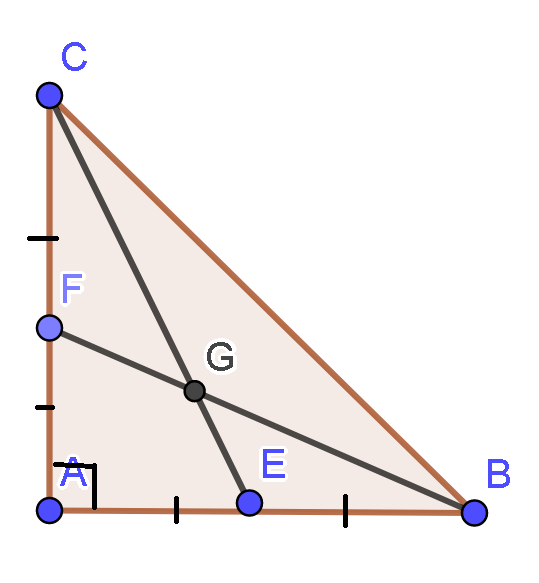
Vì F là trung điểm của AC $\Rightarrow F C = \frac{1}{2} A C = 15 c m .$

Đường thẳng BF cắt CE tại G suy ra G là trọng tâm tam giác ABC.

Khi đó: $\frac{d (B; (A C))}{d (G; (A C))} = \frac{B F}{G F} = 3 \Rightarrow d (G; (A C)) = \frac{1}{3} d (B; (A C)) = \frac{A B}{3} = 10 c m .$

Vậy diện tích tam giác GFC là:

$S_{Δ G F C} = \frac{1}{2} . d (G; (A C)) . F C = \frac{1}{2} .10.15 = 75 c m^{2} .$

Câu 10:

Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:

A. $13 {cm}^{2}$

B. $13 \sqrt{2} {cm}^{2}$

C. $12 \sqrt{3} {cm}^{2};$

D. ${15 cm}^{2};$

Xem đáp án

Đáp án đúng là: C

Xét tam giác ABC đều, có độ dài cạnh bằng a.

Theo định lí sin, ta có: $\frac{B C}{\sin \hat{B A C}} = 2 R \Leftrightarrow \frac{a}{\sin 60^{0}} = 2.4 \Leftrightarrow a = 8. \sin 60^{0} = 4 \sqrt{3}$ (đơn vị độ dài).

Vậy diện tích cần tính là:

$S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{B A C} = \frac{1}{2} . {(4 \sqrt{3})}^{2} . \sin 60^{0} = 12 \sqrt{3} c m^{2} .$

Câu 11:

Tam giác ABC có $B C = 2 \sqrt{3}, A C = 2 A B$ và độ dài đường cao AH = 2. Tính độ dài cạnh AB.

A. AB = 2;

B.

A B = \frac{2 \sqrt{3}}{3}

;

C. AB = 2 hoặc

A B = \frac{2 \sqrt{21}}{3}

;

D. AB = 2 hoặc

A B = \frac{2 \sqrt{3}}{3}

.

Xem đáp án

Đáp án đúng là: C

Nửa chu vi là:

Ta có: $p = \frac{A B + B C + C A}{2} = \frac{2 \sqrt{3} + 3 A B}{2}$ .

Suy ra $S = \sqrt{(\frac{3 A B + 2 \sqrt{3}}{2}) (\frac{3 A B - 2 \sqrt{3}}{2}) (\frac{2 \sqrt{3} - A B}{2}) (\frac{2 \sqrt{3} + A B}{2})}$ .

Lại có $S = \frac{1}{2} B C . A H = 2 \sqrt{3}$ (đơn vị diện tích).

Từ đó ta có: $2 \sqrt{3} = (\frac{3 A B + 2 \sqrt{3}}{2}) (\frac{3 A B - 2 \sqrt{3}}{2}) (\frac{2 \sqrt{3} - A B}{2}) (\frac{2 \sqrt{3} + A B}{2})$

$\Leftrightarrow 12 = \frac{(9 A B^{2} - 12) (12 - A B^{2})}{16} \Leftrightarrow [\begin{array}{l} A B = 2 \\ A B = \frac{2 \sqrt{21}}{3} \end{array} .$

Câu 12:

Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:

A. 2S;

B. 3S;

C. 4S;

D. 6S.

Xem đáp án

Đáp án đúng là: D

Diện tích tam giác ABC ban đầu là: $S = \frac{1}{2} . A C . B C . \sin \hat{A C B} = \frac{1}{2} . a b . \sin \hat{A C B} .$

Khi tăng cạnh BC lên 2 lần và cạnh AC lên 3 lần thì diện tích tam giác ABC lúc này là:

$S_{Δ A B C} = \frac{1}{2} . (3 A C) . (2 B C) . \sin \hat{A C B} = 6. \frac{1}{2} . A C . B C . \sin \hat{A C B} = 6 S .$

Câu 13:

Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

A. $60^{0}$

B. $90^{0}$

C. $150^{0}$

D. $120^{0}$

Xem đáp án

Đáp án đúng là: B

Diện tích tam giác ABC là: $S_{Δ A B C} = \frac{1}{2} . A C . B C . \sin \hat{A C B} = \frac{1}{2} . a b . \sin \hat{A C B} .$

Vì a, b dương và $\sin \hat{A C B} \leq 1$ nên suy ra $S_{Δ A B C} \leq \frac{a b}{2} .$

Dấu $" = "$ xảy ra khi và chỉ khi $\sin \hat{A C B} = 1 \Leftrightarrow \hat{A C B} = 90^{0} .$

Vậy giá trị lớn nhất của diện tích tam giác ABC là $S = \frac{a b}{2}$ (đơn vị diện tích).

Câu 14:

Tam giác cân có cạnh bên bằng a và góc ở đỉnh bằng α thì có diện tích là

A. $\frac{a^{2} \cos α}{2}$

B. $\frac{a^{2} \sin α}{2}$

C. $a^{2} \cos α$

D. $a^{2} \sin α$

Xem đáp án

Đáp án đúng là: B

Giả sử tam ABC cân taị C, ta có: AC = BC = a; $\hat{C}$ = $α$

Diện tích tam giác là: S = $\frac{1}{2}$ a.b.sinC = $\frac{1}{2}$ .a.a.sin $α$ = $\frac{1}{2}$ $a^{2}$ sin $α$ .

Câu 15:

Tam giác ABC có $A B = 3, A C = 6, \hat{B A C} = 30 °$ . Tính diện tích tam giác ABC.

A. $S_{Δ A B C} = 9 \sqrt{3}$

B. $S_{Δ A B C} = \frac{9 \sqrt{3}}{2}$

C. $S_{Δ A B C} = 4, 5;$

D. $S_{Δ A B C} = \frac{9}{2}$

Xem đáp án

Đáp án đúng là: C

Ta có: $S_{Δ A B C} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} .3.6. \sin 30^{0} = \frac{9.1}{2}$ = 4,5 (đơn vị diện tích).

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án

Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương