Trắc nghiệm Toán 10 Bài 2. Tập hợp. Các phép toán trên tập hợp (phần 2) có đáp án
Trắc nghiệm Toán 10 Bài 2. Tập hợp. Các phép toán trên tập hợp (Thông hiểu) có đáp án
-
799 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Liệt kê các phần tử của tập hợp E = {x ∈ ℕ| 2x2 – 3x + 1 = 0}:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Các phần tử của tập hợp E là các nghiệm là số tự nhiên của phương trình 2x2 – 3x + 1 = 0.
Giải phương trình 2x2 – 3x + 1 = 0 ta được các nghiệm là x = 1, x = \(\frac{1}{2}\).
Vì 1 ∈ ℕ và \(\frac{1}{2}\) ∉ ℕ.
Do đó, chỉ có 1 là phần tử của tập hợp E.
Ta viết E = {1}.
Vậy đáp án đúng là đáp án A.
Câu 2:
Cho tập hợp A = {1; 3; 5; 7}. Tập hợp A có bao nhiêu tập con có hai phần tử?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Các tập con có hai phần tử của tập A là:
{1; 3}, {1; 5}, {1; 7}, {3; 5}, {3; 7}, {5; 7}.
Vậy có 6 tập con có hai phần tử của tập A.
Câu 3:
Cho các tập hợp A = {1; 5}, B = {1; 3; 5}. Chọn kết quả đúng trong các kết quả sau:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có: A ∩ B = {x ∈ A và x ∈ B}
Các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B là: 1, 5.
Do đó, A ∩ B = {1; 5}.
Câu 4:
Cho tập hợp C = [–5; 3), D = (1; +∞). Khi đó C ∩ D là tập nào sau đây?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Để xác định tập hợp C ∩ D, ta biểu diễn tập hợp C và D lên trục số như sau:
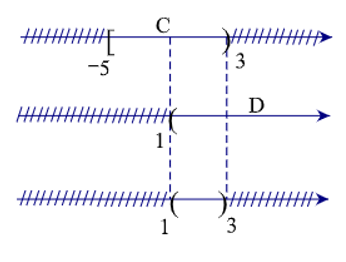
Từ sơ đồ, ta thấy C ∩ D = (1; 3).
Câu 5:
Cho A = (– ∞; – 2], B = [3; + ∞), C = (0; 4). Khi đó tập (A ∪ B) ∩ C là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có: A ∪ B = (– ∞; – 2) ∪ [3; + ∞)
(A ∪ B) ∩ C = (– ∞; – 2) ∪ [3; + ∞) ∩ (0; 4) = [3; 4).
Câu 6:
Cho hai tập hợp A = {x ∈ ℤ| (x2 – 10x + 21)(x3 – x) = 0}, B = {x ∈ ℤ| – 3 < 2x + 1 < 5}. Khi đó tập X = A \ B là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
+ Giải phương trình (x2 – 10x + 21)(x3 – x) = 0 ⇔\[\left[ {\begin{array}{*{20}{c}}{{x^2} - 10x + 21 = 0}\\{{x^3} - x = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left[ {\begin{array}{*{20}{c}}{x = 3}\\{x = 7}\end{array}} \right.}\\{\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \pm 1}\end{array}} \right.}\end{array}} \right.\].
Mà x ∈ ℤ nên A = {– 1; 0; 1; 3; 7}.
+ Giải bất phương trình – 3 < 2x + 1 < 5 ⇔ – 2 < x < 2. Mà x ∈ ℤ nên B = {– 1; 0; 1}.
Khi đó X = A \ B = {x| x ∈ A, x ∉ B} = {3; 7}.
Câu 7:
Cho hai tập hợp A = {1; 2; 4; 6} và B = {1; 2; 3; 4; 5; 6; 7; 8}. Xác định tập CBA.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có: CBA = B \ A = {x| x ∈ B, x ∉ A} = {3; 5; 7; 8}.
Các phần tử thuộc tập B nhưng không thuộc tập A là: 3; 5; 7; 8.
Vậy CBA = {3; 5; 7; 8}.
Câu 8:
Cho tập hợp H = (– ∞; 3) ∪ [9; + ∞). Hãy viết lại tập hợp H dưới dạng nêu tính chất đặc trưng.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có: A = (– ∞; 3) = {x ∈ ℝ| x < 3}
B = [9; + ∞) = {x ∈ ℝ| x ≥ 9}
Mà H = A ∪ B = {x | x ∈ A hoặc x ∈ B}.
Do đó, H = {x ∈ ℝ| x < 3 hoặc x ≥ 9}.