Trắc nghiệm Toán 10 CTST Bài 2. Định lí côsin và định lí sin có đáp án (Phần 2)
Trắc nghiệm Toán 10 CTST Bài 2. Định lí côsin và định lí sin có đáp án (Thông hiểu)
-
709 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
∆ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Nửa chu vi của tam giác ABC là:
\(p = \frac{{a + b + c}}{2} = \frac{{21 + 17 + 10}}{2} = 24\).
Diện tích tam giác ABC là:
\({S_{\Delta ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)
\( = \sqrt {24\left( {24 - 21} \right)\left( {24 - 17} \right)\left( {24 - 10} \right)} = 84\) (đơn vị diện tích)
Vậy ta chọn phương án D.
Câu 2:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Nửa chu vi của ∆ABC là: \(p = \frac{{a + b + c}}{2} = \frac{{5 + 6 + 7}}{2} = 9\).
Diện tích của ∆ABC là:
\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)
\( = \sqrt {9\left( {9 - 5} \right)\left( {9 - 6} \right)\left( {9 - 7} \right)} = 6\sqrt 6 \) (đơn vị diện tích)
Ta có S = p.r
\( \Leftrightarrow r = \frac{S}{p} = \frac{{6\sqrt 6 }}{9} = \frac{{2\sqrt 6 }}{3}\).
Vậy ta chọn phương án C.
Câu 3:
∆ABC có AB = 3, AC = 6 và \(\widehat A = 60^\circ \). Độ dài bán kính R của đường tròn ngoại tiếp ∆ABC bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Áp dụng định lí côsin cho DABC, ta có:
BC2 = AB2 + AC2 –2.AB.AC.cosA
= 32 + 62 – 2.3.6.cos60°
= 27.
Suy ra \(BC = \sqrt {27} = 3\sqrt 3 \).
Áp dụng định lí sin, ta có \(\frac{{BC}}{{\sin A}} = 2R\).
Suy ra \(R = \frac{{BC}}{{2.\sin A}} = \frac{{3\sqrt 3 }}{{2.\sin 60^\circ }} = 3\).
Vậy ta chọn phương án A.
Câu 4:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có ∆ABC đều cạnh a.
Suy ra AB = AC = BC = a.
Nửa chu vi ∆ABC là: \(p = \frac{{a + a + a}}{2} = \frac{{3a}}{2}\).
Diện tích ∆ABC là:
\(S = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} \)
\( = \sqrt {\frac{{3a}}{2}\left( {\frac{{3a}}{2} - a} \right)\left( {\frac{{3a}}{2} - a} \right)\left( {\frac{{3a}}{2} - a} \right)} \)
\( = \sqrt {\frac{{3a}}{2}.\frac{a}{2}.\frac{a}{2}.\frac{a}{2}} = \frac{{{a^2}.\sqrt 3 }}{4}\) (đơn vị diện tích)
Ta có \(S = \frac{{AB.AC.BC}}{{4R}}\).
Suy ra \(R = \frac{{AB.AC.BC}}{{4S}} = \frac{{a.a.a}}{{4.\frac{{{a^2}.\sqrt 3 }}{4}}} = \frac{{a\sqrt 3 }}{3}\).
Vậy ta chọn phương án C.
Câu 5:
∆ABC có AB = 5, AC = 10, \(\widehat A = 60^\circ \). Độ dài đường cao ha của ∆ABC bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Áp dụng định lí côsin cho DABC, ta có:
BC2 = AB2 + AC2 – 2AB.AC.cosA
= 52 + 102 – 2.5.10.cos60°
= 75.
Suy ra BC = \(\sqrt {75} = 5\sqrt 3 \).
Diện tích ∆ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.5.10.\sin 60^\circ = \frac{{25\sqrt 3 }}{2}\) (đơn vị diện tích)
Ta có \(S = \frac{1}{2}BC.{h_a}\)
Suy ra \({h_a} = \frac{{2S}}{{BC}} = \frac{{2.25\sqrt 3 }}{{2.5\sqrt 3 }} = 5\).
Vậy ta chọn phương án C.
Câu 6:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
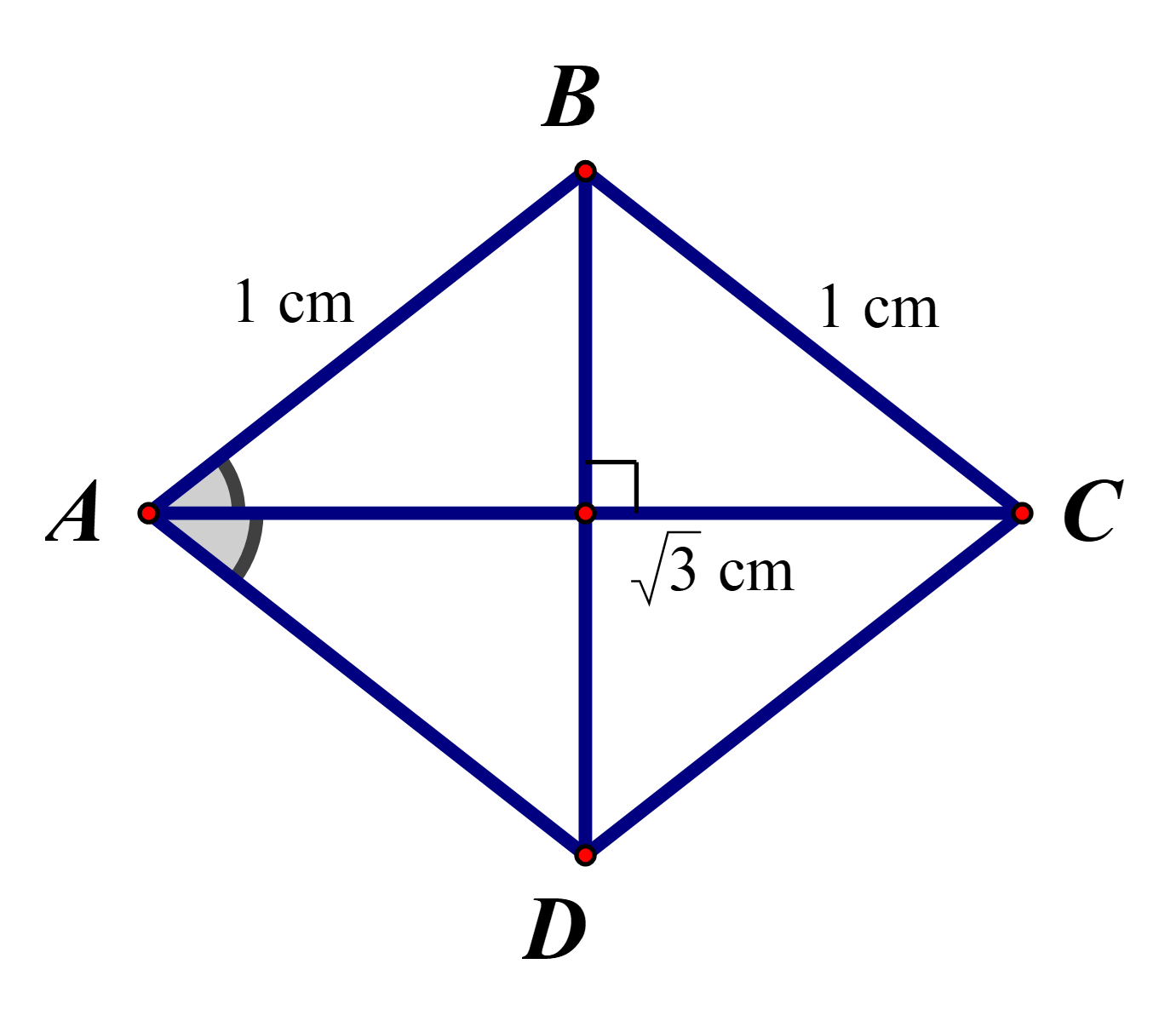
Vì ABCD là hình thoi có cạnh bằng 1 cm nên ta có AB = BC = 1 cm và AC = \(\sqrt 3 \) cm.
Áp dụng hệ quả của định lí côsin cho DABC, ta có:
\(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \frac{{{1^2} + {{\left( {\sqrt 3 } \right)}^2} - {1^2}}}{{2.1.\sqrt 3 }} = \frac{{\sqrt 3 }}{2}\).
Suy ra \(\widehat {BAC} = 30^\circ \).
Vì ABCD là hình thoi nên đường chéo AC là tia phân giác của \(\widehat {BAD}\).
Suy ra \(\widehat {BAD} = 2\widehat {BAC} = 2.30^\circ = 60^\circ \).
Vậy ta chọn phương án C.
Câu 7:
∆ABC có AB = 5, AC = 8 và \(\widehat {BAC} = 60^\circ \). Bán kính r của đường tròn nội tiếp ∆ABC bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Áp dụng định lí côsin cho DABC, ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
= 52 + 82 – 2.5.8.cos60°
= 49.
Suy ra BC = \(\sqrt {49} = 7\).
Diện tích ∆ABC là:
\(S = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.5.8.\sin 60^\circ = 10\sqrt 3 \) (đơn vị diện tích)
Nửa chu vi của ∆ABC là:
\(p = \frac{{AB + AC + BC}}{2} = \frac{{5 + 8 + 7}}{2} = 10\).
Ta có S = pr
\( \Leftrightarrow r = \frac{S}{p} = \frac{{10\sqrt 3 }}{{10}} = \sqrt 3 \).
Vậy bán kính r của đường tròn nội tiếp của ∆ABC bằng \(\sqrt 3 \).
Do đó ta chọn phương án C.
Câu 8:
Tam giác đều nội tiếp đường tròn bán kính R = 4 cm có diện tích bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Do ∆ABC đều nên \(\widehat {BAC} = 60^\circ \).
Áp dụng định lí sin cho ∆ABC, ta có \(\frac{{BC}}{{\sin \widehat {BAC}}} = 2R\)
⇔ BC = 2R.sinA = 2.4.sin60° = \(4\sqrt 3 \).
Vì ∆ABC đều nên ta có AB = AC = BC = \(4\sqrt 3 \).
Diện tích ∆ABC là:
\(S = \frac{{AB.AC.BC}}{{4R}} = \frac{{4\sqrt 3 .4\sqrt 3 .4\sqrt 3 }}{{4.4}} = 12\sqrt 3 \) (cm2)
Do đó ta chọn phương án C.