Hướng dẫn giải

Đáp án đúng là: B

Có tất cả 15 + 6 = 21 người trong hội nghị.

Chọn ngẫu nhiên 3 trong số 21 người và không tính đến thứ tự thì có $C_{21}^3=1330$  cách chọn.

Tức là n(Ω) = 1 330.

Gọi biến cố A: “3 người được chọn là nam”.

Chọn ngẫu nhiên 3 nam trong số 15 nam và không tính đến thứ tự thì có $C_{15}^3=455$  cách chọn.

Tức là n(A) = 455.

Vậy xác suất để 3 người được chọn là nam là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{455}{1330}=\frac{13}{38}$ .

Ta chọn phương án B.

Hướng dẫn giải

Đáp án đúng là: C

Số phần tử của không gian mẫu là: n(Ω) = 6.6 = 36.

Gọi biến cố A: “Hiệu số chấm các mặt xuất hiện của hai xúc xắc bằng 2”.

Suy ra tập hợp biến cố A là:

A = {(1; 3), (3; 1), (2; 4), (4; 2), (3; 5), (5; 3), (4; 6), (6; 4)}.

Do đó n(A) = 8.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{8}{36}=\frac{2}{9}$ .

Ta chọn phương án C.

Hướng dẫn giải

Đáp án đúng là: A

+) Gọi số tự nhiên gồm 4 chữ số khác nhau là $\overline{abcd}$ .

Có tất có 10 chữ số là {0; 1; 2; …; 9}.

• Chọn a có 9 cách chọn từ các chữ số trong {1; 2; …; 8; 9}.

• Chọn 3 chữ số còn lại trong 9 chữ số và xếp vào 3 vị trí b, c, d có $A_9^3$  cách.

Do đó chọn ngẫu nhiên một số tự nhiên có 4 chữ số khác nhau (có quan tâm đến thứ tự) thì có $9.A_9^3$  = 4 536 cách chọn.

Tức là ta có số phần tử của không gian mẫu n(Ω) = 4 536.

+) Số tự nhiên được chọn gồm 4 số 3; 4; 5; 6.

• Chọn a có 4 cách chọn từ các chữ số trong {3; 4; 5; 6}.

• Chọn b có 3 cách chọn một chữ số từ ba chữ số còn lại sau khi chọn a.

• Chọn c có 2 cách chọn một chữ số từ ba chữ số còn lại sau khi chọn a, b.

• Chọn d có 1 cách chọn một chữ số còn lại sau khi chọn a, b, c.

Số phần tử của A là: n(A) = 4.3.2 = 24.

Hoặc ta cũng có thể tính n(A) như sau:

Chọn 4 chữ số trong tập hợp các chữ số {3; 4; 5; 6} và xếp vào 4 vị trí a, b, c, d sẽ có 4! = 24 cách.

Xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{24}{4536}=\frac{1}{189}$ .

Vậy ta chọn phương án A.

Hướng dẫn giải

Đáp án đúng là: D

Gọi biến cố A: “Có ít nhất 2 lần lấy viên bi cùng màu ”.

Ta kí hiệu X, Đ, T lần lượt để chỉ các viên bi màu xanh, màu đỏ, màu trắng.

Các kết quả có thể xảy ra trong 3 lần lấy ngẫu nhiên một viên bi được thể hiện ở sơ đồ hình cây sau:

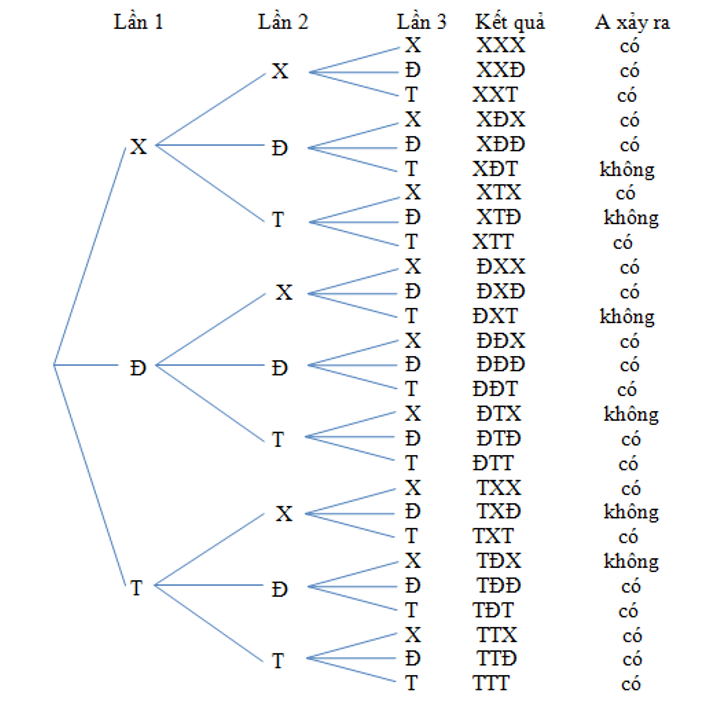
Quan sát sơ đồ hình cây, ta thấy có tổng cộng là 27 kết quả. Tức là, n(Ω) = 27.

Trong đó có 21 kết quả thuận lợi cho biến cố A. Tức là, n(A) = 21.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{21}{27}=\frac{3}{4}$ .

Ta chọn phương án D.

Hướng dẫn giải

Đáp án đúng là: C

Số phần tử của không gian mẫu là: n(Ω) = 5! = 120.

Gọi biến cố A: “Số tìm được không có dạng $\overline{135xy}$  ”.

Suy ra biến cố đối của biến cố A là:$\overline{A}$ : “Số tìm được có dạng $\overline{135xy}$ ”.

⦁ x có 2 cách chọn là x = 7 hoặc x = 9.

⦁ y có 1 cách chọn.

Theo quy tắc đếm, ta có $n\left(\overline{A}\right)$  = 1.1.1.2.1 = 2 cách chọn.

Vì vậy xác suất của biến cố $\overline{A}$  là: $P\left(\overline{A}\right)=\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{2}{120}=\frac{1}{60}$ .

Ta có $P\left(A\right)+P\left(\overline{A}\right)=1$ .

Suy ra $P\left(A\right)=1-P\left(\overline{A}\right)=1-\frac{1}{60}=\frac{59}{60}$ .

Vậy ta chọn phương án C.

Hướng dẫn giải

Đáp án đúng là: D

Chọn ngẫu nhiên 3 học sinh trong số 30 học sinh tham dự đại hội thì có $C_{30}^3=4060$  cách chọn. Do đó n(Ω) = 4060.

Gọi biến cố C: “Trong 3 học sinh được chọn không có học sinh trung bình”.

Tức là ta chỉ chọn ngẫu nhiên 3 học sinh là học sinh khá, giỏi.

Có tất cả 8 + 15 = 23 (học sinh khá, giỏi).

Vì vậy ta có n(C) = $C_{23}^3=1771$ .

Vậy xác suất của biến cố C là: $P\left(C\right)=\frac{n\left(C\right)}{n\left(\Omega \right)}=\frac{1771}{4060}=\frac{253}{580}$ .

Ta chọn phương án D.

Hướng dẫn giải

Đáp án đúng là: B

Lớp học có tất cả 20 + 15 = 35 học sinh.

Giáo viên chọn ngẫu nhiên 4 học sinh trong số 35 học sinh của lớp và không tính đến thứ tự thì có $C_{35}^4=52360$  cách chọn.

Tức là n(Ω) = 52 360.

Gọi biến cố H: “Trong 4 học sinh được chọn có cả nam và nữ”.

Khi đó biến cố đối của biến cố H là:$\overline{H}$ : “4 học sinh được chọn chỉ có nam hoặc chỉ có nữ”.

Số cách chọn ngẫu nhiên 4 học sinh nam và không tính đến thứ tự là:$C_{20}^4=4845$ .

Số cách chọn ngẫu nhiên 4 học sinh nữ và không tính đến thứ tự là: $C_{15}^4=1365$ .

Vì vậy n($\overline{H}$) = 4 845 + 1 365 = 6 210.

Khi đó xác suất của biến cố $\overline{H}$  là:$P\left(\overline{H}\right)=\frac{n\left(\overline{H}\right)}{n\left(\Omega \right)}=\frac{6210}{52360}=\frac{621}{5236}$ .

Ta có $P\left(H\right)+P\left(\overline{H}\right)=1$ .

Suy ra $P\left(H\right)=1-P\left(\overline{H}\right)=1-\frac{621}{5236}=\frac{4615}{5236}$  .

Vậy ta chọn phương án B.

Hướng dẫn giải

Đáp án đúng là: A

Một tổ có 9 học sinh được xếp thành hàng dọc.

Suy ra số phần tử của không gian mẫu là: n(Ω) = 9!.

Gọi biến cố A: “5 học sinh nam đứng kề nhau”.

• Xếp 5 học sinh nam đứng kề nhau thì sẽ có 5! cách xếp.

• Sau đó ta coi 5 học sinh nam là 1 “người A”, rồi xếp “người A” cùng với 4 bạn nữ kia, tức là xếp 5 người, ta lại có 5! cách xếp.

Vì vậy n(A) = 5!.5!.

Vậy xác suất của biến cố A là:$P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{5!.5!}{9!}=\frac{5}{126}$ .

Ta chọn phương án A.