Trắc nghiệm Toán 10 CTST Ôn tập chương 10 (Vận dụng) có đáp án
-
727 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Có năm đoạn thẳng có độ dài lần lượt là 1 cm, 3 cm, 5 cm, 7 cm và 9 cm. Chọn ngẫu nhiên ba đoạn thẳng trong số năm đoạn thẳng trên. Xác suất để ba đoạn thẳng được chọn lập thành một tam giác là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Chọn ngẫu nhiên ba đoạn thẳng trong số năm đoạn thẳng và không tính đến thứ tự thì có cách chọn.
Suy ra số phần tử của không gian mẫu là: n(Ω) = 10.
Gọi biến cố S: “Ba đoạn thẳng được chọn lập thành một tam giác”.
Theo bất đẳng thức tam giác, ta có trong một tam giác, tổng độ dài hai cạnh bất kì luôn lớn hơn độ dài cạnh còn lại.
Trong năm đoạn thẳng trên, ta thấy các đoạn thẳng sau lập thành một tam giác:
⦁ 3 cm; 5 cm và 7 cm;
⦁ 3 cm; 7 cm và 9 cm;
⦁ 5 cm; 7 cm và 9 cm.
Suy ra biến cố S có ba kết quả thuận lợi hay n(S) = 3.
Vậy xác suất của biến cố S là: .
Ta chọn phương án C.
Câu 2:
Một hộp quà đựng 16 dây buộc tóc cùng chất liệu, cùng kiểu dáng nhưng khác nhau về màu sắc. Trong hộp có 8 dây xanh, 5 dây đỏ, 3 dây vàng. Bạn Hoa được chọn ngẫu nhiên 6 dây từ hộp quà để làm phần thưởng cho mình. Xác suất để trong 6 dây bạn Hoa chọn có ít nhất 1 dây vàng và có không quá 4 dây đỏ là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Chọn ngẫu nhiên 6 dây trong số 16 dây và không tính đến thứ tự thì có cách chọn.
Suy ra số phần tử của không gian mẫu là: n(Ω) = 8 008.
Gọi A: “Trong 6 dây bạn Hoa chọn có ít nhất 1 dây vàng và có không quá 4 dây đỏ”.
Suy ra biến cố đối của biến cố A là : “Trong 6 dây bạn Hoa chọn không có dây vàng hoặc có hơn 4 dây đỏ”.
Các trường hợp của biến cố đối là:
⦁ Trường hợp 1: Không có dây vàng nào. Có 8 + 5 = 13 dây xanh và đỏ.
Khi đó Hoa có cách chọn 6 dây trong 13 dây đó.
⦁ Trường hợp 2: Có 1 dây vàng và 5 dây đỏ.
Khi đó Hoa có cách chọn 1 dây vàng (trong 3 dây vàng) và 5 dây đỏ (trong 5 dây đỏ).
⦁ Trường hợp 3: Có 1 dây xanh và 5 dây đỏ.
Khi đó ta có cách chọn 1 dây xanh (trong 8 dây xanh) và 5 dây đỏ (trong 5 dây đỏ).
Kết hợp cả 3 trường hợp, ta có:
Suy ra xác suất của biến cố là:
Ta có
Suy ra
Vậy ta chọn phương án A.
Câu 3:
Một hộp chứa 3 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 6 viên bi từ hộp. Xác suất để 6 viên bi được lấy ra có đủ cả 3 màu là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Có tất cả 3 + 5 + 6 = 14 viên bi.
Chọn ngẫu nhiên 6 viên bi trong số 14 viên bi trong hộp và không tính đến thứ tự thì có cách chọn.
Suy ra số phần tử của không gian mẫu là: n(Ω) = 3 003.
Gọi A: “6 viên bi được lấy ra có đủ cả 3 màu”.
Suy ra : “6 viên bi được lấy ra không có đủ 3 màu”.
Các trường hợp của biến cố là:
⦁ Trường hợp 1: Chọn ra 6 viên bi chỉ có một màu.
Suy ra chỉ chọn được cả 6 viên màu vàng.
Do đó ta có 1 cách chọn.
⦁ Trường hợp 2: Chọn 6 viên bi có hai màu xanh và đỏ. Có 3 + 5 = 8 viên bi màu xanh, đỏ.
Khi đó ta có cách chọn.
⦁ Trường hợp 3: Chọn 6 viên bi có hai màu xanh và vàng. Có 3 + 6 = 9 viên bi màu xanh, vàng.
Khi đó ta có cách chọn (ta trừ đi 1 tức là trừ đi trường hợp chọn được cả 6 viên bi đều màu vàng).
⦁ Trường hợp 4: Chọn 6 viên bi có hai màu đỏ và vàng. Có 5 + 6 = 11 viên bi màu đỏ, vàng.
Khi đó ta có cách chọn (ta trừ đi 1 tức là trừ đi trường hợp chọn được cả 6 viên bi đều màu vàng).
Suy ra số phần tử của biến cố là:
Khi đó xác suất của biến cố là:
Ta có
Suy ra
Vậy ta chọn phương án A.
Câu 4:
Trong một buổi liên hoan có 10 cặp nam nữ, trong đó có 4 cặp vợ chồng. Chọn ngẫu nhiên 3 người để biểu diễn một tiết mục văn nghệ. Xác suất để 3 người được chọn không có cặp vợ chồng nào là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Số cách chọn ngẫu nhiên 3 người trong số 20 người là: .
Suy ra n(Ω) = 1 140.
Gọi A: “Trong 3 người được chọn không có cặp vợ chồng nào”.
Suy ra : “Trong 3 người được chọn có 1 cặp vợ chồng”.
Chọn 1 cặp vợ chồng trong số 4 cặp vợ chồng có cách chọn.
Chọn thêm 1 người trong số 18 người còn lại có cách chọn.
Suy ra
Xác suất của biến cố là:
Ta có
Suy ra
Vậy ta chọn phương án D.
Câu 5:
Trong buổi sinh hoạt nhóm của lớp, tổ một có 12 học sinh gồm 4 học sinh nữ trong đó có Mai và 8 học sinh nam trong đó có Đức. Chia tổ thành 3 nhóm, mỗi nhóm gồm 4 học sinh và phải có ít nhất 1 học sinh nữ. Số kết quả thuận lợi cho biến cố A: “Mai và Đức cùng một nhóm” là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Xét biến cố A: “Mai và Đức cùng một nhóm”, ta mô tả các khả năng thuận lợi cho biến cố A như sau:
Trường hợp 1:
• Mai và Đức cùng với 1 bạn nam và 1 bạn nữ thành một nhóm nên có duy nhất 1 cách chọn Mai và Đức và có cách chọn 1 bạn nam (trong 7 bạn nam còn lại) và 1 bạn nữ (trong 3 bạn nữ còn lại).
• Nhóm thứ hai có 3 bạn nam (trong 6 bạn nam còn lại) và 1 bạn nữ (trong 2 bạn nữ còn lại) nên có cách.
• Cuối cùng còn lại 3 bạn nam và 1 bạn nữ nên có 1 cách duy nhất cho nhóm thứ ba.
Do đó trong trường hợp này có cách.
Trường hợp 2:
• Mai và Đức cùng với 2 bạn nam thành một nhóm nên có duy nhất 1 cách chọn Mai và Đức và có cách chọn 2 bạn nam trong 7 bạn nam còn lại.
• Nhóm thứ hai có 2 bạn nam (trong 5 bạn nam còn lại) và 1 bạn nữ (trong 3 bạn nữ còn lại) nên có cách.
• Cuối cùng còn lại 2 bạn nam và 2 bạn nữ nên có 1 cách duy nhất cho nhóm thứ ba.
Do đó trong trường hợp này có cách.
Trường hợp 3:
• Mai và Đức cùng với 2 bạn nam thành một nhóm.
• Nhóm thứ hai có 2 bạn nam và 2 bạn nữ.
• Suy ra nhóm thứ ba có 3 bạn nam và 1 bạn nữ.
Trường hợp này trùng với trường hợp thứ hai nên ta không tính.
Suy ra số kết quả thuận lợi cho biến cố A là 840 + 630 = 1 470.
Câu 6:
Xếp ngẫu nhiên 10 học sinh gồm 5 học sinh nam (trong đó có Bình) và 5 học sinh nữ (trong đó có Phương) thành một hàng ngang. Số kết quả thuận lợi cho biến cố A: “Trong 10 học sinh trên không có hai học sinh cùng giới đứng cạnh nhau, đồng thời Bình và Phương cũng không đứng cạnh nhau” là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Chọn vị trí chẵn hoặc lẻ để xếp 5 nam: có 2 cách.
Ta xét trường hợp 5 nam ở vị trí chẵn (tương tự cho vị trí lẻ):
• Khả năng 1: Bình đứng ngoài cùng: có 1 cách.
Xếp Phương không cạnh Bình: có 4 cách.
Đổi vị trí các bạn nam: có 4! cách;
Đổi vị trí các bạn nữ: 4! cách.
Do đó trong khả năng này có 2.1.4.4!.4! = 4 608 cách.
• Khả năng 2: Bình không đứng ngoài cùng: có 4 cách.
Xếp Phương không cạnh Bình (bỏ 2 vị trí cạnh Bình): có 3 cách.
Đổi vị trí các bạn nam: có 4! cách;
Đổi vị trí các bạn nữ: có 4! cách.
Do đó trong khả năng này có 2.4.3.4!4! = 13 824 cách.
Khi đó có 4 608 + 13 824 = 18 432 cách.
Vậy số kết quả thuận lợi cho biến cố A là 18 432.
Câu 7:
Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Xác suất để 1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có ai là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Không gian mẫu của phép thử trên là số cách xếp 4 hành khách lên 4 toa tàu.
Vì chọn mỗi hành khách có 4 cách chọn toa nên ta có 44 cách xếp.
Suy ra số phần tử của không gian mẫu là n(Ω) = 44.
Gọi biến cố A: “1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có ai”.
Để tìm số phần tử của biến cố A, ta chia thành hai giai đoạn như sau:
Giai đoạn 1: Chọn 3 hành khách trong số 4 hành khách và chọn 1 toa trong số 4 toa.
Sau đó xếp lên toa đó 3 hành khách vừa chọn.
Khi đó ta có cách.
Giai đoạn 2: Chọn 1 toa trong số 3 toa còn lại và xếp 1 hành khách còn lại lên toa đó.
Suy ra có cách. Hiển nhiên khi đó 2 toa còn lại sẽ không có hành khách nào.
Theo quy tắc nhân, ta có n(A) = .
Vậy xác suất của biến cố A là: .
Ta chọn phương án B.
Câu 8:
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có tọa độ các đỉnh A(–2; 0), B(–2; 2), C(4; 2), D(4; 0). Chọn ngẫu nhiên một điểm có tọa độ (x; y) (với x, y là các số nguyên) nằm trong hình chữ nhật ABCD, kể cả các điểm nằm trên cạnh. Gọi A là biến cố “x, y đều chia hết cho 2”. Xác suất của biến cố A là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
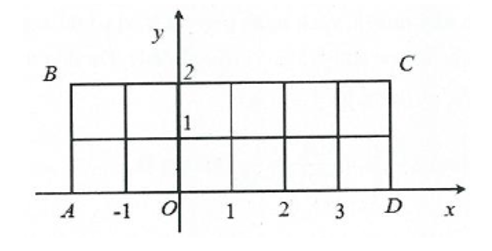
Ta có Ω = {(x; y) | x, y ∈ ℤ; –2 ≤ x ≤ 4 và 0 ≤ y ≤ 2}.
Khi đó x ∈ {–2; –1; 0; 1; 2; 3; 4} và y ∈ {0; 1; 2}.
Chọn 1 hoành độ có 7 cách chọn và chọn 1 tung độ có 3 cách chọn.
Áp dụng quy tắc nhân, ta suy ra n(Ω) = 7.3 = 21 (mỗi điểm là một giao điểm trên hình).
Ta có A: “x, y đều chia hết cho 2”.
Suy ra A = {(x; y) | x ∈ {–2; 0; 2; 4} và y ∈ {0; 2}}.
Chọn 1 hoành độ (chia hết cho 2) có 4 cách chọn và chọn 1 tung độ (chia hết cho 2) thì có 2 cách chọn.
Theo quy tắc nhân, ta có n(A) = 4.2 = 8.
Vậy xác suất của biến cố A là: .
Ta chọn phương án D.
Câu 9:
Gieo một con xúc xắc cân đối và đồng chất. Giả sử xúc xắc xuất hiện mặt b chấm. Xác suất để phương trình x2 + bx + 2 = 0 có hai nghiệm phân biệt là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Số phần tử của không gian mẫu là: n(Ω) = 6.
Gọi K: “Phương trình x2 + bx + 2 = 0 có hai nghiệm phân biệt”.
Ta có ∆ = b2 – 8.
Phương trình x2 + bx + 2 = 0 có hai nghiệm phân biệt khi và chỉ khi ∆ > 0
⇔ b2 – 8 > 0
Lại có xúc xắc xuất hiện mặt b chấm nên b ∈ {1; 2; 3; 4; 5; 6}.
Do đó ta nhận b ∈ {3; 4; 5; 6}.
Suy ra n(K) = 4.
Vậy xác suất của biến cố K là: .
Ta chọn phương án A.
Câu 10:
Gieo một con xúc xắc cân đối và đồng chất. Giả sử con xúc xắc xuất hiện mặt b chấm. Xác suất sao cho phương trình x2 – bx + b – 1 = 0 (x là ẩn số) có nghiệm lớn hơn 3 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Số phần tử của không gian mẫu là: n(Ω) = 6.
Gọi H: “Phương trình x2 – bx + b – 1 = 0 có nghiệm lớn hơn 3”.
Ta có xúc xắc xuất hiện mặt b chấm.
Suy ra b ∈ {1; 2; 3; 4; 5; 6}.
Xét phương trình x2 – bx + b – 1 = 0 (1)
∆ = (–b)2 – 4.1.(b – 1) = b2 – 4b + 4 = (b – 2)2 ≥ 0, với mọi b ∈ ℝ.
Suy ra phương trình đã cho có hai nghiệm x1, x2 là:
Theo đề, ta có phương trình đã cho có nghiệm lớn hơn 3.
Mà x2 = 1 < 3
Suy ra x1 > 3
⇔ b – 1 > 3
⇔ b > 4.
Mà b ∈ {1; 2; 3; 4; 5; 6} và 2 ≤ b ≤ 6.
Suy ra ta nhận b = 5 và b = 6.
Khi đó số phần tử của tập hợp mô tả biến cố H là: n(H) = 2.
Xác suất của biến cố H là: .
Vậy ta chọn phương án A.
