Trắc nghiệm Toán 10 Ôn tập chương 1 (Thông hiểu ) có đáp án
-
613 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Mệnh đề phủ định của mệnh đề P: “5x – 4 ≤ 0” là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Mệnh đề phủ định của mệnh đề P là “Không phải P”, kí hiệu là \(\overline P \).
Phủ định của “≤” là “>”.
Vậy mệnh đề phủ định của P là \(\overline P \) : “5x – 4 > 0”.
Câu 2:
Liệt kê các phần tử của tập hợp E = {x ∈ ℝ| 2x2 – 3x + 1 = 0}:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Các phần tử của tập hợp E là các nghiệm thực của phương trình 2x2 – 3x + 1 = 0.
Giải phương trình 2x2 – 3x + 1 = 0 ta được các nghiệm là x = 1, x = \(\frac{1}{2}\).
Vì 1; \(\frac{1}{2}\) đều là các số thực.
Do đó, cả hai số đều là phần tử của tập hợp E.
Ta viết \(E = \left\{ {\frac{1}{2};\;1} \right\}\).
Câu 3:
Cho mệnh đề: “Nếu hai góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Trong mệnh đề: “Nếu hai góc ở vị trí so le trong thì hai góc đó bằng nhau”, ta thấy:
⦁ P: “Hai góc ở vị trí so le trong”;
⦁ Q: “Hai góc đó bằng nhau”.
Mệnh đề P ⇒ Q có mệnh đề đảo là mệnh đề Q ⇒ P.
Mệnh đề Q ⇒ P được phát biểu như sau: “Nếu hai góc bằng nhau thì hai góc đó ở vị trí
so le trong”.
Vậy ta chọn phương án A.
Câu 4:
Mệnh đề nào dưới đây đúng ?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
+ Mệnh đề A là mệnh đề sai vì nếu ta lấy hai số tự nhiên là 3 và 4 thì ta có 3 + 4 = 7 ⁝ 7 nhưng 3 và 4 không chia hết cho 7.
+ Mệnh đề B là mệnh đề đúng vì tổng của hai số hữu tỉ là một số hữu tỉ.
+ Mệnh đề C là mệnh đề sai vì nếu ta lấy hai số tự nhiên là 3 và 12 đều không chia hết cho 9 nhưng 3 . 12 = 36 chia hết cho 9.
+ Mệnh đề D là mệnh đề sai vì nếu ta lấy hai số vô tỉ là \(\sqrt 3 \) và \(2\sqrt 3 \) thì tích của chúng là \(\sqrt 3 .2\sqrt 3 = 2.3 = 6\) là một số hữu tỉ.
Câu 5:
Cho tập hợp P = {1; 3} và tập hợp Q = {3; x}. Giá trị của x để P = Q là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta thấy tập hợp P và Q đều có phần tử 3.
Tập P còn có phần tử 1.
Do đó để P = Q thì Q cần có thêm phần tử 1.
Nghĩa là, x = 1.
Vậy ta chọn phương án A.
Câu 6:
Cho tập hợp A = (– ∞; – 2] và tập B = (– 1; + ∞). Khi đó A ∪ B là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Để xác định tập hợp A ∪ B, ta vẽ sơ đồ sau đây:
![Cho tập hợp A = (– vô cùng; – 2] và tập B = (– 1; + vô cùng). Khi đó A hợp B là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/08/blobid0-1661391575.png)
Từ sơ đồ, ta thấy A ∪ B = ℝ.
Vậy ta chọn phương án C.
Câu 7:
Cho bốn tập hợp E, F, G, K thỏa mãn E ⊂ F, F ⊂ G và G ⊂ K. Khẳng định nào sau đây đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
⦁ F ⊂ G nên phương án A sai.
⦁ G ⊂ K nên phương án B sai.
⦁ Giả sử E = {1; 2}, F = {1; 2; 3}, G = {1; 2; 3; 4}.
Ta thấy trong trường hợp trên, ta có E ⊂ F, F ⊂ G nhưng F ⊄ E vì 3 ∈ F nhưng 3 ∉ E.
Do đó phương án C không đúng trong mọi trường hợp.
⦁ Ta có quan hệ bao hàm: E ⊂ F, F ⊂ G và G ⊂ K.
Ta biểu diễn mối quan hệ giữa bốn tập hợp trên biểu đồ Ven như hình bên:
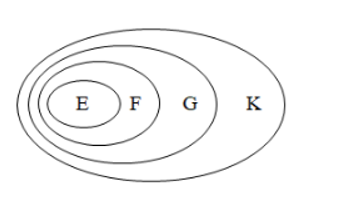
Quan sát biểu đồ Ven, ta thấy E ⊂ K.
Do đó phương án D đúng.
Câu 8:
Cho hai tập hợp A = {x ∈ ℤ| (x2 – 10x + 21)(x3 – x) = 0}, B = {x ∈ ℤ| – 3 < 2x + 1 < 5}. Khi đó tập X = A \ B là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
+ Giải phương trình (x2 – 10x + 21)(x3 – x) = 0 ⇔\[\left[ {\begin{array}{*{20}{c}}{{x^2} - 10x + 21 = 0}\\{{x^3} - x = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left[ {\begin{array}{*{20}{c}}{x = 3}\\{x = 7}\end{array}} \right.}\\{\left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \pm 1}\end{array}} \right.}\end{array}} \right.\].
Mà x ∈ ℤ nên A = {– 1; 0; 1; 3; 7}.
+ Giải bất phương trình – 3 < 2x + 1 < 5 ⇔ – 2 < x < 2. Mà x ∈ ℤ nên B = {– 1; 0; 1}.
Khi đó X = A \ B = {x| x ∈ A, x ∉ B} = {3; 7}.