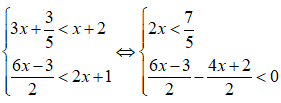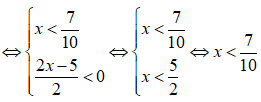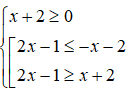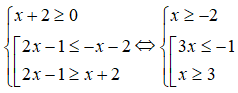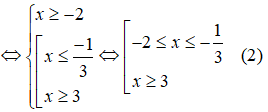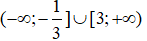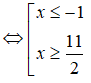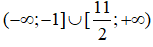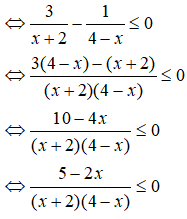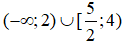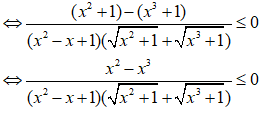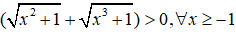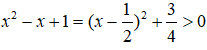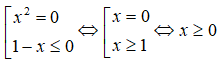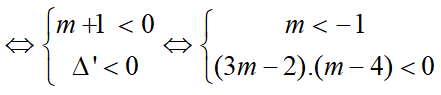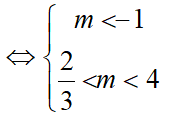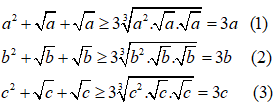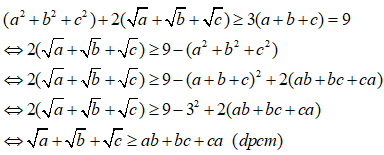11 câu hỏi trắc nghiệm thuộc Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 3)

Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 1)

Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 3)

1296 lượt thi
11 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Phần I: Trắc nghiệm

Cho bảng xét dấu:

Hỏi bảng xét dấu trên của tam thức nào sau đây:

A. f(x) = - $x^{2}$ + 5x - 6

B. f(x) = $x^{2}$ - 5x + 6

C. f(x) = $x^{2}$ + 5x - 6

D. f(x) = - $x^{2}$ + 5x + 6

Xem đáp án

Đáp án A.

Dựa vào bảng xét dấu ta thấy phương trình f(x) = 0 có hai nghiệm là 2 và 3. Từ đó, ta loại được đáp án C và D.

Từ bảng xét dấu ta suy ra được hệ số a của tam thức bậc hai f(x) mang dấu âm

Câu 2:

Cho tam thức bậc hai f(x) = a $x^{2}$ + bx + c, (a ≠ 0) có biệt thức Δ = $b^{2}$ - 4ac. Chọn khẳng định đúng:

A. Nếu Δ < 0 thì af(x) > 0, ∀x ∈ R

B. Nếu Δ > 0 thì af(x) < 0, ∀x ∈ R

C. Nếu Δ ≤ 0 thì af(x) ≥ 0, ∀x ∈ R

D. Nếu Δ ≥ 0 thì af(x) > 0, ∀x ∈ R

Xem đáp án

Đáp án A.

Ta có: nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a với mọi giá trị của x, tức là af(x) > 0, ∀x ∈ R

Câu 3:

Tìm m để phương trình $x^{2}$ - 2x + m = 0 có hai nghiệm phân biệt

A. m < 4

B. m > 4

C. m < 1

D. m > 1

Xem đáp án

Đáp án C.

$x^{2}$ - 2x + m = 0

Δ' = (-1 $)^{2}$ - 1.m = 1 - m

Để phương trình có hai nghiệm phân biệt thì:

Δ' > 0 ⇔ 1 - m > 0 ⇔ m < 1

Câu 4:

Tập nghiệm của bất phương trình $x^{2}$ + 3x - 4 > 0 là:

A. ( $- \infty$ ;-4) ∪ (1; $+ \infty$ )

B. [-4;1]

C. (-4;1)

D. ( $- \infty$ ;-4] ∪ [1; $+ \infty$ )

Xem đáp án

Đáp án A.

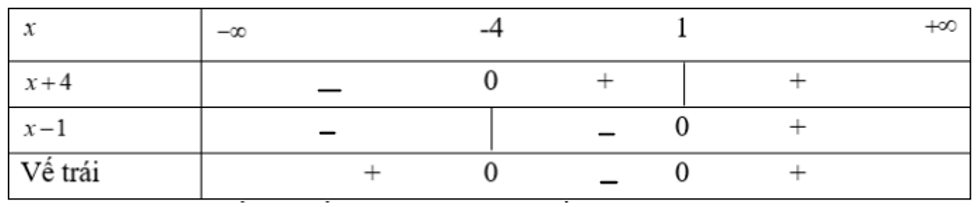
Ta có: $x^{2}$ + 3x - 4 > 0 ⇔ (x - 1)(x + 4) > 0

Ta có bảng xét dấu vế trái của bất phương trình là:

Dựa vào bảng xét dấu ta thấy, tập nghiệm của bất phương trình là: ( $- \infty$ ;-4) ∪ (1; $+ \infty$ )

Câu 5:

Hệ bất phương trình sau có nghiệm là:

$\{\begin{cases} 3 x + \frac{3}{5} < x + 2 \\ \frac{6 x - 3}{2} < 2 x + 1 \end{cases}$

A.x< $\frac{5}{2}$

B.x< $\frac{7}{10}$

C. $\frac{7}{10}$ <x< $\frac{5}{2}$

D.vô nghiệm

Xem đáp án

Đáp án: B

Ta có:

Câu 6:

Bất phương trình nào sau đây tương đương với bất phương trình x + 5 ≥ 0?

A. $- x^{2} (x + 5) \geq 0$

B. ${(x - 1)}^{2} (x + 5) \geq 0$

C. $\sqrt{x - 1} (x + 5) \geq 0$

D. ${(x + 5)}^{2} \geq 0$

Xem đáp án

Đáp án B.

Ta thấy bất phương trình ở đề bài và bất phương trình (x - 1 $)^{2}$ (x + 5) ≥ 0 cùng có tập nghiệm là: [-5; $+ \infty$ ). Do đó, hai bất phương trình này tương đương với nhau

Câu 7:

Tập xác định của hàm số sau là:

$y = \frac{2 x - 1}{\sqrt{- x^{2} - 4 x + 5}}$

A. D = [-5;1]

B. D = [-5;1)

C. D = (-5;1]

D. D = (-5;1)

Xem đáp án

Đáp án D.

Hàm số $y = \frac{2 x - 1}{\sqrt{- x^{2} - 4 x + 5}}$ xác định khi và chỉ khi - $x^{2}$ - 4x + 5 > 0 ⇔ -5 < x < 1

Câu 8:

Tập nghiệm của bất phương trình |2x - 1| > x + 2 là:

A. $[- 2; - \frac{1}{3}] \cup [3; + \infty)$

B. $[- \infty; - \frac{1}{3}] \cup [3; + \infty)$

C. $(- \infty; - 2]$

D. $[3; + \infty)$

Xem đáp án

Đáp án B.

Ta có:

|2x - 1| ≥ x + 2 ⇔ x + 2 < 0

hoặc

• x + 2 < 0 ⇔ x < -2 (1)

•

Kết hợp (1) và (2) ta có nghiệm của bất phương trình là:

Câu 9:

Phần II: Tự luận

Giải các bất phương trình sau:

a) $- 2 {(x - 1)}^{2} + 5 (x + 3) \leq 2$

b) $\frac{3}{x + 2} \leq \frac{1}{4 - x}$

c) $\frac{\sqrt{x^{2} + 1} - \sqrt{x^{3} + 1}}{x^{2} - x + 1} \leq 0$

Xem đáp án

a) -2(x - 1 $)^{2}$ + 5(x + 3) ≤ 2

⇔-2( $x^{2}$ - 2x + 1) + 5x + 15 ≤ 2

⇔-2 $x^{2}$ + 4x - 2 + 5x + 15 - 2 ≤ 0

⇔-2 $x^{2}$ + 9x + 11 < 0

⇔-(x + 1)(2x - 11) < 0

Vậy tập nghiệm của bất phương trình là:

b) $\frac{3}{x + 2} \leq \frac{1}{4 - x}$

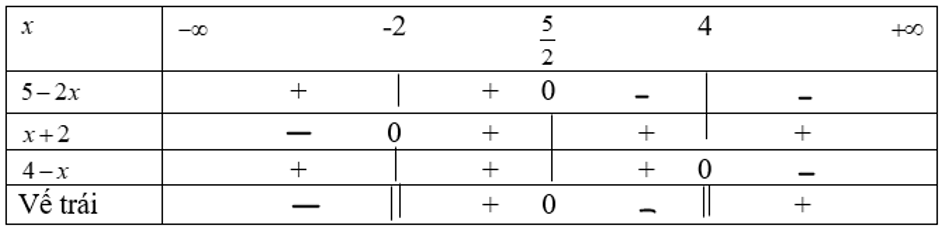
Ta có bảng xét dấu vế trái của bất phương trình:

Từ bảng xét dấu trên ta thấy, tập nghiệm của bất phương trình là:

c) $\frac{\sqrt{x^{2} + 1} - \sqrt{x^{3} + 1}}{x^{2} - x + 1} \leq 0$

ĐKXĐ: x ≥ -1

Vì

và

∀x nên bất phương trình tương đương:

$x^{2}$ - $x^{3}$ ≤ 0 ⇔ $x^{2}$ (1 - x) ≤ 0(*)

Vì $x^{2}$ ≥ 0 nên bất phương trình (*) tương đương:

Vậy tập nghiệm của bất phương trình là: [0; $+ \infty$ )

Câu 10:

Tìm các giá trị của m để bất phương trình sau vô nghiệm:

f(x) = (m + 1) $x^{2}$ - 2(3 - 2m)x + m + 1 ≥ 0

Xem đáp án

f(x) = (m + 1) $x^{2}$ - 2(3 - 2m)x + m + 1 ≥ 0 (1)

Với m = -1:

(1) ⇔ -10x ≥ 0 ⇔ x ≤ 0

Vậy với m = -1 bất phương trình (1) có nghiệm x ≤ 0

Suy ra, m = -1 (loại)

Với m ≠ -1:

f(x) = (m +1 ) $x^{2}$ - 2(3 - 2m)x + m + 1

Δ' = [-(3 - 2m) $]^{2}$ - (m + 1)(m + 1) = (2m - 3 $)^{2}$ - (m + 1 $)^{2}$

= (2m - 3 + m + 1)(2m - 3 - m - 1) = (3m - 2)(m - 4)

Để bất phương trình (1) vô nghiệm thì:

Vậy không có giá trị nào của m để bất phương trình (1) vô nghiệm

Câu 11:

Cho ba số a, b, c dương thỏa mãn a + b + c = 3. Chứng minh rằng: $\sqrt{a} + \sqrt{b} + \sqrt{c} \geq a b + a c + b c$

Xem đáp án

Áp dụng bất đẳng thức Cô – si ta có:

Cộng vế với vế bất phương trình (1), (2), (3) ta được:

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 1)

Đề kiểm tra 45 phút Đại số 10 Chương 4 có đáp án (Đề 3)

Danh sách câu hỏi

Phần I: Trắc nghiệm

Phần II: Tự luận

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương