Đề thi Giữa kì 1 Toán 10 có đáp án - Đề 2
-
1210 lượt thi
-
34 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trong các phát biểu sau, phát biểu nào không phải là mệnh đề?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Phát biểu “Bạn có thích học môn Toán không?” là một câu hỏi, không khẳng định tính đúng sai nên đây không phải mệnh đề.
Câu 2:
Trong các tập hợp sau, tập hợp nào là con của tập hợp A = {1; 2; 3; 4; 5}?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tập con của tập hợp A là tập hợp gồm các phần tử đều là phần tử của tập hợp A.
Tập A1 = {1; 6} không là tập con của tập A vì 6 ∉ A.
Tập A2 = {0; 1; 3} không là tập con của tập A vì 0 ∉ A.
Tập A3 = {4; 5} là tập con của tập A vì 4 ∈ A, 5 ∈ A.
Tập A4 = {0} không là tập con của tập A vì 0 ∉ A.
Vậy chỉ có tập A3 là tập con của tập A.
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: A = {x ∈ ℝ | – 5 ≤ x < 1} = [– 5; 1)
Và B = {x ∈ ℝ | – 3 < x ≤ 3} = (– 3; 3].
Do đó, A ∪ B = {x | x ∈ A hoặc x ∈ B} = [– 5; 3].
Câu 4:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Giả sử đường thẳng d có phương trình: y = ax + b.
Từ hình vẽ ta thấy, đường thẳng d đi qua hai điểm có tọa độ (0; 1) và (0,5; 0).
Khi đó ta có hệ =>.
Do đó, d: y = – 2x + 1 hay d: 2x + y = 1.
Lấy điểm O(0; 0) không thuộc đường thẳng d, ta thấy 2 . 0 + 0 = 0 < 1 và nửa mặt phẳng không bị gạch chéo không chứa điểm O.
Vậy nửa mặt phẳng không bị gạch chéo ở hình đã cho là miền nghiệm của bất phương trình 2x + y > 1.
Câu 5:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Thay lần lượt các cặp số vào hệ bất phương trình ta thấy chỉ có cặp số (– 1; 1) không thỏa mãn, do cặp số này không thỏa mãn bất phương trình thứ hai của hệ (2 . (– 1) – 3 . 1 + 2 = – 3 < 0).
Vậy trong các cặp số đã cho, cặp số (– 1; 1) không là nghiệm của hệ bất phương trình đã cho.
Câu 6:
Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Hai góc bù nhau thì sin bằng nhau, côsin, tang và côtang đối nhau.
Do đó, sin (180° – α) = sin α; cos (180° – α) = – cos α;
tan (180° – α) = – tan α; cot (180° – α) = – cot α).
Vậy trong các đáp án đã cho, đáp án đúng là đáp án B.
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Áp dụng định lí côsin trong tam giác ABC ta có:
AB2 = BC2 + AC2 – 2 BC. AC . cosC = 12 + 32 – 2 . 1 . 3 . cos 60° = 7.
Suy ra AB = .
Câu 8:
Cho hai mệnh đề P: “x là số chẵn” và Q: “x chia hết cho 2”.
Phát biểu mệnh đề P kéo theo Q.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì mệnh đề kéo theo được phát biểu dưới dạng là “Nếu P thì Q”.
Nên mệnh đề P kéo theo Q là “Nếu x là số chẵn thì x chia hết cho 2”.
Câu 9:
Trong các cặp số sau đây: (– 5; 0); (– 2; 1); (– 1; 3); (– 7; 0). Có bao nhiêu cặp số là nghiệm của bất phương trình x – 4y + 5 ≥ 0?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
– 5 – 4.0 + 5 = 0, vậy (– 5; 0) là nghiệm của bất phương trình.
– 2 – 4.1 + 5 = – 1 < 0, vậy (– 2; 1) không là nghiệm của bất phương trình.
– 1 – 4.3 + 5 = – 8 < 0, vậy (– 1; 3) không là nghiệm của bất phương trình.
– 7 – 4.0 + 5 = – 2 < 0, vậy (–7; 0) không là nghiệm của bất phương trình.
Vậy có 1 cặp số là nghiệm của bất phương trình.
Câu 11:
Mệnh đề phủ định của mệnh đề P: “∃x, x2 + 2x + 3 là số chính phương” là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
Phủ định của ∃ là ∀.
Phủ định của “là số chính phương” là “không là số chính phương”.
Vậy mệnh đề phủ định ![]() của mệnh đề P là: “∀x, x2 + 2x + 3 không là số chính phương”.
của mệnh đề P là: “∀x, x2 + 2x + 3 không là số chính phương”.
Câu 12:
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét bất phương trình 2x2 + 1 ≥ y + 2x2 ⇔ 2x2 + 1 – 2x2 – y ≥ 0 ⇔ 0x – y ≥ – 1 (1)
Bất phương trình (1) có hai ẩn x, y có lũy thừa bậc cao nhất là bậc một và các hệ số a = 0, b = –1, c = – 1.
Do đó, đây là một bất phương trình bậc nhất hai ẩn.
Chú ý: Đáp án B không thỏa mãn vì ta biến đổi đưa về được 5 < 3 (vô lí).
Đáp án C, D bậc của các ẩn không phải bậc nhất.
Câu 13:
Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. Khẳng định nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Định lí côsin:
Trong tam giác ABC: a2 = b2 + c2 – 2bccosA.
Vậy đáp án đúng là B.
Câu 14:
Cho tập hợp D = {x ∈ ℕ* | x(x – 2)(x – 3) = 0}.
Viết lại tập hợp D dưới dạng liệt kê các phần tử của tập hợp đó
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: x(x – 2)(x – 3) = 0
Vì x ∈ ℕ* nên ta loại nghiệm x = 0.
Do đó tập hợp D gồm 2 phần tử là 2 và 3.
Vậy D = {2; 3}.
Câu 15:
Hệ nào là hệ bất phương trình bậc nhất hai ẩn trong các hệ sau?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Câu 16:
Cho tam giác ABC với độ dài 3 cạnh BC, AC, AB lần lượt là a, b, c. S là diện tích và p là nửa chu vi tam giác. R là bán kính đường tròn ngoại tiếp và r là bán kính đường tròn nội tiếp tam giác. Công thức nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Câu 17:
Cho , chọn đáp án SAI trong các đáp án dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có sin A = sin 45° = , suy ra đáp án sai là A.
cos A = cos 45° =
tan A = tan 45° = 1;
cot A = cot 45° = 1.
Vậy các đáp án B, C, D đúng.
Câu 18:
Cho tam giác ABC có BC = a, AC = b, AB = c, có R, r lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và hc là độ dài đường cao xuất phát từ đỉnh C. Chọn mệnh đề sai.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Các công thức tính diện tích tam giác ABC:
SABC = =absinC==pr
Do đó, đáp án A sai.
Câu 19:
Cho hệ bất phương trình. Trong các điểm sau đây, điểm không thuộc miền nghiệm của hệ bất phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
+ Lần lượt thay các cặp số (0; 0), (2; 3), (5; 4) vào các bất phương trình của hệ đã cho, ta thấy đều thỏa mãn, do đó (0; 0), (2; 3), (5; 4) là các nghiệm của hệ đã cho.
Vậy các điểm O, A, B thuộc miền nghiệm của hệ bất phương trình
+ Thay cặp số (−2 ; −2) vào bất phương trình thứ nhất của hệ ta được:
7 . (−2) − 5 . (−2) + 2 ≥ 0 là mệnh đề sai (do 7 . (−2) − 5 . (−2) + 2 = – 2 < 0).
Do đó (−2 ; −2) không là nghiệm của bất phương trình thứ nhất của hệ nên nó không là nghiệm của hệ bất phương trình trên.
Vậy điểm C(−2 ; −2) không thuộc miền nghiệm của hệ bất phương trình trên.
Câu 21:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Mệnh đề P ⇒ Q đúng thì ta nói P là điều kiện đủ để có Q.
Do đó, ta phát biểu mệnh đề “nếu a + b < 2 thì một trong hai số a và b nhỏ hơn 1” bằng cách sử dụng khái niệm “điều kiện đủ” như sau: “a + b < 2 là điều kiện đủ để một trong hai số a và b nhỏ hơn 1”.
Câu 22:
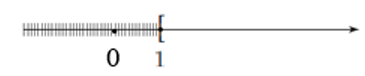
Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Quan sát hình vẽ ta thấy phần không bị gạch là phần phía bên phải của điểm 1 trên trục số, bao gồm cả điểm 1 (do có dấu “[”), do đó phần không bị gạch biểu diễn các số thực x sao cho x ≥ 1, do đó phần không bị gạch trên hình vẽ minh họa cho tập hợp [1; + ∞).
Câu 23:
Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Áp dụng mối liên hệ hai góc bù nhau, ta có:
sin α = sin β; cos α = – cos β; tan α = – tan β; cot α = – cot β.
Vậy đáp án A, B, C đúng và đáp án D sai.
Câu 24:
Cho hai tập hợp A = {1; 2; 4; 6} và B = {1; 2; 3; 4; 5; 6; 7; 8}. Xác định tập CBA.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: CBA = B \ A = {x| x ∈ B, x ∉ A} = {3; 5; 7; 8}.
Các phần tử thuộc tập B nhưng không thuộc tập A là: 3; 5; 7; 8.
Vậy CBA = {3; 5; 7; 8}.
Câu 25:
Miền nghiệm của bất phương trình x + y ≤ 2 là phần tô đậm của hình vẽ nào, trong các hình vẽ sau (kể cả bờ)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Biểu diễn miền nghiệm của bất phương trình x + y ≤ 2 như sau:
+) Vẽ đường thẳng x + y = 2 đi qua 2 điểm (2; 0) và (0; 2) trên mặt phẳng tọa độ.
+) Lấy điểm O(0; 0) không thuộc đường thẳng x + y = 2.
+) Ta có: 0 + 0 = 0 < 2.
Vậy miền nghiệm của bất phương trình x + y ≤ 2 là nửa mặt phẳng bờ là đường thẳng x + y = 2 chứa điểm O (là phần tô đậm ở đáp án A).
Câu 26:
Tam giác ABC có AB = 4, BC = 6, AC = . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
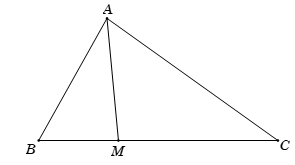
Theo hệ quả của định lí côsin trong tam giác ABC, ta có:
cosB = = = ![]() .
.
Do MC = 2MB Þ MB = BC = . 6 = 2.
Theo định lí côsin trong tam giác AMB, ta có:
AM2 = AB2 + BM2 – 2.AB.BM.cosB = 42 + 22 – 2.4.2.![]() = 12
= 12
Þ AM = 2.
Câu 27:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: sin α + cos α = 1
⇒ (sin α + cos α)2 = 12
⇔ sin2 α + 2 sin α . cos α + cos2 α = 1
Mà sin2 α + cos2 α = 1. Do đó, sin α . cos α = 0.
Từ đó suy ra sin α = 0 hoặc cos α = 0.
Lại có 0° < α < 180°, do đó sin α ≠ 0.
Vậy cos α = 0. Khi đó không tồn tại tan α.
Câu 28:
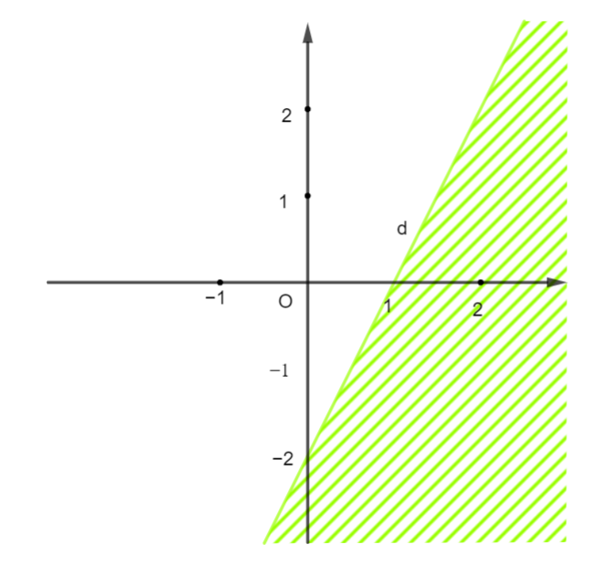
Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ bên (kể cả đường thẳng d)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi phương trình đường thẳng d có dạng: y = ax + b.
Đường thẳng d đi qua điểm (1; 0) và (0; −2) nên ta có hệ phương trình:
⇔
Vậy d: y = 2x − 2 hay d: 2x − y − 2 = 0.
Thay tọa độ điểm (0 ; 1) thuộc miền nghiệm (miền không bị gạch) vào biểu thức 2x – y – 2 ta được: 2 . 0 − 1 − 2 = −3 < 0.
Vậy miền nghiệm được biểu diễn bởi nửa mặt phẳng không bị gạch (kể cả đường thẳng d) là miền nghiệm của bất phương trình 2x − y − 2 ≤ 0 hay 2x − y ≤ 2.
Câu 31:
Cho bất phương trình 2x − 3y < 12 (với x, y Î ℝ). Điều nào sau đây là sai ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
+ Bất phương trình 2x – 3y < 12 có dạng ax + by < c nên đây là bất phương trình bậc nhất hai ẩn. Do đó, đáp án A đúng.
+ Thay cặp số (5; 3) vào bất phương trình 2x − 3y < 12 ta được:
2 . 5 − 3 . 3 < 12 ⇔ 1 < 12 (luôn đúng)
Vậy cặp số (5; 3) là nghiệm của bất phương trình.
Do đó, đáp án B đúng.
+ Thay cặp số (9; 2) vào bất phương trình 2x − 3y < 12 ta được:
2 . 9 − 3 . 2 < 12 ⇔ 12 < 12 (vô lí)
Vậy cặp số (9; 2) không là nghiệm của bất phương trình.
Do đó, đáp án C là sai.
+ Thay cặp (9; 3) vào bất phương trình 2x − 3y < 12 ta được:
2 . 9 − 3 . 3 < 12 ⇔ 9 < 12 (luôn đúng)
Vậy cặp số (9; 3) là nghiệm của bất phương trình.
Do đó, đáp án D đúng.
Câu 32:
Một công ty nhập về 1 tấn gỗ để sản xuất bàn và ghế. Biết một cái bàn cần 30 kg gỗ và một cái ghế cần 15 kg gỗ. Gọi x và y lần lượt là số bàn và số ghế mà công ty sản xuất. Viết bất phương trình bậc nhất hai ẩn x, y sao cho lượng bàn ghế mà công ty sản xuất không vượt quá 1 tấn gỗ ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đổi 1 tấn = 1 000 kg
Số gỗ để sản xuất x bàn là 30x (kg).
Số gỗ để sản xuất y ghế là 15y (kg)
Số gỗ để sản xuất x bàn và y ghế là 30x + 15y (kg)
Vì lượng bàn ghế mà công ty sản xuất không được vượt quá 1 tấn gỗ nên
30x + 15y ≤ 1 000.
Câu 33:
 Xem đáp án
Xem đáp án
Ta có: |x| ≤ 3 ⇔ – 3 ≤ x ≤ 3.
Do đó, A = {x ∈ ℝ | |x| ≤ 3} = {x ∈ ℝ | – 3 ≤ x ≤ 3} = [– 3; 3].
B = {x ∈ ℝ | – 2 < x ≤ 5} = (– 2; 5].
b) A ∪ B = [– 3; 3] ∪ (– 2; 5] = [– 3; 5]
A ∩ B = [– 3; 3] ∩ (– 2; 5] = (– 2; 3]
A \ B = [– 3; 3] \ (– 2; 5] = [– 3; – 2]
B \ A = (– 2; 5] \ [– 3; 3] = (3; 5].
Câu 34:
 Xem đáp án
Xem đáp án
A ∪ B = [– 3; 3] ∪ (– 2; 5] = [– 3; 5]
A ∩ B = [– 3; 3] ∩ (– 2; 5] = (– 2; 3]
A \ B = [– 3; 3] \ (– 2; 5] = [– 3; – 2]
B \ A = (– 2; 5] \ [– 3; 3] = (3; 5].

