15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Hệ trục tọa độ có đáp án (Vận dụng)

Câu 1:

Trong hệ tọa độ Oxy, cho tam giác ABC có M (2; 3), N (0; −4), P (−1; 6) lần lượt là trung điểm của các cạnh BC, CA, AB. Tìm tọa độ đỉnh A?

A. A(1;5).

B. A(−3;−1).

C. A(−2;−7).

D. A(1;−10).

Xem đáp án

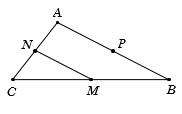
Gọi A (x; y)

Từ giả thiết, ta suy ra $\vec{P A} = \vec{M N}$ (*)

Ta có $\vec{P A} = (x + 1; y - 6)$ và $\vec{M N} = (- 2; - 7)$

Khi đó (*) $\Leftrightarrow \{\begin{matrix} x + 1 = - 2 \\ y - 6 = - 7 \end{matrix} \Leftrightarrow \{\begin{matrix} x = - 3 \\ y = - 1 \end{matrix} \Rightarrow A (- 3; - 1)$

Đáp án cần chọn là: B

Câu 2:

Trong mặt phẳng tọa độ Oxy cho $\vec{a} = (2; 1), \vec{b} = (3; 4), \vec{c} = (7; 2)$ . Cho biết $\vec{c} = m . \vec{a} + n . \vec{b}$ . Khi đó:

A. $m = - \frac{22}{5}; n = \frac{- 3}{5}$

B. $m = \frac{1}{5}; n = \frac{- 3}{5}$

C. $m = \frac{22}{5}; n = \frac{- 3}{5}$

D. $m = - \frac{22}{5}; n = \frac{3}{5}$

Xem đáp án

Ta có: $\vec{c} = m . \vec{a} + n . \vec{b}$ $\Leftrightarrow \{\begin{matrix} 7 = 2 m + 3 n \\ 2 = m + 4 n \end{matrix} \Leftrightarrow \{\begin{matrix} m = \frac{22}{5} \\ n = - \frac{3}{5} \end{matrix}$

Đáp án cần chọn là: C

Câu 3:

Cho ba vec tơ $\vec{a} = (2; 1), \vec{b} = (3; 4), \vec{c} = (7; 2)$ . Giả sử có các số k, h để $\vec{c} = k . \vec{a} + h . \vec{b}$ . Khi đó k – h có giá trị là:

A. 3,8

B. 9,7

C. 5

D. – 3,8

Xem đáp án

Ta có:

$\begin{matrix} k . \vec{a} = (2 k; k) \\ h . \vec{b} = (3 h; 4 h) \end{matrix}\} \Rightarrow k . \vec{a} + h . \vec{b} = (2 k + 3 h; k + 4 h)$

Theo đề bài:

$\Leftrightarrow \{\begin{matrix} 7 = 2 k + 3 h \\ 2 = k + 4 h \end{matrix} \Leftrightarrow \{\begin{matrix} k = 4, 4 \\ h = - 0, 6 \end{matrix} \Rightarrow k - h = 5$

Đáp án cần chọn là: C

Câu 4:

Cho các vec tơ $\vec{a} = (4; - 2), \vec{b} = (- 1; - 1), \vec{c} = (2; 5)$ . Phân tích vec tơ $\vec{b}$ theo hai vec tơ $\vec{a}$ và $\vec{c}$ , ta được:

A. $\vec{b} = - \frac{1}{8} \vec{a} - \frac{1}{4} \vec{c}$

B. $\vec{b} = \frac{1}{8} \vec{a} - \frac{1}{4} \vec{c}$

C. $\vec{b} = - \frac{1}{2} \vec{a} - 4 \vec{c}$

D. $\vec{b} = - \frac{1}{8} \vec{a} + \frac{1}{4} \vec{c}$

Xem đáp án

Giả sử $\vec{b} = m \vec{a} + n \vec{c} \Leftrightarrow \{\begin{matrix} - 1 = 4 m + 2 n \\ - 1 = - 2 m + 5 n \end{matrix} \Leftrightarrow \{\begin{matrix} m = - \frac{1}{8} \\ n = - \frac{1}{4} \end{matrix}$

Vậy $\vec{b} = - \frac{1}{8} \vec{a} - \frac{1}{4} \vec{c}$

Đáp án cần chọn là: A

Câu 5:

Trong mặt phẳng Oxy, cho A (m − 1; −1), B (2; 2 − 2m), C (m + 3; 3). Tìm giá trị m để A, B, C là ba điểm thẳng hàng?

A. m = 2.

B. m = 0.

C. m = 3.

D. m = 1.

Xem đáp án

Ta có: $\vec{A B} = (3 - m; 3 - 2 m), \vec{A C} = (4; 4)$

Ba điểm A, B, C thẳng hàng khi và chỉ khi $\vec{A B}$ cùng phương với $\vec{A C}$

$\Leftrightarrow \frac{3 - m}{4} = \frac{3 - 2 m}{4} \Leftrightarrow m = 0$

Đáp án cần chọn là: B

Câu 6:

Trong hệ tọa độ Oxy, cho hai điểm A (2; −3), B (3; −4). Tìm tọa độ điểm M trên trục hoành sao cho chu vi tam giác AMB nhỏ nhất.

A. M ( $\frac{18}{7}$ ; 0).

B. M (4; 0).

C. M (3; 0).

D. M( $\frac{17}{7}$ ; 0).

Xem đáp án

Cách 1: Do M trên trục hoành $\Rightarrow M (x; 0), \vec{A B} = (1; - 1) \Rightarrow A B = \sqrt{2}$

$\vec{A M} = (x - 2; 3), \vec{B M} = (x - 3; 4)$

Ta có chu vi tam giác AMB:

$P_{A B M} = \sqrt{2} + \sqrt{{(x - 2)}^{2} + 3^{2}} + \sqrt{{(x - 3)}^{2} + 4^{2}}$

$\geq \sqrt{2} + \sqrt{{(x - 2 + 3 - x)}^{2} + {(3 + 4)}^{2}}$

$\Leftrightarrow P_{A B M} \geq 6 \sqrt{2}$

Dấu bằng xảy ra khi $\frac{x - 2}{3 - x} = \frac{3}{4} \Leftrightarrow x = \frac{17}{7} \Rightarrow$ M( $\frac{17}{7}$ ; 0)

Cách 2: Lấy đối xứng A qua Ox ta được $A' (2; 3)$ . Ta có

$M A + M B = M A' + M B \geq A' B$

Dấu bằng xảy ra khi M trùng với giao điểm của A’B với Ox

Đáp án cần chọn là: D

Câu 7:

Cho các điểm A (−2; 1), B (4; 0), C (2; 3). Tìm điểm M biết rằng $\vec{C M} + 3 \vec{A C} = 2 \vec{A B}$

A. M (2; −5).

B. M (5; −2).

C. M (−5; 2).

D. M (2; 5).

Xem đáp án

Gọi M (x_M; y_M). Ta có:

$\vec{C M} + 3 \vec{A C} = 2 \vec{A B}$ $\Leftrightarrow \{\begin{matrix} x_{M} - 2 + 3 (2 + 2) = 2 (4 + 2) \\ y_{M} - 3 + 3 (3 - 1) = 2 (0 - 1) \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x_{M} = 2 \\ y_{M} = - 5 \end{matrix} \Rightarrow M (2; - 5)$

Đáp án cần chọn là: A

Câu 8:

Trong mặt phẳng Oxy, cho tam giác MNP có M (1; −1), N (5; −3) và P là điểm thuộc trục Oy, trọng tâm G của tam giác MNP nằm trên trục Ox. Tọa độ điểm P là

A. (2; 4).

B. (0; 4).

C. (0; 2).

D. (2; 0).

Xem đáp án

P ∈ Oy ⇒ P (0; y).

G ∈ Ox ⇒ G (x; 0).

Điểm G là trọng tâm của tam giác MNP $\Leftrightarrow \{\begin{matrix} x = \frac{1 + 5 + 0}{3} \\ 0 = \frac{(- 1) + (- 3) + y}{3} \end{matrix}$

$\Leftrightarrow \{\begin{matrix} x = 2 \\ y = 4 \end{matrix}$

$\Rightarrow P (0; 4), G (2; 0)$

Đáp án cần chọn là: B

Câu 9:

Cho A (1; 2), B (−2; 6). Điểm M trên trục Oy sao cho ba điểm A, B, M thẳng hàng thì tọa độ điểm M là:

A. (0; $\frac{10}{3}$ )

B. (0; −10).

C. (0; 10).

D. (−10; 0).

Xem đáp án

Ta có: M trên trục Oy ⇒ M (0; y)

Ba điểm A, B, M thẳng hàng khi $\vec{A B}$ cùng phương với $\vec{A M}$

Ta có $\vec{A B} = (- 3; 4), \vec{A M} = (- 1; y - 2)$

Do đó, $\vec{A B}$ cùng phương với $\vec{A M}$

⇔ $\frac{- 1}{- 3} = \frac{y - 2}{4} \Rightarrow y = \frac{10}{3}$

Vậy $M (0; \frac{10}{3})$

Đáp án cần chọn là: A

Câu 10:

Trong hệ tọa độ Oxy, cho hai điểm $A (1; 2), B (- 2; 3)$ . Tìm tọa độ điểm I sao cho $\vec{I A} + 2 \vec{I B} = \vec{0}$

A. $I (1; 2)$

B. $I (1; \frac{2}{5})$

C. $I (- 1; \frac{8}{3})$

D. $I (2; - 2)$

Xem đáp án

Gọi I (x; y). Ta có: $\vec{I A} = (1 - x; 2 - y) \vec{I B} = (- 2 - x; 3 - y) \Rightarrow 2 \vec{I B} = (- 4 - 2 x; 6 - 2 y) \Rightarrow \vec{I A} + 2 \vec{I B} = (- 3 - 3 x; 8 - 3 y)$

Do đó từ giả thiết $\vec{I A} + 2 \vec{I B} = \vec{0} \Rightarrow \{\begin{matrix} - 3 - 3 x = 0 \\ 8 - 3 y = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x = - 1 \\ y = \frac{8}{3} \end{matrix}$

Đáp án cần chọn là: C

Câu 11:

Trong hệ tọa độ Oxy, cho tam giác ABC có C (−2; −4), trọng tâm G (0; 4) và trung điểm cạnh BC là M (2; 0). Tổng hoành độ của điểm A và B là

A. -2

B. 2

C. 4

D. 8

Xem đáp án

Vì M là trung điểm của BC nên $\{\begin{matrix} x_{B} = 2 x_{M} - x_{C} = 2.2 - (- 2) = 6 \\ y_{B} = 2 y_{M} - y_{C} = 2.0 - (- 4) = 4 \end{matrix} \Rightarrow B (6; 4)$

Vì G là trọng tâm tam giác ABC nên $\{\begin{matrix} x_{A} = 3 x_{G} - x_{B} - x_{C} = - 4 \\ y_{A} = 3 y_{G} - y_{B} - y_{C} = 12 \end{matrix} \Rightarrow A (- 4; 12)$

Suy ra x_A + x_B = 2

Đáp án cần chọn là: B

Câu 12:

Trong hệ tọa độ Oxy, cho tam giác ABC có A (1; −1), B(5; −3) và C thuộc trục Ox, trọng tâm G của tam giác thuộc trục Oy. Tìm tọa độ điểm C.

A. C (−6; 0).

B. C (−6; −1).

C. C (0; −1).

D. C (−1; 0).

Xem đáp án

Ta có: C thuộc trục Ox ⇒ C (x; 0), G nằm trên trục Oy ⇒ G (0; y)

G là trọng tâm tam giác ABC nên ta có: $\{\begin{matrix} 0 = \frac{1 + 5 + x}{3} \\ y = \frac{(- 1) + (- 3) + 0}{3} \end{matrix} \Leftrightarrow \{\begin{matrix} x = - 6 \\ y = - \frac{4}{3} \end{matrix}$

Vậy C (−6; 0)

Đáp án cần chọn là: A

Câu 13:

Trong hệ tọa độ Oxy, cho điểm M (3; -4). Gọi M₁, M₂ lần lượt là hình chiếu vuông góc của M trên Ox, Oy. Khẳng định nào đúng?

A. $\bar{O M_{1}} = - 3$

B. $\bar{O M_{2}} = 4$

C. $\vec{O M_{1}} - \vec{O M_{2}} = (- 3; - 4)$

D. $\vec{O M_{1}} + \vec{O M_{2}} = (3; - 4)$

Xem đáp án

Từ giả thiết, suy ra $M_{1} (3; 0), M_{2} (0; - 4)$ .

A sai vì $\bar{O M_{1}} = 3$ .

B sai vì $\bar{O M_{2}} = - 4$ .

C sai vì $\vec{O M_{1}} - \vec{O M_{2}} = \vec{M_{2} M_{1}} = (3; 4)$

Đáp án cần chọn là: D

Câu 14:

Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD có A (2; 3) và tâm I (−1; 1). Biết điểm M (4; 9) nằm trên đường thẳng AD và điểm D có tung độ gấp đôi hoành độ. Tìm các đỉnh còn lại của hình bình hành?

A. Tọa độ các đỉnh C (−4; −1), B (−5; −4), D (3; 6).

B. Tọa độ các đỉnh C (−4; −1), B (−4; −2), D (2; 4).

C. Tọa độ các đỉnh C (−4; −1), B (−1; 4), D (−1; −2).

D. Tọa độ các đỉnh C (4; 1), B (−5; −4), D (3; 6).

Xem đáp án

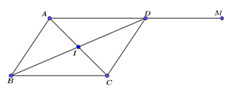
Ta có I là trung điểm của AC ⇒ C (−4; −1).

Điểm D có tung độ gấp đôi hoành độ ⇒ D (x_D; 2x_D).

Lại có $\vec{A M}$ = (2; 6), $\vec{A D}$ = (x_D− 2; 2x_D− 3).

Mà A, M, D thẳng hàng ⇒ 6(x_D− 2) = 2(2x_D− 3) ⇔ x_D= 3 ⇒ D (3; 6)

I là trung điểm BD ⇒ B (−5; −4)

Đáp án cần chọn là: A

Câu 15:

Cho M (−1; −2), N (3; 2), P (4; −1). Tìm E trên Ox sao cho $|\vec{E M} + \vec{E N} + \vec{E P}|$ nhỏ nhất.

A. E (4; 0).

B. E (3; 0).

C. E (1; 0).

D. E (2; 0).

Xem đáp án

Do $E \in Ox \Rightarrow E (a; 0)$

Ta có: $\vec{E M} = (- 1 - a; - 2); \vec{E N} = (3 - a; 2); \vec{E P} = (4 - a; - 1)$

Suy ra $|\vec{E M} + \vec{E N} + \vec{E P}| = \sqrt{{(6 - 3 a)}^{2} + {(- 1)}^{2}} = \sqrt{{(6 - 3 a)}^{2} + 1} \geq 1$

Giá trị nhỏ nhất của $|\vec{E M} + \vec{E N} + \vec{E P}|$ bằng 1

Dấu bằng xảy ra khi và chỉ khi 6 – 3a = 0 a = 2

Vậy E (2; 0).

Đáp án cần chọn là: D

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Hệ trục tọa độ có đáp án

Trắc nghiệm Hệ trục tọa độ có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương