10 câu hỏi trắc nghiệm thuộc Trắc nghiệm Tích của một vec tơ với một số có đáp án (Vận dụng)

Câu 1:

Cho ba điểm A, B, C không thẳng hàng và điểm M thỏa mãn đẳng thức vectơ $\vec{A M} = x \vec{A B} + y \vec{A C}$ . Đặt $\vec{M A} = x \vec{M B} + y \vec{M C}$ . Tính giá trị biểu thức P = x + y

A. P = 0

B. P = 2

C. P = -2

D. P = 3

Xem đáp án

Ta có:

$\vec{A M} = x \vec{A B} + y \vec{A C} \Leftrightarrow \vec{A M} = x (\vec{A M} + \vec{M B}) + y (\vec{A M} + \vec{M C})$

$\Leftrightarrow (1 - x - y) \vec{A M} = x \vec{M B} + y \vec{M C}$

$\Leftrightarrow (x + y - 1) \vec{M A} = x \vec{M B} + y \vec{M C}$

Theo bài ra, ta có: $\vec{M A} = x \vec{M B} + y \vec{M C}$

Suy ra $x + y - 1 = 1 \Leftrightarrow x + y = 2$

Đáp án cần chọn là: B

Câu 2:

Gọi AN, CM là các trung tuyến của tam giác ABC. Đẳng thức nào sau đây đúng ?

A. $\vec{A B} = \frac{2}{3} \vec{A N} + \frac{2}{3} \vec{C M}$

B. $\vec{A B} = \frac{4}{3} \vec{A N} - \frac{2}{3} \vec{C M}$

C. $\vec{A B} = \frac{4}{3} \vec{A N} + \frac{4}{3} \vec{C M}$

D. $\vec{A B} = \frac{4}{3} \vec{A N} + \frac{2}{3} \vec{C M}$

Xem đáp án

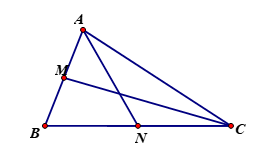
Ta có: $\vec{A N} = \frac{1}{2} (\vec{A B} + \vec{A C}) = \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C}$

$\vec{C M} = \vec{C A} + \vec{A M} \Rightarrow \frac{1}{2} \vec{C M} = \frac{1}{2} \vec{C A} + \frac{1}{2} \vec{A M}$

Suy ra

$\vec{A N} + \frac{1}{2} \vec{C M} = \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C} + \frac{1}{2} \vec{C A} + \frac{1}{2} \vec{A M}$

$= \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{A C} - \frac{1}{2} \vec{A C} + \frac{1}{2} . \frac{1}{2} \vec{A B} = \frac{3}{4} \vec{A B}$

Do đó $\vec{A B} = \frac{4}{3} \vec{A N} + \frac{2}{3} \vec{C M}$

Đáp án cần chọn là: D

Câu 3:

Cho hai điểm cố định A, B; gọi I là trung điểm AB. Tập hợp các điểm M thỏa: $|\vec{M A} + \vec{M B}| = |\vec{M A} - \vec{M B}|$ là:

A. Đường tròn đường kính AB

B. Trung trực của AB

C. Đường tròn tâm I, bán kính AB

D. Nửa đường tròn đường kính AB

Xem đáp án

Ta có: $|\vec{M A} + \vec{M B}| = |\vec{M A} - \vec{M B}|$

$\Leftrightarrow |2 \vec{M I}| = |\vec{B A}| \Leftrightarrow 2 M I = B A \Leftrightarrow M I = \frac{B A}{2}$

Vậy tập hợp các điểm M là đường tròn đường kính AB

Đáp án cần chọn là: A

Câu 4:

Tam giác ABC vuông tại A, AB = AC = 2. Độ dài vec tơ $4 \vec{A B} - \vec{A C}$ bằng:

A. $\sqrt{17}$

B. $2 \sqrt{15}$

C. 5

D. 2 $\sqrt{17}$

Xem đáp án

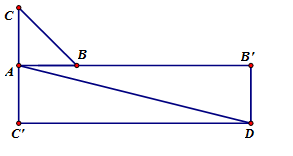
Vẽ $\vec{A B'} = 4 \vec{A B}; \vec{A C'} = - \vec{A C}$ . Vẽ hình bình hành AC’DB’

Ta có: $|4 \vec{A B} - \vec{A C}| = |\vec{A B'} + \vec{A C'}| = |\vec{A D}| = A D$

Do đó $A D = \sqrt{A B'^{2} + A C'^{2}} = \sqrt{8^{2} + 2^{2}} = 2 \sqrt{17}$

Đáp án cần chọn là: D

Câu 5:

Cho tam giác OAB vuông cân tại O, cạnh OA = a. Khẳng định nào sau đây sai?

A. $|3 \vec{O A} + 4 \vec{O B}| = 5 a$

B. $|2 \vec{O A}| + |3 \vec{O B}| = 5 a$

C. $|7 \vec{O A} - 2 \vec{O B}| = 5 a$

D. $|11 \vec{O A}| - |6 \vec{O B}| = 5 a$

Xem đáp án

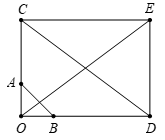
Dựa vào các đáp án, ta có nhận xét sau:

A đúng, gọi C nằm trên tia đối của tia AO sao cho $O C = 3 O A \Rightarrow 3 \vec{O A} = \vec{O C}$

Và D nằm trên tia đối của tia BO sao cho $O D = 4 O B \Rightarrow 4 \vec{O B} = \vec{O D}$

Dựng hình chữ nhật OCED suy ra (quy tắc hình bình hành)

Ta có

$|3 \vec{O A} + 4 \vec{O B}| = |\vec{O C} + \vec{O D}| = |\vec{O E}| = O E = C D = \sqrt{O C^{2} + O D^{2}} = 5 a$

B đúng, vì $|2 \vec{O A}| + |3 \vec{O B}| = 2 |\vec{O A}| + 3 |\vec{O B}| = 2 a + 3 a = 5 a$

C sai, xử lí tương tự như đáp án A

D đúng, vì $|11 \vec{O A}| - |6 \vec{O B}| = 11 |\vec{O A}| - 6 |\vec{O B}| = 11 a - 6 a = 5 a$

Đáp án cần chọn là: C

Câu 6:

Cho tam giác đều ABC cạnh a. Biết rằng tập hợp các điểm M thỏa mãn đẳng thức $|2 \vec{M A} + 3 \vec{M B} + 4 \vec{M C}| = |\vec{M B} - \vec{M A}|$ là đường tròn cố định có bán kính R. Tính bán kính R theo a

A. $R = \frac{a}{3}$

B. $R = \frac{a}{9}$

C. $R = \frac{a}{2}$

D. $R = \frac{a}{6}$

Xem đáp án

Gọi G là trọng tâm của tam giác ABC

Ta có: $2 \vec{M A} + 3 \vec{M B} + 4 \vec{M C}$

$= 2 (\vec{M I} + \vec{I A}) + 3 (\vec{M I} + \vec{I B}) + 4 (\vec{M I} + \vec{I C})$

Chọn điểm I sao cho $2 \vec{I A} + 3 \vec{I B} + 4 \vec{I C} = \vec{0}$

$\Leftrightarrow 3 (\vec{I A} + \vec{I B} + \vec{I C}) + \vec{I C} - \vec{I A} = \vec{0}$

Mà G là trọng tâm của tam giác ABC $\Rightarrow \vec{I A} + \vec{I B} + \vec{I C} = 3 \vec{I G}$

Khi đó $9 \vec{I G} + \vec{I C} - \vec{I A} = \vec{0} \Leftrightarrow 9 \vec{I G} + \vec{A I} + \vec{I C} = \vec{0}$

$\Leftrightarrow 9 \vec{I G} = \vec{C A}$ (*)

Do đó, $|2 \vec{M A} + 3 \vec{M B} + 4 \vec{M C}| = |\vec{M B} - \vec{M A}|$

$\Leftrightarrow |9 \vec{M I} + 2 \vec{I A} + 3 \vec{I B} + 4 \vec{I C}| = |\vec{A B}| \Leftrightarrow 9 M I = A B$

Vì I là điểm cố định thỏa mãn (*) nên tập hợp các điểm M cần tìm là đường tròn tâm I, bán kính $R = \frac{A B}{9} = \frac{a}{9}$

Đáp án cần chọn là: B

Câu 7:

Cho hai điểm A, B phân biệt và cố định, với I là trung điểm của AB. Tập hợp các điểm M thỏa mãn đẳng thức $|2 \vec{M A} + \vec{M B}| = |\vec{M A} + 2 \vec{M B}|$ là

A. đường trung trực của đoạn thẳng AB

B. đường tròn đường kính AB

C. đường trung trực đoạn thẳng IA

D. đường tròn tâm A, bán kính AB

Xem đáp án

Chọn điểm E thuộc đoạn AB sao cho $E B = 2 E A \Rightarrow 2 \vec{E A} + \vec{E B} = \vec{0}$

Chọn điểm F thuộc đoạn AB sao cho $F A = 2 F B \Rightarrow 2 \vec{F B} + \vec{F A} = \vec{0}$

Ta có:

$|2 \vec{M A} + \vec{M B}| = |\vec{M A} + 2 \vec{M B}| \Leftrightarrow |2 \vec{M E} + 2 \vec{E A} + \vec{M E} + \vec{E B}| = |2 \vec{M F} + 2 \vec{F B} + \vec{M F} + \vec{F A}|$

$\Leftrightarrow |3 \vec{M E} + \underset{\vec{0}}{\underset{⏟}{2 \vec{E A} + \vec{E B}}}| = |3 \vec{M F} + \underset{\vec{0}}{\underset{⏟}{2 \vec{F B} + \vec{F A}}}|$

$\Leftrightarrow |3 \vec{M E}| = |3 \vec{M F}| \Leftrightarrow M E = M F$ (*)

Vì E, F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF

Với I là trung điểm của AB suy ra I cũng là trung điểm của EF

Vậy tập hợp các điểm M thỏa mãn $|2 \vec{M A} + \vec{M B}| = |\vec{M A} + 2 \vec{M B}|$ là đường trung trực của đoạn thẳng AB

Đáp án cần chọn là: A

Câu 8:

Cho tam giác ABC, tập hợp các điểm M sao cho $|\vec{M A} + \vec{M B} + \vec{M C}| = 6$ là:

A. một đường thẳng đi qua trọng tâm của tam giác ABC

B. đường tròn có tâm là trọng tâm của tam giác ABC và bán kính bằng 6.

C. đường tròn có tâm là trọng tâm của tam giác ABC và bán kính bằng 2.

D. đường tròn có tâm là trọng tâm của tam giác ABC và bán kính bằng 18

Xem đáp án

Gọi G là trọng tâm của tam giác ABC, ta có $|\vec{M A} + \vec{M B} + \vec{M C}| = |3 \vec{M G}|$

Thay vào ta được: $|\vec{M A} + \vec{M B} + \vec{M C}| = 6$ $\Leftrightarrow |3 \vec{M G}| = 6 \Leftrightarrow M G = 2$ , hay tập hợp các điểm M là đường tròn có tâm là trọng tâm của tam giác ABC và bán kính bằng 2 .

Đáp án cần chọn là: C

Câu 9:

Cho tam giác ABC. Có bao nhiêu điểm M thỏa mãn $|\vec{M A} + \vec{M B} + \vec{M C}| = 3$

A. 1

B. 2

C. 3

D. Vô số

Xem đáp án

Gọi G là trọng tâm của tam giác ABC nên G cố định duy nhất và

$\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ . Ta có:

$|\vec{M A} + \vec{M B} + \vec{M C}| = 3$ $\Leftrightarrow |\vec{G A} + \vec{G B} + \vec{G C} - 3 \vec{G M}| = 3$

$\Leftrightarrow 3 |\vec{G M}| = 3 \Leftrightarrow G M = 1$

Vậy tập hợp các điểm M là đường tròn tâm G bán kính bằng 1

Đáp án cần chọn là: D

Câu 10:

Cho tứ giác ABCD. Trên cạnh AB, CD lấy lần lượt các điểm M, N sao cho $3 \vec{A M} = 2 \vec{A B}$ và $3 \vec{D N} = 2 \vec{D C}$ . Tính vectơ $\vec{M N}$ theo hai vec tơ $\vec{A D}, \vec{B C}$

A. $\vec{M N} = \frac{1}{3} \vec{A D} + \frac{1}{3} \vec{B C}$

B. $\vec{M N} = \frac{1}{3} \vec{A D} - \frac{2}{3} \vec{B C}$

C. $\vec{M N} = \frac{1}{3} \vec{A D} + \frac{2}{3} \vec{B C}$

D. $\vec{M N} = \frac{2}{3} \vec{A D} + \frac{1}{3} \vec{B C}$

Xem đáp án

Ta có: $\vec{M N} = \vec{M A} + \vec{A D} + \vec{D N}$ và $\vec{M N} = \vec{M B} + \vec{B C} + \vec{C N}$

Suy ra $3 \vec{M N} = \vec{M A} + \vec{A D} + \vec{D N} + 2 (\vec{M B} + \vec{B C} + \vec{C N})$

$= (\vec{M A} + 2 \vec{M B}) + \vec{A D} + 2 \vec{B C} + (\vec{D N} + 2 \vec{C N})$

Theo bài ra, ta suy ra:

$(\vec{M A} + 2 \vec{M B}) = \vec{0}$ và $(\vec{D N} + 2 \vec{C N}) = \vec{0}$

Vậy $3 \vec{M N} = \vec{A D} + 2 \vec{B C} \Leftrightarrow \vec{M N} = \frac{1}{3} \vec{A D} + \frac{2}{3} \vec{B C}$

Đáp án cần chọn là: C

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Tích của một vec tơ với một số có đáp án

Trắc nghiệm Tích của một vec tơ với một số có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương