Trắc nghiệm Tích của một vec tơ với một số có đáp án (Thông hiểu)
-
2592 lượt thi
-
13 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
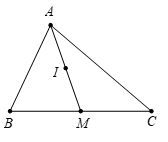
Vì M là trung điểm BC nên (1)
Mặt khác I là trung điểm AM nên (2)
Từ (1), (2) suy ra
Đáp án cần chọn là: A
Câu 2:
Nếu G là trọng tâm tam giác ABC thì đẳng thức nào sau đây đúng?
 Xem đáp án
Xem đáp án
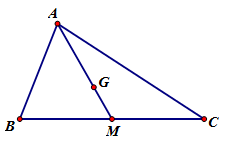
Gọi M là trung điểm của BC nên ta có
Mà
Đáp án cần chọn là: B
Câu 3:
Cho tam giác ABC có M là trung điểm của BC, G là trọng tâm của tam giác. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
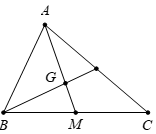
Vì G là trọng tâm tam giác ABC
Vì M là trung điểm của BC
Do đó
Đáp án cần chọn là: B
Câu 4:
Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM. Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
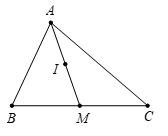
Vì M là trung điểm BC nên
Mặt khác I là trung điểm AM nên
Suy ra
Đáp án cần chọn là: B
Câu 5:
Phát biểu nào là sai?
 Xem đáp án
Xem đáp án
thì
Nên đáp án A đúng và B sai vì A, B, C, D không nhất thiết phải thẳng hàng.
Đáp án cần chọn là: B
Câu 6:
Cho tam giác ABC và đặt . Cặp vec tơ nào sau đây cùng phương ?
 Xem đáp án
Xem đáp án
Dễ thấy
Hai vec tơ cùng phương
Đáp án cần chọn là: C
Câu 8:
Cho tam giác OAB vuông cân tại O, cạnh OA = a. Tính
 Xem đáp án
Xem đáp án
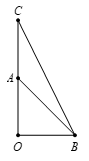
Gọi C là điểm đối xứng của O qua A ⇒ OC = 2a.
Tam giác OBC vuông tại O, có
Ta có:
Suy ra
Đáp án cần chọn là: C
Câu 9:
Biết rằng hai vec tơ và không cùng phương nhưng hai vec tơ và cùng phương. Khi đó giá trị của x là:
 Xem đáp án
Xem đáp án
Ta có và cùng phương nên có tỉ lệ:
Đáp án cần chọn là: C
Câu 10:
Cho tam giác ABC và điểm M thỏa mãn . Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Gọi I, G lần lượt là trung điểm BC và trọng tâm tam giác ABC.
Vì I là trung điểm BC nên
Theo bài ra, ta có suy ra ⇒ A, M, I thẳng hàng
Mặt khác G là trọng tâm của tam giác ABC ⇒ G ∈ AI.
Do đó, ba điểm A, M, G thẳng hàng.
Đáp án cần chọn là: C
Câu 11:
Cho tam giác ABC, điểm M thỏa mãn: . Với mỗi điểm I bất kì, nếu thì cặp số bằng:
 Xem đáp án
Xem đáp án
Ta có:
Đáp án cần chọn là: A
Câu 12:
Cho tam giác ABC. Gọi M là điểm trên cạnh BC sao cho MB = 3MC. Khi đó, biểu diễn theo và là:
 Xem đáp án
Xem đáp án
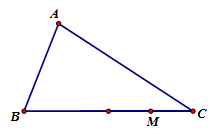
Ta có:
Đáp án cần chọn là: B