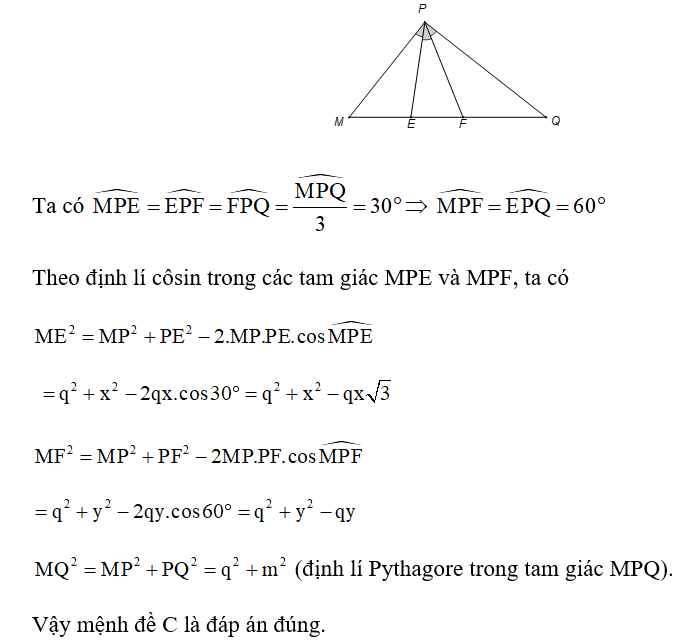
Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2) (Thông hiểu)
-
1033 lượt thi
-
8 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 3 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích tam giác mới được tạo nên bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Có S = BC.CA.sinC
Gọi S’ là diện tích tam giác khi tăng cạnh BC lên 3 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn góc C
Ta có: S’ = .3BC.3CA.sinC = 9 . BC.CA.sinC = 9S.
Câu 2:
Cho tam giác ABC có AB = 10 cm, AC = 20 cm và có diện tích là 90 cm2. Giá trị sinA là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: S = AB.AC.sinA sinA = = = .
Câu 3:
Tam giác ABC có AB = 4, BC = 6, AC = . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
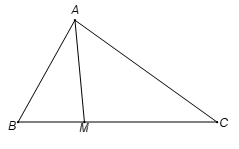
Câu 4:
Tam giác ABC có AB = , BC = , CA = . Gọi D là chân đường phân giác trong góc A. Khi đó góc bằng bao nhiêu độ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C

Câu 5:
Để đo khoảng cách từ một điểm A bên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C. Ta đo được khoảng cách AB = 40 m, = 45° và = 70°. Vậy sau khi đo đạc và tính toán được, khoảng cách AC gần nhất với giá trị nào sau đây?
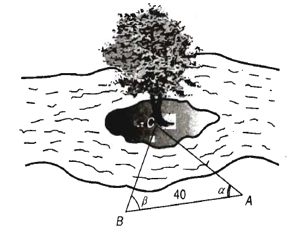
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ định lí tổng ba góc trong tam giác ABC, suy ra .
Do đó, .
Áp dụng định lí sin vào tam giác ABC, ta có .
Suy ra AC = ≈ 41,47 (m) ≈ 41,5 (m).
Câu 6:
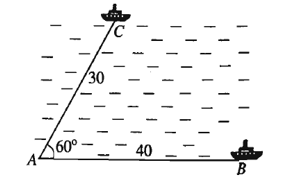
Hai chiếc tàu thuỷ cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc 60°. Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ. Sau hai giờ hai tàu cách nhau bao nhiêu hải lí? (kết quả gần nhất).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Sau hai giờ tàu B đi được 20 . 2 = 40 hải lí, tàu C đi được 15 . 2 = 30 hải lí. Vậy tam giác ABC có AB = 40, AC = 30 và = 60°.
Áp dụng định lí côsin vào tam giác ABC, ta có
BC2 = AC2 + AB2 – 2AC.AB.cosA = 302 + 402 – 2.30.40.cos60° = 900 + 1600 – 1200 = 1300
Vậy BC = ≈ 36 (hải lí).
Sau 2 giờ, hai tàu đang cách nhau khoảng 36 hải lí.