5 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2) (Vận dụng)

Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2)

Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2) (Vận dụng)

746 lượt thi
5 câu hỏi
60 phút

Danh sách câu hỏi

Câu 1:

Cho $\hat{x O y}$ = 30°. Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài đoạn OA bằng:

\frac{3}{2}

;

\sqrt{3}

;

2 \sqrt{2}

;

D. 2.

Xem đáp án

Đáp án đúng là: B

Theo định lí sin trong tam giác OAB, ta có:

$\frac{O B}{\sin \hat{O A B}} = \frac{A B}{\sin \hat{A O B}}$

$\Leftrightarrow O B = \frac{A B}{\sin \hat{A O B}} . \sin \hat{O A B}$

$\Rightarrow O B = \frac{1}{\sin 30 °} . \sin \hat{O A B} = 2 \sin \hat{O A B}$

Do đó, độ dài OB lớn nhất khi và chỉ khi

sin $\hat{O A B}$ = 1 $\Rightarrow$ $\hat{O A B}$ = 90°

Khi đó OB = 2.

Tam giác OAB vuông tại A Þ OA = $\sqrt{O B^{2} - A B^{2}}$ = $\sqrt{2^{2} - 1}$ = $\sqrt{3}$ .

Câu 2:

Tam giác ABC vuông tại A, có AB = c, AC = b. Gọi D là chân đường phân giác trong góc A. Tính AD theo b và c.

A. AD = $\frac{\sqrt{2} b c}{b + c}$ ;

B. AD =

\frac{2 (b + c)}{b c}

;

C. AD =

\frac{2 b c}{b + c}

;

D. AD =

\frac{\sqrt{2} (b + c)}{b c}

Xem đáp án

Đáp án đúng là: A

Tam giác ABC vuông tại A, có AB = c, AC = b. Gọi D là chân đường phân giác trong góc A. Tính AD theo b và c. (ảnh 1)

Câu 3:

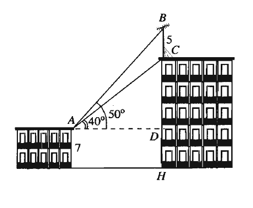
Trên nóc một toà nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50° và 40° so với phương nằm ngang. Chiều cao của toà nhà gần nhất với giá trị nào sau đây?

Trên nóc một toà nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của (ảnh 1)

A. 12 m;

B. 19 m;

C. 24 m;

D. 29 m.

Xem đáp án

Đáp án đúng là: B

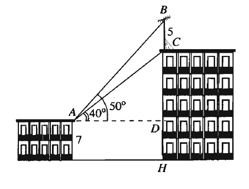
Trên nóc một toà nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của (ảnh 2)

Từ hình vẽ, suy ra $\hat{B A C}$ = 50° – 40° = 10° và $\hat{A B D} = 180 ° - (\hat{B A D} + \hat{A D B}) = 180 ° - (50 ° + 90 °) = 40 °$

Áp dụng định lí sin trong tam giác ABC, ta có $\frac{B C}{\sin \hat{B A C}} = \frac{A C}{\sin \hat{A B C}} \Rightarrow A C = \frac{B C . \sin \hat{A B C}}{\sin \hat{B A C}} = \frac{5. \sin 40 °}{\sin 10 °} \approx 18,5 m$

Trong tam giác vuông ADC, ta có $\sin \hat{C A D} = \frac{C D}{A C} \Rightarrow C D = A C . \sin \hat{C A D} = 11,9 m.$

Suy ra CH = CD + DH = 11,9 + 7 = 18,9 m ≈ 19 m.

Vậy chiều cao tòa nhà khoảng 19 m.

Câu 4:

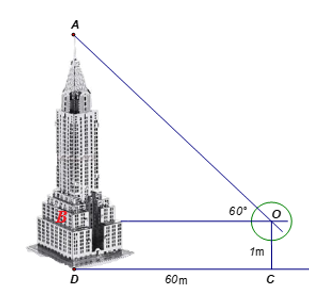
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng CD = 60 m, giả sử chiều cao của giác kế là OC = 1 m. Quay thanh giác kế sao cho khi ngắm theo thanh ta nhìn thấy đỉnh A của tháp. Đọc trên giác kế số đo của góc $\hat{A O B}$ = 60°. Chiều cao của ngọn tháp gần với giá trị nào sau đây:

Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng (ảnh 1)

A. 40 m;

B. 114 m;

C. 105 m;

D. 110 m.

Xem đáp án

Đáp án đúng là: C

Tam giác OAB vuông tại B, có $\tan \hat{A O B} = \frac{A B}{O B}$ $\Rightarrow A B = \tan 60 ° . O B = 60 \sqrt{3} m .$

Vậy chiều cao của ngọn tháp là: $h = A B + O C = (60 \sqrt{3} + 1) m \approx 105 m .$

Câu 5:

Từ hai vị trí A và B của một toà nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30’. Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?

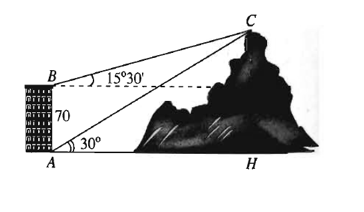
Từ hai vị trí A và B của một toà nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m (ảnh 1)

A. 135 m;

B. 234 m;

C. 165 m;

D. 195 m.

Xem đáp án

Đáp án đúng là: A

Từ giả thiết, ta suy ra tam giác ABC có $\hat{C A B} = 90 ° - 30 ° = 60 °$ , $\hat{A B C} = 90 ° + 15 ° 30^{'} = 105 ° 30^{'}$ và AB = 70.

Theo định lí tổng ba góc trong tam giác ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$

$\Rightarrow \hat{C} = 180 ° - (\hat{A} + \hat{B}) = 180 ° - (60 ° + 105 ° 30^{'}) = 14 ° 30^{'} .$

Theo định lí sin trong tam giác ABC, ta có $\frac{A C}{\sin B} = \frac{A B}{\sin C}$ hay $\frac{A C}{\sin 105 ° 30^{'}} = \frac{70}{\sin 14 ° 30^{'}}$ .

Do đó $A C = \frac{70. \sin 105 ° 30^{'}}{\sin 14 ° 30^{'}} \approx 269,4 m .$

Gọi CH là khoảng cách từ C đến mặt đất. Tam giác vuông ACH có cạnh CH đối diện với góc 30° nên $C H = \frac{A C}{2} = \frac{269,4}{2} = 134,7 m \approx 135 m.$

Vậy ngọn núi cao khoảng 135 m.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2)

Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2) (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương