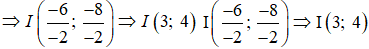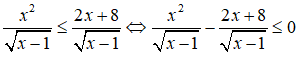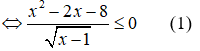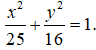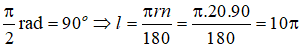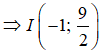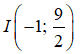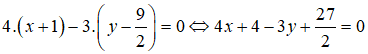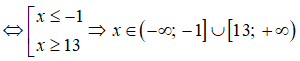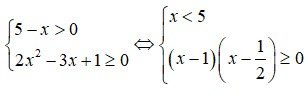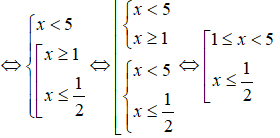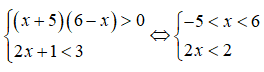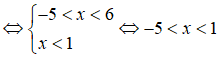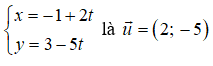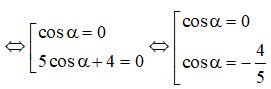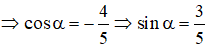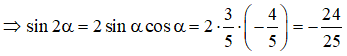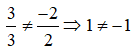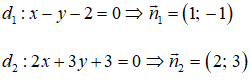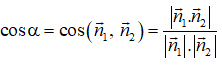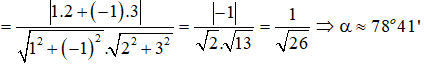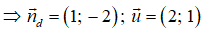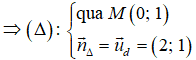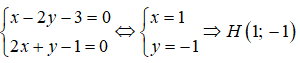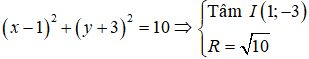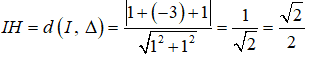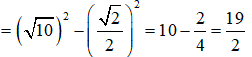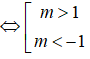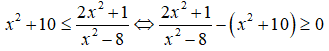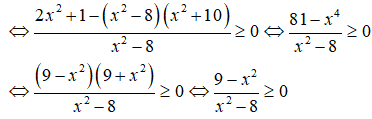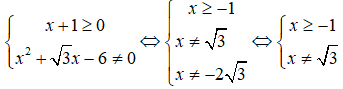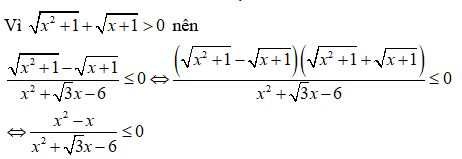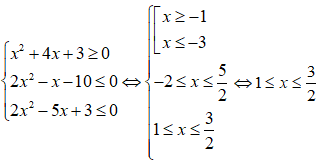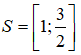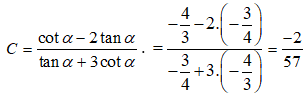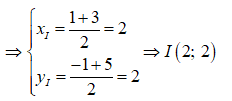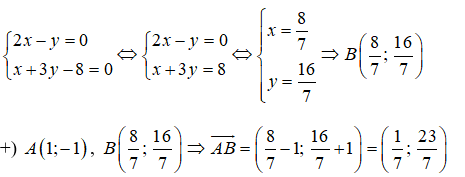Đề thi Học kì 2 Toán 10 có đáp án (Đề 3)
-
2042 lượt thi
-
23 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Phần I: Trắc nghiệm
Cho . Kết quả đúng là:
 Xem đáp án
Xem đáp án
Chọn C.
Ta có:
⇒ Điểm cuối của góc α thuộc góc phần tư thứ hai của đường tròn lượng giác .
⇒ sinα > 0, cos α < 0
Câu 3:
Số nghiệm nguyên của bất phương trình là
 Xem đáp án
Xem đáp án
Chọn A.
Điều kiện: x > 1
Vì 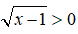
Kết hợp với điều kiện x > 1 suy ra 1 ≤ x ≤ 4 ⇒ x ∈ {2;3;4}
Vậy bất phương trình có ba nghiệm nguyên.
Câu 4:
Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6. Phương trình nào sau đây là phương trình của elip (E).
 Xem đáp án
Xem đáp án
Chọn A.
Độ dài trục lớn bằng 10 ⇒ 2a = 10 ⇔ a = 5, = 25
Độ dài tiêu cự bằng 6 ⇒ 2c = 6 ⇔ c = 3
Ta có: - = ⇒ = - = - = 16
Vậy phương trình của elip (E) là:
Câu 5:
Độ dài của cung có số đo π/2 rad, trên đường tròn bán kính r=20 là:
 Xem đáp án
Xem đáp án
Chọn D.
Ta có:
Vậy l = 10π.
Câu 7:
Cho hai điểm A(-3;6) và B(1;3). Phương trình đường trung trực của AB là:
 Xem đáp án
Xem đáp án
Chọn C.
+ Gọi I là trung điểm của AB
+ A(-3;6),B(1;3)
+ Phương trình đường trung trực của AB đi qua
và nhận 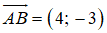
⇔ 8x + 8 - 6y + 27 = 0 ⇔ 8x - 6y + 35 = 0
Câu 8:
Trong các phương trình sau, phương trình nào là phương trình đường tròn?
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình đường tròn có hệ số của và bằng nhau ⇒ Loại đáp án A và C
Xét đáp án B: + - 4x - 8y + 1 = 0 ⇒ a = 2, b = 4, c = 1 ⇒ + - c > 0 ⇒ Nhận
Xét đáp án C: + - 2x - 8y + 30 = 0 ⇒ a = 1, b = 4, c = 30 ⇒ + - c < 0 ⇒ Loại
Câu 9:
Tam thức bậc hai f(x) = - 12x - 13 nhận giá trị không âm khi và chỉ khi:
 Xem đáp án
Xem đáp án
Chọn D.
Tam thức bậc hai f(x) = - 12x - 13 nhận giá trị không âm khi và chỉ khi
f(x) ≥ 0 ⇔ - 12x - 13 ≥ 0
Câu 10:
Điều kiện của bất phương trình là:
 Xem đáp án
Xem đáp án
Chọn C.
Điều kiện xác định của bất phương trình là:
Câu 13:
Cho góc α thỏa mãn và sinα + 2cosα = -1. Giá trị sin2α là:
 Xem đáp án
Xem đáp án
Chọn D.
Vì 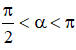
Từ sinα + 2cosα = -1 ⇒ sinα = -1 - 2cosα.
Ta có:
(-1 - 2cosα + = 1
⇔ 1 + 4cosα + 4 + = 1
⇔ 5cos2α + 4cosα = 0
⇔ cosα.(5cosα + 4) = 0
Câu 14:
Đường thẳng Δ: 3x-2y-7=0 cắt đường thẳng nào sau đây?
 Xem đáp án
Xem đáp án
Chọn A.
Xét đường thẳng Δ: 3x - 2y - 7 = 0 và d1: 3x + 2y = 0 ta có:
Câu 16:
Cho đường thẳng d: x - 2y - 3 = 0. Tọa độ hình chiếu vuông góc H của điểm M(0;1) trên đường d là:
 Xem đáp án
Xem đáp án
Chọn D.
Gọi Δ là đường thẳng đi qua M và vuông góc với đường thẳng d.
d: x - 2y - 3 = 0
⇒ 2.(x - 0) + 1.(y - 1) = 0 ⇔ 2x + y - 1 = 0
Gọi H = d ∩ (Δ). Tọa độ điểm H là nghiệm của hệ phương trình:
Câu 17:
Cho đường tròn (C): (x - 1 + (y + 3 = 10 và đường thẳng Δ: x + y + 1 = 0, biết đường tròn (C) cắt Δ tại hai điểm phân biệt A và B. Độ dài đoạn thẳng AB bằng:
 Xem đáp án
Xem đáp án
Chọn B.
Vì đường tròn (C) cắt Δ tại hai điểm phân biệt A và B nên tọa độ điểm A và B là nghiệm của hệ phương trình:
Gọi H là trung điểm của AB suy ra IH ⊥ AB ⇒ IH ⊥ Δ.
Xét tam giác AIH vuông tại H ta có:
A + I = A ⇒ A = A - I
Câu 18:
Giá trị của m để phương trình (m - 1) - (2m - 2)x + 2m = 0 vô nghiệm là:
 Xem đáp án
Xem đáp án
Chọn C.
Với m = 1 thỏa mãn yêu cầu bài toán
Với m ≠ 1 phương trình vô nghiệm khi và chỉ khi Δ' < 0
⇔ (m - 1 - 2m(m - 1) < 0 ⇔ (m - 1)(-m - 1) < 0
Vậy với 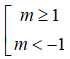
Câu 19:
Cho tam giác ABC có A(-2;0), B(0;3), C(3;1). Đường thẳng đi qua B và song song với AC có phương trình:
 Xem đáp án
Xem đáp án
Chọn D.
Gọi (d) là đường thẳng cần tìm. Do (d) song song với AC nên nhận 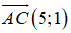
Suy ra 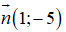
⇒ (d) có phương trình: 1(x - 0) - 5(y - 3) = 0 ⇔ x - 5y + 15 = 0
Câu 20:
Tập nghiệm của bất phương trình là:
 Xem đáp án
Xem đáp án
Chọn C.
Ta có
Bảng xét dấu
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là S = [-3;-2) ∪ (2;3].
Câu 21:
Phần II: Tự luận
Giải các bất phương trình và hệ bất phương trình:
a)
b)
 Xem đáp án
Xem đáp án
a) ĐKXĐ:
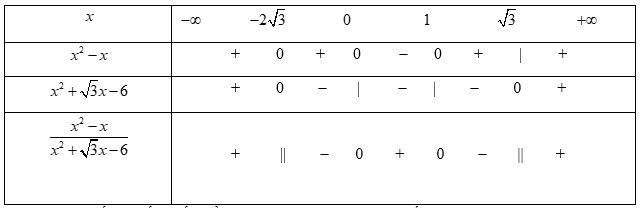
Bảng xét dấu
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là S = [-1;0]∪[1;√3)
b) Ta có:
Vậy tập nghiệm hệ bất phương trình là
Câu 23:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại B với A(1;-1), C(3;5). Điểm B nằm trên đường thẳng d: 2x - y = 0. Phương trình các đường thẳng AB, BC lần lượt là ax + by - 24 = 0, cx + dy + 8 = 0. Tính giá trị biểu thức a.b.c.d.
 Xem đáp án
Xem đáp án
Giả sử I(xI;yI) là trung điểm của AC
Vì tam giác ABC cân tại B nên BI ⊥ AC. Phương trình đường thẳng BI đi qua I(2;2) nhận 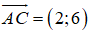
2.(x - 2) + 6.(y - 2) = 0 ⇔ 2x - 4 + 6y - 12 = 0 ⇔ 2x + 6y - 16 = 0 ⇔ x + 3y - 8 = 0
Tọa độ giao điểm B của BI và d là nghiệm của hệ phương trình:
Phương trình đường thẳng AB đi qua A(1;-1) nhận 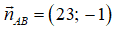
23.(x - 1) - 1.(y + 1) = 0 ⇔ 23x - 23 - y - 1 = 0 ⇔ 23x - y - 24 = 0
⇒ a = 23; b = -1
Phương trình đường thẳng BC đi qua C(3;5) nhận 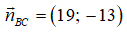
19.(x - 3) + (-13).(y - 5) = 0 ⇔ 19x - 57 - 13y + 65 = 0 ⇔ 19x - 13y + 8 = 0
⇒ c = 19; d = -13
⇒ a.b.c.d = 23.(-1).19.(-13) = 5681
Vậy a.b.c.d = 5681.