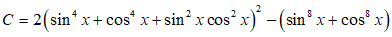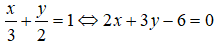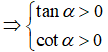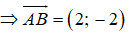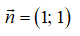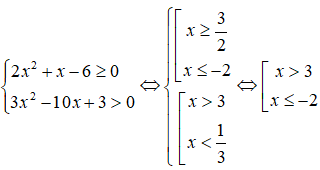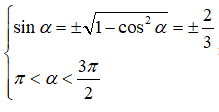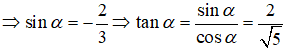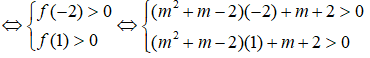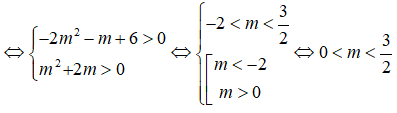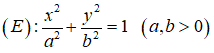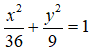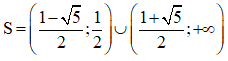14 câu hỏi trắc nghiệm thuộc Đề thi Học kì 2 Toán 10 có đáp án (Đề 4)

Câu 1:

Phần I: Trắc nghiệm

VTCP của đường thẳng $\frac{x}{3} + \frac{y}{2} = 1$ là:

A. $\vec{u} = (- 2; 3)$

B. $\vec{u} = (3; - 2)$

C. $\vec{u} = (3; 2)$

D. $\vec{u} = (2; 3)$

Xem đáp án

Chọn B.

Ta có:

⇒ Đường thẳng có VTPT là $\vec{n} = (2; 3)$ . Suy ra VTCP là $\vec{u} = (3; - 2)$

Câu 2:

Cho $2 π < α < \frac{5 π}{2}$ . Khẳng định nào sau đây đúng?

A. cot⁡α > 0

B. cot⁡α < 0.

C. cot⁡α < 0.

D. cot⁡α > 0.

Xem đáp án

Chọn A.

Ta có: $2 π < α < \frac{5 π}{2}$

⇒ Điểm cuối cùng α - π thuộc góc phần tư thứ I

Câu 3:

Vectơ pháp tuyến của đường thẳng đi qua hai điểm A(2;3) và B(4;1) là:

A. $\vec{n_{1}} = (2; - 2)$

B. $\vec{n_{2}} = (2; - 1)$

C. $\vec{n_{3}} = (1; 1)$

D. $\vec{n_{4}} = (1; - 2)$

Xem đáp án

Chọn C.

Ta có: A(2;3), B(4;1)

⇒ VTPT đi qua hai điểm A(2;3) và B(4;1) là

Câu 4:

Tập nghiệm của hệ bất phương trình $\{\begin{cases} 2 x^{2} + x - 6 > 0 \\ 3 x^{2} - 10 x + 3 > 0 \end{cases}$ là:

A. S = ( $- \infty$ ;-2]

B. S = (3; $+ \infty$ )

C. S = (-2;3)

D. S = ( $- \infty$ ;-2]∪(3; $+ \infty$ )

Xem đáp án

Chọn D.

Ta có

Vậy tập nghiệm hệ bất phương trình là S = ( $- \infty$ ;-2] ∪ (3; $+ \infty$ ).

Câu 5:

Cho góc α thỏa mãn $\cos α = - \frac{\sqrt{5}}{3} v à π < α < \frac{3 π}{2}$ . Tính tan⁡α.

A. $\tan α = - \frac{3}{\sqrt{5}}$

B. $\tan α = \frac{2}{\sqrt{5}}$

C. $\tan α = - \frac{4}{\sqrt{5}}$

D. $\tan α = - \frac{2}{\sqrt{5}}$

Xem đáp án

Chọn B.

Ta có :

Câu 6:

Giá trị của m để bất phương trình $m^{2}$ x + m(x + 1) - 2(x - 1) > 0 nghiệm đúng với mọi x ∈ [-2;1] là:

A. $0 < m < \frac{3}{2}$

B. $0 < m$

C. $m < \frac{3}{2}$

D. $[\begin{matrix} m < 0 \\ m > \frac{3}{2} \end{matrix}$

Xem đáp án

Chọn A.

Đặt: f(x) = ( $m^{2}$ + m – 2)x + m + 2

Bài toán thỏa mãn:

Câu 7:

Phương trình đường thẳng Δ đi qua điểm M(2;-5) và có hệ số góc k = -2 là:

A. y = -2x - 1

B. y = -2x - 9

C. y = 2x - 1

D. y = 2x - 9

Xem đáp án

Chọn B.

Phương trình đường thẳng Δđi qua điểm M(2;-5) và có hệ số góc k = -2 là:

y = -2(x - 2) - 5 ⇔ y = -2x - 1

Câu 8:

Trong mặt phẳng với hệ trục tọa độ Oxy, cho elip (E) có độ dài trục lớn bằng 12 và độ dài trục bé bằng 6. Phương trình nào sau đây là phương trình của elip (E).

A. $\frac{x^{2}}{144} + \frac{y^{2}}{36} = 1$

B. $\frac{x^{2}}{9} + \frac{y^{2}}{36} = 1$

C. $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$

D. $\frac{x^{2}}{144} + \frac{y^{2}}{36} = 0$

Xem đáp án

Chọn C.

Phương trình chính tắc của elip có dạng (E):

Ta có a = 6, b = 3, vậy phương trình của Elip là:

Câu 9:

Cho hai điểm A(1;2) và B(4;6). Tọa độ điểm M trên trục Oy sao cho diện tích tam giác MAB bằng 1 là:

A. $(0; \frac{13}{4}) v à (0; \frac{9}{4})$

B. (1;0)

C. (4;0)

D. (0;2)

Xem đáp án

Chọn A.

Hai điểm A(1;2) và B(4;6) ⇒ AB = 5

Gọi M(0;m).

Vì diện tích tam giác MAB bằng 1

Câu 10:

Trong mặt phẳng tọa độ Oxy, đường tròn (C) tâm I(-3;4), bán kính R = 6 có phương trình là:

A. (x + 3 $)^{2}$ + (y - 4 $)^{2}$ = 36

B. (x - 3 $)^{2}$ + (y + 4 $)^{2}$ = 6

C. (x + 3 $)^{2}$ + (y - 4 $)^{2}$ = 6

D. (x - 3 $)^{2}$ + (y + 4 $)^{2}$ = 36

Xem đáp án

Chọn A.

Phương trình đường tròn (C) tâm I(-3;4), bán kính R = 6 là:

[x - (-3) $]^{2}$ + (y - 4 $)^{2}$ = $6^{2}$ ⇒ (x + 3 $)^{2}$ + (y - 4 $)^{2}$ = 36

Câu 11:

Phần II: Tự luận

Giải các bất phương trình sau:

a) $(1 - 2 x) (x^{2} - x - 1) > 0$

b) $\frac{x^{2} - 1}{(x^{2} - 3) (- 3 x^{2} + 2 x + 8)} > 0$

Xem đáp án

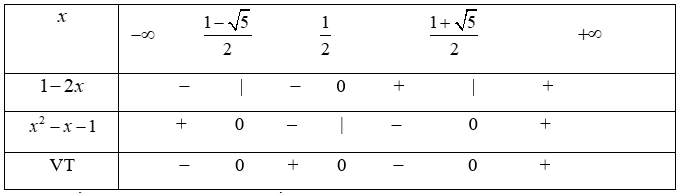
a) Bảng xét dấu

Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là:

b) Bảng xét dấu

Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là:

Câu 12:

Tìm tất cả các giá trị của tham số m để hệ bất phương trình sau có nghiệm.

$\{\begin{cases} x^{2} - 3 x + 2 \leq 0 \\ m x^{2} - 2 (2 m + 1) + 5 m + 3 \geq 0 \end{cases}$

Xem đáp án

Ta có bất phương trình $x^{2}$ - 3x + 2 ≤ 0 ⇔ 1 ≤ x ≤ 2.

Yêu cầu bài toán tương đương với bất phương trình:

m $x^{2}$ – 2(2m + 1)x + 5m + 3 ≤ 0 (1) có nghiệm x ∈ S = [1;2].

Ta đi giải bài toán phủ định là: Tìm m để bất phương trình (1) vô nghiệm trên S

Tức là bất phương trình f(x) = m $x^{2}$ - 2(2m + 1)x + 5m + 3 < 0 (2) đúng với mọi x ∈ S.

• m = 0 ta có (2) -2x + 3 < 0 ⇔ x > 3/2 nên (2) không đúng với ∀x ∈ S

• m ≠ 0 tam thức f(x) có hệ số a = m, biệt thức Δ' = - $m^{2}$ + m + 1

Bảng xét dấu

Câu 13:

Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào x.

A = 2( $\sin^{4} x$ + $\cos^{4} x$ + $\sin^{2} x$ . $\cos^{2} x$ $)^{2}$ - ( $\sin^{8} x$ + $\cos^{8} x$ )

Xem đáp án

Ta có:

Vậy giá trị của biểu thức không phụ thuộc vào x.

Câu 14:

Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;4), trọng tâm $G (2; \frac{2}{3})$ . Biết rằng đỉnh B nằm trên đường thẳng d: x + y + 2 = 0 và đỉnh C có hình chiếu vuông góc trên d là điểm H(2;-4). Giả sử B(a;b). Tính giá trị của biểu thức P = a - 3b.

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Học kì 2 Toán 10 có đáp án (Đề 1)

Đề thi Học kì 2 Toán 10 có đáp án (Đề 4)

Danh sách câu hỏi

Phần I: Trắc nghiệm

Phần II: Tự luận

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương