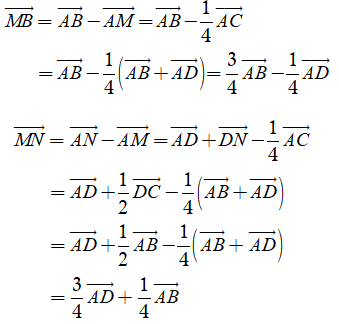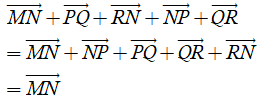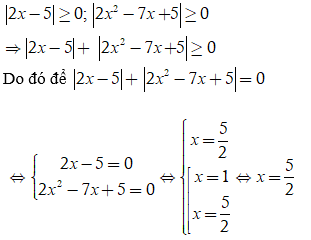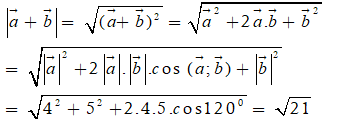41 câu hỏi trắc nghiệm thuộc Đề thi Toán lớp 10 Học kì 1 năm 2020 - 2021 có đáp án (Đề 3)

Câu 1:

Trong các phát biểu sau, phát biểu nào là mệnh đề đúng:

A. π là một số hữu tỉ

B. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba

C. Bạn có chăm học không?

D. Con thì thấp hơn cha

Xem đáp án

Đáp án B

Câu 2:

Cho tam giác ABC vuông tại C có AC = 9; BC = 5. Tính $\vec{AB} . \vec{AC}$

A. -27

B. 81

C. 9

D. -18

Xem đáp án

Câu 3:

Phủ định của mệnh đề “Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề nào sau đây:

A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn

B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn

C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn

D. Mọi số vô tỷ đều là số thập phân tuần hoàn

Xem đáp án

Đáp án C

Câu 4:

Trong các tập hợp sau, tập hợp nào là tập hợp rỗng:

A. $\{x \in Z / |x| < 1\}$

B. $\{x \in Z / 6 x^{2} - 7 x + 1 = 0\}$

C.

Xem đáp án

Đáp án C

Xét phương trình:

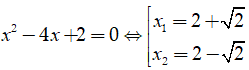
Không có số nào là số hữu tỉ nên tập C là tập rỗng

Câu 5:

Cho hai tập hợp A ={2,4,6,9} và B = {1,2,3,4}. Tập hợp A\ B bằng tập nào sau đây?

A. {1;2;3;5}

B. {1;3;6;9}

C. {6;9}

D. $\emptyset$

Xem đáp án

Đáp án C

Câu 6:

Tìm tập xác định D của hàm số $y = \frac{x^{2} + 1}{x^{2} + 3 x - 4}$

A. D = {1;-4}

B. D = R\{1;-4}

C. D = R\{1;4}

D. D = R

Xem đáp án

Đáp án B

Hàm số xác định khi

Vậy tập xác định của hàm số là D = R\ {1; -4}

Câu 7:

Cho A = [1; 4], B = (2; 6), C = (1; 2). Tìm A $\cap$ B $\cap$ C

A. [0;4]

B. [5; $+ \infty$ )

C. ( $- \infty$ ;1)

D. $\emptyset$

Xem đáp án

Đáp án D

Câu 8:

Cho A = {x $\in$ R: x+2 $\geq$ 0}, B = {x $\in$ R: 5-x $\geq$ 0}. Khi đó A $\cap$ B là:

A. [-2;5]

B. [-2;6]

C. [-5;2]

D. (-2; $+ \infty$ )

Xem đáp án

Đáp án A

Câu 9:

Tìm m để hàm số y = -( $m^{2}$ +1)x + m - 4 nghịch biến trên R.

A. m > 1

B. Với mọi m

C. m < -1

D. m > -1

Xem đáp án

Câu 10:

Cho tam giác ABC có AB= AC và đường cao AH. Đẳng thức nào sau đây đúng?

A. $\vec{AB} + \vec{AC} = \vec{AH}$

B. $\vec{HB} + \vec{HC} + \vec{HA} = \vec{0}$

C. $\vec{HB} + \vec{HC} = \vec{0}$

D. $\vec{AB} = \vec{AC}$

Xem đáp án

Đáp án C

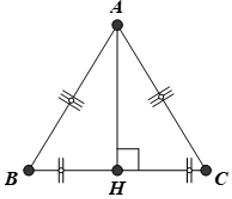
Do tam giác ABC có AB= AC nên tam giác ABC cân tại A.

Lại có, AH là đường cao nên đồng thời là đường trung tuyến hay H là trung điểm của BC.

Ta có $\vec{HB} + \vec{HC} = \vec{0}$ vì H là trung điểm của BC.

Phân tích:

Phương án A sai vì H là trung điểm của BC nên $\vec{AB} + \vec{AC} = 2 \vec{AH}$ :

Phương án B sai vì $\vec{HB} + \vec{HC} + \vec{HC} = \vec{HA}$ .

Phương án D sai vì các vectơ không cùng phương.

Câu 11:

Cho tam giác ABC với A(2;4), B(1;2). Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB

A. D(5;0)

B. D(7;0)

C. D(7,5;0)

D. Tất cả sai

Xem đáp án

Câu 12:

Tìm tất cả các giá trị thực của tham số m để hàm số y = $\frac{mx}{\sqrt{x - m + 2} - 1}$ xác định trên (0; 1)

A. $m \in (- \infty; 1)$

B. $m \in (- \infty; 1) \cup \{2\}$

C. $m \in (- \infty; 1) \cup (2; + \infty)$

D. $m \in (- \infty; 1] \cup \{2\}$

Xem đáp án

Câu 13:

Trong các hàm số y = 2015x; y = 2015 x + 2; y = 3 $x^{2}$ – 1; y = 2 $x^{3}$ – 3x có bao nhiêu hàm số lẻ?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án B

Câu 14:

Cho hình thoi ABCD tâm O, cạnh 2a. Góc $\hat{BAD} = 60^{0}$ . Tính độ dài vectơ $\vec{AB} + \vec{AD}$

A. $|\vec{AB} + \vec{AD}| = 2 a \sqrt{3}$

B. $|\vec{AB} + \vec{AD}| = a \sqrt{3}$

C. $|\vec{AB} + \vec{AD}| = 3 a$

D. $|\vec{AB} + \vec{AD}| = 3 a \sqrt{3}$

Xem đáp án

Đáp án A

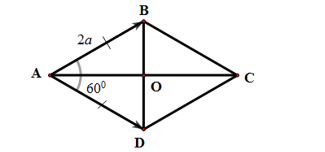
Tam giác ABD cân tại A do ABCD là hình thoi và có góc $\hat{BAD} = 60^{0}$ nên tam giác ABD đều.

Áp dụng quy tắc hình bình hành ta có:

Câu 15:

Tìm tất cả các giá trị thực của tham số m để đường thẳng y = 3x + 1 song song với đường thẳng y = ( $m^{2}$ -1)x + (m-1).

A. m = $\pm 2$

B. m = 2

C. m = -2

D. m = 0

Xem đáp án

Đáp án C

Để đường thẳng y = ( $m^{2}$ -1)x + (m – 1) song song với đường thẳng y = 3x + 1 khi:

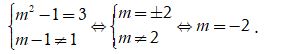
Câu 16:

Biết rằng đồ thị hàm số y = ax + b đi qua điểm N ( 4; -1) và vuông góc với đường thẳng 4x – y + 1= 0. Tính tích P = ab.

A. P = 0

B. P = $\frac{- 1}{4}$

C. P = $\frac{1}{4}$

D. P = 1

Xem đáp án

Đáp án A

Đồ thị hàm số đi qua điểm N( 4; -1) nên -1 = 4a + b (1)

Mặt khác, đồ thị hàm số vuông góc với đường thẳng 4x – y + 1 = 0 hay y = 4x + 1 nên 4a = -1 (2)

Từ (1) và (2), ta có hệ:

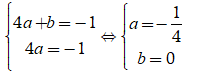
Suy ra: P = ab = 0

Câu 17:

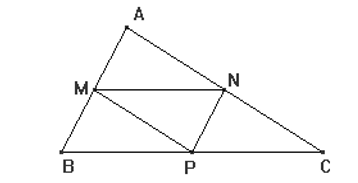
Cho hình vẽ với M,N,P lần lượt là trung điểm của AB, AC, BC. Khẳng định nào sau đây đúng?

A. $\vec{AM} = \vec{MP} - \vec{MN}$

B. $\vec{AM} = \vec{MP} + \vec{MN}$

C. $\vec{AM} = \vec{MN} - \vec{MP}$

D. $\vec{AM} = \vec{PN}$

Xem đáp án

Đáp án A

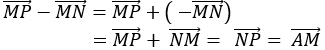
Câu 18:

Tìm a và b để đồ thị hàm số y = ax + b đi qua các điểm A (-2; 1); B(1; -2).

A. a =-2; b = -1

B. a = 2; b =1

C. a = 1; b = 1

D. a = -1; b = -1

Xem đáp án

Đáp án D

Đồ thị hàm số đi qua các điểm A (-2; 1) nên 1 = -2a + b (1)

Đồ thị hàm số đi qua các điểm B(1; -2) nên – 2 = a +b (2)

Từ (1) và (2) ta có hệ:

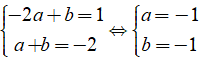
Câu 19:

Cho hàm số y = 2x + m + 1. Tìm giá trị thực của m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2.

A. m = -3

B. m = 3

C. m = 0

D. m = -1

Xem đáp án

Đáp án A

Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng -2 nên điểm B (0;-2) thuộc đồ thị hàm số.

Suy ra: 0 = 2. (-2) + m + 1 nên m = -3

Câu 20:

Cho hai góc $α$ và $β$ với α+ $β$ = $180^{0}$ . Tính giá trị của biểu thức P = cos $α$ .cos $β$ - sin $α$ .sin $β$

A. P = 0

B. P = 1

C. P = -1

D. P = 2

Xem đáp án

Đáp án C

Hai góc $α$ và $β$ bù nhau nên sin $α$ = sin $β$ và cos $α$ = -cos $β$

Do đó P = cos $α$ .cos $β$ - sin $α$ .sin $β$

=> P = - cos $β$ .cos $β$ - sin $β$ .sin $β$ = -( $\cos^{2} β$ + $\sin^{2} β$ ) = -1

Câu 21:

Cho hàm số y = x - 1 có đồ thị là đường $(∆)$ . Đường thẳng Delta tạo với hai trục tọa độ một tam giác có diện tích S bằng bao nhiêu?

A. $S = \frac{1}{2}$

B. $S = 1$

C. $S = 2$

D. $S = \frac{3}{2}$

Xem đáp án

Đáp án A

Giao điểm của $(∆)$ với trục hoành, trục tung lần lượt là A (1;0); B(0;-1).

Ta có: OA = 1; OB = 1

Diện tích tam giác vuông OAB là

Câu 22:

Tính tổng $\vec{MN} + \vec{PQ} + \vec{RN} + \vec{NP} + \vec{QR}$

A. $\vec{MR}$

B. $\vec{MN}$

C. $\vec{PR}$

D. $\vec{MP}$

Xem đáp án

Đáp án B

Ta có:

Câu 23:

Cho hình vuông ABCD có cạnh bằng a. Khi đó $|\vec{AB} + \vec{AD}|$ bằng:

A. $a \sqrt{2}$

B. $\frac{a \sqrt{2}}{2}$

C. 2a

D. a

Xem đáp án

Đáp án A

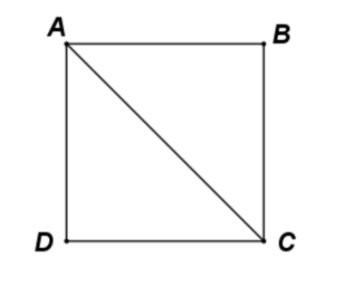
Áp dụng quy tắc hình bình hành ta có:

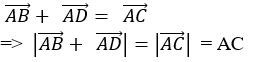
+ Ta tính AC:

Áp dụng định lí Pytago vào tam giác vuông ABC ta có:

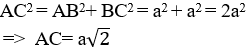
Vậy $|\vec{A B} + \vec{A D}| = \sqrt{2} a$

Câu 24:

Cho tam giác ABC vuông cân tại A có AB = a. Tính $\vec{CA} . \vec{CB}$

A. $a^{2}$

B. a

C. 2a

D. 2 $a^{2}$

Xem đáp án

Đáp án A

Do tam giác vuông cân tại A nên AB = AC = a và BC = a $\sqrt{2}$ và góc C = $45^{0}$

Ta có:

Câu 25:

Trong mặt phẳng tọa độ cho điểm M(1; 0) và N(4; m). Tìm m để khoảng cách hai điểm đó là 5?

A. m =3

B. m = 1 hoặc m = 3

C. m = 2 hoặc m = - 4

D. m = 4 hoặc m = -4

Xem đáp án

Câu 26:

Cho biết $cosα = \frac{- 2}{3}$ . Giá trị của biểu thức E = $\frac{cotα - 3 tanα}{2 cotα - tanα}$ bằng bao nhiêu?

A. $\frac{- 25}{3}$

B. $\frac{11}{3}$

C. $\frac{- 11}{3}$

D. $\frac{16}{3}$

Xem đáp án

Đáp án C

Nhân cà tử và mẫu với tanα và chú ý tanα.cotα= 1 ta được:

Câu 27:

Cho các vectơ $\vec{α} (1; - 2)$ ; $\vec{b} (- 2; - 6)$ . Khi đó góc giữa chúng là

A. $45^{0}$

B. $60^{0}$

C. $30^{0}$

D. $135^{0}$

Xem đáp án

Đáp án A

Câu 28:

Cho tam giác ABC với G là trọng tâm. Đặt $\vec{CA} = \vec{a}$ , $\vec{CB} = \vec{b}$ . Khi đó, $\vec{AG}$ được biểu diễn theo hai vectơ a và b là

A. $\vec{AG} = \frac{\vec{a} - 2 \vec{b}}{3}$

B. $\vec{AG} = \frac{2 \vec{a} + \vec{b}}{3}$

C. $\vec{AG} = \frac{2 \vec{a} - \vec{b}}{3}$

D. $\vec{AG} = \frac{- 2 \vec{a} + \vec{b}}{3}$

Xem đáp án

Đáp án D

Do G là trọng tâm tam giác ABC nên:

Câu 29:

Tổng các nghiệm của phương trình $|2 x - 5| + |2 x^{2} - 7 x + 5| = 0$ bằng:

A. 6

B. $\frac{5}{2}$

C. $\frac{7}{2}$

D. $\frac{3}{2}$

Xem đáp án

Đáp án B

Ta có:

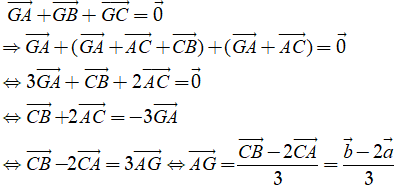
Câu 30:

Phương trình ${(x + 1)}^{2} - 3 |x + 1| + 2 = 0$ có bao nhiêu nghiệm?

A. 0.

B.1.

C. 2.

D. 4.

Xem đáp án

Đáp án D

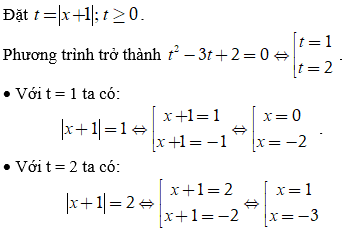
Vậy phương trình có bốn nghiệm là x = -3; x = -2; x = 0; x = 1

Câu 31:

Cho 2 vectơ $\vec{a}; \vec{b}$ có $|\vec{a}|$ =4; $|\vec{b}|$ =5; ( $\vec{a}; \vec{b}$ )= $120^{0}$ . Tính: $|\vec{a} + \vec{b}|$

A. $\sqrt{21}$

B. $\sqrt{61}$

C. 21

D. 61

Xem đáp án

Đáp án A

Ta có:

Câu 32:

Cho hàm số y = $x^{2}$ - 2x + 3. Trong các mệnh để sau đây, tìm mệnh đề đúng?

A. y tăng trên khoảng (0;+ $\infty$ )

B. y giảm trên khoảng (- $\infty$ ;2)

C. Đồ thị của y có đỉnh I(1;0)

D. y tăng trên khoảng (1;+ $\infty$ )

Xem đáp án

Đáp án D

Do a = 1 > 0; $\frac{- b}{2 a}$ = 1 nên hàm số tăng trên (1; + ∞).

Đồ thị có đỉnh là I(1; 2)

Câu 33:

Có bao nhiêu giá trị nguyên của tham số m thuộc [-5; 5] để phương trình $x^{2}$ + 4mx + $m^{2}$ có hai nghiệm âm phân biệt?

A. 5

B. 6

C. 10

D. 11

Xem đáp án

Đáp án A

Câu 34:

Giả sử phương trình $x^{2}$ - 3x - m = 0 (m là tham số) có hai nghiệm là $x_{1}$ ; $x_{2}$ . Tính giá trị biểu thức P = $x_{1}^{2}$ (1- $x_{2}$ ) + $x_{2}^{2}$ (1- $x_{1}$ ) theo m.

A. P = - m + 9

B. P = 5m + 9

C. P = m + 9

D. P = - 5m + 9

Xem đáp án

Câu 35:

Tập nghiệm của phương trình $\frac{x^{2} - 5 x}{\sqrt{x - 2}} = \frac{- 4}{\sqrt{x - 2}}$ là:

A. S = {1;4}

B. S = {1}

C. S = $\emptyset$

D. S = {4}

Xem đáp án

Câu 36:

Đường thẳng nào trong các đường thẳng sau đây là trục đối xứng của parabol y = $- 2 x^{2}$ + 5x + 3?

A. x = $\frac{5}{2}$

B. x = $\frac{- 5}{2}$

C. x = $\frac{5}{4}$

D. x = $\frac{- 5}{4}$

Xem đáp án

Đáp án C

Đồ thị hàm số có trục đối xứng là:

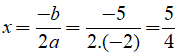
Câu 37:

Phương trình $x (x^{2} - 1) \sqrt{x - 1} = 0$ có bao nhiêu nghiệm?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B

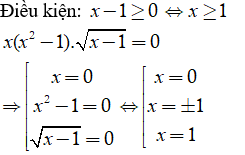
Đối chiếu điều kiện, ta được nghiệm của phương trình đã cho là x = 1

Vậy phương trình đã cho có nghiệm duy nhất.

Câu 38:

Phương trình ${mx}^{2}$ + 6 = 4x + 3m có nghiệm duy nhất khi:

A. $m \in \emptyset$

B. $m = 0$

C. $m \in R$

D. $m \neq 0$

Xem đáp án

Đáp án B

Phương trình ${mx}^{2}$ + 6 = 4x + 3m viết lại (*)

- Với m = 0.

Khi đó, phương trình trở thành -4x + 6 = 0 $\Leftrightarrow x = \frac{3}{2}$

Do đó, m = 0 là một giá trị cần tìm.

- Với $m \neq 0$ , phương trình (*) là phương trình bậc hai ẩn x

Ta có:

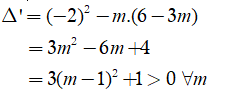
Khi đó, phương trình đã cho luôn có hai nghiệm phân biệt nên $m \neq 0$ không thỏa mãn.

Câu 39:

Tìm tất cả các giá trị thực của tham số m để phương trình $3 x^{2}$ - (m+2)x + m - 1 = 0 có một nghiệm gấp đôi nghiệm còn lại.

A. $m \in \{\frac{5}{2}; 7\}$

B. $m \in \{- 2; - \frac{1}{2}\}$

C. $m \in \{- \frac{3}{4}; 1\}$

D. $m \in \{0; \frac{2}{5}\}$

Xem đáp án

Đáp án A

Phương trình có hai nghiệm phân biệt

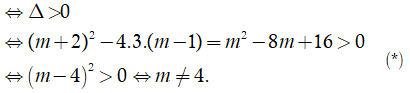
Theo đinh lí Viet, ta có:

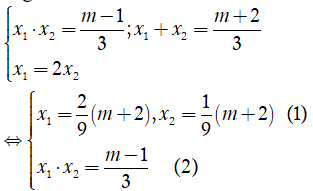
Thay (1) vào (2) ta được:

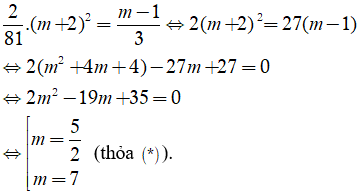
Câu 40:

Cho parabol (P): y = a $x^{2}$ + bx + 2 biết rằng parabol đó đi qua hai điểm A(1;5) và B(-2;8). Parabol đó là:

A. y = $x^{2}$ - 4x + 2

B. y = - $x^{2}$ + 2x + 2

C. y = 2 $x^{2}$ + x + 2

D. y = 2 $x^{2}$ + x + 1

Xem đáp án

Đáp án C

Parabol đó đi qua hai điểm A(1;5) và B(-2;8) nên:

Câu 41:

Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho $AM = \frac{AC}{4}$ . Gọi N là trung điểm của đoạn thẳng DC. Tính $\vec{MB} . \vec{MN}$

A. - 4

B. 0

C. 4

D. 16

Xem đáp án

Đáp án B

Ta phân tích các vectơ $\vec{MB}; \vec{MN}$ theo các vectơ có giá vuông góc với nhau.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Toán lớp 10 Học kì 1 năm 2020 - 2021 có đáp án (Đề 1)

Đề thi Toán lớp 10 Học kì 1 năm 2020 - 2021 có đáp án (Đề 3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương