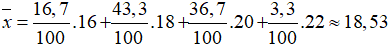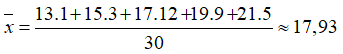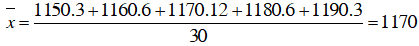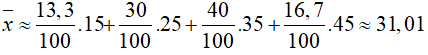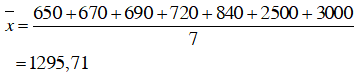Bài3: Số trung bình cộng. Số trung vị. Mốt
-
1007 lượt thi
-
7 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Cho bảng phân bố tần số và tần suất ghép lớp sau:
Nhiệt độ trung bình của tháng 12 tại thành phố Vinh
từ 1961 đến hết 1990 (30 năm)
| Lớp nhiệt độ (oC) | Tần số | Tần suất (%) |
| [12; 14) | 1 | 3,33 |
| [14; 16) | 3 | 10,00 |
| [16; 18) | 12 | 40,00 |
| [18; 20) | 9 | 30,00 |
| [20; 22] | 5 | 16,67 |
| Cộng | 30 | 100 % |
a) Hãy tính số trung bình cộng của bảng 6 và bảng 8.
b) Từ kết quả đã tính được ở câu a), có nhận xét gì về nhiệt độ ở thành phố Vinh
trong tháng 2 và tháng 12 (của 30 năm được khảo sát).
 Xem đáp án
Xem đáp án
a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
Số trung bình cộng của bảng 8 là:
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ
trung bình trong tháng 2 khoảng 0,6ºC.
Câu 2:
Trong bảng phân bố tần số, các số liệu thống kê đã được sắp thứ tự
thành dãy không giảm theo các giá trị của chúng.
Hãy tìm số trung vị của các số liệu thống kê cho ở bảng 9.
Số áo bán được trong một quý ở một quý ở một cửa hàng bán áo sơ mi nam
| Cỡ số | 36 | 37 | 38 | 39 | 40 | 41 | 42 | Cộng |
| Tần số (số áo bán được) | 13 | 45 | 126 | 110 | 126 | 40 | 5 | 465 |
 Xem đáp án
Xem đáp án
Ta sắp xếp dãy số áo bán được theo dãy tăng dần:
36, 36, 36, …, 36, 37, 37, …, 37, 38, 38, …, 38, …., 42, 42.
Dãy số gồm 465 số nên số trung vị là số đứng ở vị trí thứ 233.
Số thứ 233 là số 39.
Vậy Me = 39.
Câu 3:
Tính số trung bình cộng của các bảng phân bố đã được lập ở các
bài tập số 1 và số 2 của Bài 1.
 Xem đáp án
Xem đáp án
Bài 1: Bảng phân bố tần số tuổi thọ của 30 bóng đèn điện.
| Tuổi thọ | Tần số |
| 1150 | 3 |
| 1160 | 6 |
| 1170 | 12 |
| 1180 | 6 |
| 1190 | 3 |
| Cộng | 30 |
Số trung bình:
Bài 2: Bảng phân bố tần suất ghép lớp độ dài của 60 lá dương sỉ trưởng thành:
| Lớp của độ dài (cm) | Tần suất | Giá trị đại diện |
| [10; 20) | 13,3 | 15 |
| [20; 30) | 30,0 | 25 |
| [30; 40) | 40,0 | 35 |
| [40; 50) | 16,7 | 45 |
| Cộng | 100 (%) |
Số trung bình:
Câu 4:
Trong một trường THPT, để tìm hiểu tình hình học môn Toán của hai lớp
10A, 10B, người ta cho hai lớp đó đồng thời làm bài thi môn toàn theo
cùng một đề thi và lập được hai bảng phân bố tần số ghép lớp sau đây:
Điểm thi Toán của lớp 10A
| Lớp điểm thi | Tần số |
|---|---|
| [0; 2) | 2 |
| [2; 4) | 4 |
| [4; 6) | 12 |
| [6; 8) | 28 |
| [8; 10] | 4 |
| Cộng | 50 |
Điểm thi Toán của lớp 10B
| Lớp điểm thi | Tần số |
|---|---|
| [0; 2) | 4 |
| [2; 4) | 10 |
| [4; 6) | 18 |
| [6; 8) | 14 |
| [8; 10] | 5 |
| Cộng | 51 |
Hãy tính số trung bình cộng của hai bảng phân bố ở trên và nêu nhận xét
về kết quả làm bài thi của hai lớp.
 Xem đáp án
Xem đáp án
Nhận xét: Số trung bình cộng điểm thi Toán của lớp 10A cao hơn lớp 10B
nên có thể nói lớp 10A có kết quả thi môn Toán tốt hơn lớp 10B.
Câu 5:
Điều tra tiền lương hàng tháng của 30 công nhân ở một xưởng may, ta có
bảng phân bố tần số sau:
Tiền lương của 30 công nhân xưởng may
| Tiền lương(nghìn đồng) | Tần số |
|---|---|
| 300 | 3 |
| 500 | 5 |
| 700 | 6 |
| 800 | 5 |
| 900 | 6 |
| 100 | 5 |
| Cộng | 30 |
Tìm mốt của bảng phân bố trên. Nếu ý nghĩa của kết quả tìm được.
 Xem đáp án
Xem đáp án
Trong bảng phân bố trên, hai giá trị 700 và 900 có cùng tần số
lớn nhất là 6. Do đó ta có hai mốt là:
M0(1) = 700; M0(2) = 900.
Ý nghĩa:
+ Số công nhân có tiền lương 700.000đ/tháng và 900.000đ/tháng
bằng nhau và chiếm đa số.
+ Tỉ lệ công nhân có mức lương 700 nghìn đồng / tháng và 900
nghìn đồng/ tháng cao hơn tỉ lệ công nhân có các mức lương khác.
Câu 6:
Tiền lương hàng tháng của 7 nhân viên trong một công ty du lịch là:
650, 840, 690, 720, 2500, 3000 (đơn vị: nghìn đồng).
Tìm số trung vị của các số liệu đã thống kê đã cho. Nếu ý nghĩa
của kết quả đã tính được.
 Xem đáp án
Xem đáp án
Bảng số liệu có 7 giá trị, sắp các giá trị theo thứ tự không giảm ta có:
650, 670, 690, 720, 840, 2500, 3000.
Vì số phần tử = 7 là số lẻ nên số trung vị là Me = 720 (số chính giữa của dãy).
Ý nghĩa:
Số trung bình này chênh lệch quá lớn so với các số liệu nên không đại diện
được cho các số liệu.
Trong trường hợp này, số trung vị nên được chọn làm giá trị đại diện
cho mức lương.
Câu 7:
Cho biết tình hình thu hoạch lúa vụ mùa năm 1980 của ba hợp tác xã
ở địa phương V như sau:
| Hợp tác xã | Năng suất lúa(tạ/ha) | Diện tích trồng lúa(ha) |
|---|---|---|
| A | 40 | 150 |
| B | 38 | 130 |
| C | 36 | 120 |
Hãy tính năng suất lúa trung bình của vụ mùa năm 1980 trong toàn bộ
ba hợp tác xã kể trên.
 Xem đáp án
Xem đáp án
Ta biết sản lượng thu được = năng suất . diện tích.
Sản lượng lúa của HTX A là: 40.150 = 6000 (tạ)
Sản lượng lúa của HTX B là : 38.130 = 4940 (tạ)
Sản lượng lúa của HTX C là : 36.120 = 4320 (tạ)
Tổng sản lượng lúa của cả ba HTX là : 6000 + 4940 + 4320 = 15260 (tạ)
Tổng diện tích trồng của cả ba HTX là : 150 + 130 + 120 = 400 (ha)
Năng suất lúa trung bình của cả ba HTX : 15260 : 400 = 38,15 (tạ/ha)
*Lưu ý: Các bạn không thể tính năng suất trung bình bằng cách :
(40 + 38 + 36)/3 = 38 (tạ/ha)
vì khi chênh lệch diện tích lớn thì số trung bình càng không chính xác.