15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Thông hiểu)

Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án

Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Thông hiểu)

2305 lượt thi
15 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho

$A . B M = 1, 5 a$

$B . B M = a \sqrt{2}$

$C . B M = a \sqrt{3}$

$D . B M = \frac{a \sqrt{5}}{2}$

Xem đáp án

Câu 2:

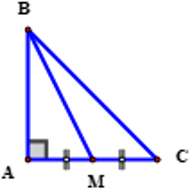
Tam giác ABC có ba cạnh là 5, 12, 13. Khi đó, diện tích tam giác là:

A. 30

$B . 20 \sqrt{2}$

$C . 10 \sqrt{3}$

D. 20

Xem đáp án

+ Ta có: $p = \frac{a + b + c}{2} = \frac{5 + 12 + 13}{2} = 15$

+ $S = \sqrt{p (p - a) (p - b) (p - c)}$

$= \sqrt{15.10.3.2} = \sqrt{900} = 30$

Đáp án cần chọn là: A

Câu 3:

Tam giác ABC có a = 21, b = 17, c = 10. Diện tích của tam giác ABC bằng:

$A . S_{Δ A B C} = 16$

$B . S_{Δ A B C} = 48$

$C . S_{Δ A B C} = 24$

$D . S_{Δ A B C} = 84$

Xem đáp án

Câu 4:

Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và $\hat{A C B} = 60^{0}$ . Tính độ dài cạnh BC

$A . B C = 3 + 3 \sqrt{6}$

$B . B C = 3 \sqrt{6} - 3$

$C . B C = 3 \sqrt{7}$

$D . B C = \frac{3 + 3 \sqrt{33}}{2}$

Xem đáp án

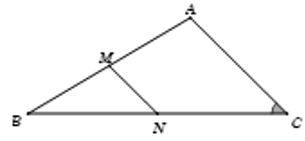
Gọi M, N lần lượt là trung điểm của AB, BC.

⇒ MN là đường trung bình của ΔABC.

⇒ MN = $\frac{1}{2}$ AC. Mà MN = 3, suy ra AC = 6.

Theo định lí hàm cosin, ta có

AB²= AC²+ BC²− 2.AC.BC.cos $\hat{A C B}$

⇔ 9²= 6²+ BC²− 2.6.BC.cos60⁰

⇒ BC = 3+3 $\sqrt{6}$

Đáp án cần chọn là: A

Câu 5:

Tam giác ABC có AB = 4, BC = 6, AC = 2 $\sqrt{7}$ . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM?

$A . A M = 4 \sqrt{2}$

$B . A M = 3$

$C . A M = 2 \sqrt{3}$

$D . A M = 3 \sqrt{2}$

Xem đáp án

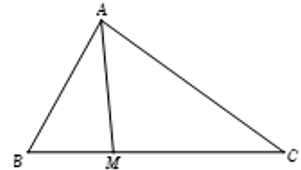
Theo định lí hàm cosin, ta có:

$\cos B = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C}$

$= \frac{4^{2} + 6^{2} - {(2 \sqrt{7})}^{2}}{2.4.6} = \frac{1}{2}$

Do MC = 2MB $\Rightarrow B M = \frac{1}{3} B C = 2$

Theo định lí hàm cosin, ta có:

$A M^{2} = A B^{2} + B M^{2} - 2. A B . B M . \cos \hat{B}$

$= 4^{2} + 2^{2} - 2.4.2. \frac{1}{2} = 12$

$\Rightarrow A M = 2 \sqrt{3}$

Đáp án cần chọn là: C

Câu 6:

Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích tam giác mới được tạo nên bằng:

A. 2S

B. 3S

C. 4S

D. 6S

Xem đáp án

+ Có $S = \frac{1}{2} B C . C A . \sin C$

+ Gọi S’ là diện tích tam giác khi tăng cạnh BC lên 2 lần đồng thời tăng cạnh CA lên 3 lần và giữ nguyên độ lớn của góc C, ta có:

$S' = \frac{1}{2} .2 B C .3 C A . \sin C = 6 S$

Đáp án cần chọn là: D

Câu 7:

Tam giác ABC có BC = 10 và $\hat{A} = 30^{0}$ . Khi đó, bán kính đường tròn ngoại tiếp tam giác ABC là:

A. 5

B. 10

$C . \frac{10}{\sqrt{3}}$

$D . 10 \sqrt{3}$

Xem đáp án

Từ $\frac{B C}{\sin A} = 2 R \Rightarrow R = \frac{B C}{2 \sin A} = \frac{10}{2 \sin 30^{0}} = 10$

Đáp án cần chọn là: B

Câu 8:

Cho tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng 64cm². Giá trị $\sin \hat{A}$ là:

$A . \frac{\sqrt{3}}{2}$

$B . \frac{3}{8}$

$C . \frac{4}{5}$

$D . \frac{8}{9}$

Xem đáp án

Ta có: $S = \frac{1}{2} A B . A C . \sin A \Rightarrow \sin A = \frac{2 S}{A B . A C} = \frac{2.64}{8.18} = \frac{8}{9}$

Đáp án cần chọn là: D

Câu 9:

Hình bình hành ABCD có AB = a, $B C = a \sqrt{2}$ và $\hat{B A D} = 45^{0}$ . Khi đó hình bình hành có diện tích bằng:

$A . 2 a^{2}$

$B . a^{2} \sqrt{2}$

$C . a^{2}$

$D . a^{2} \sqrt{3}$

Xem đáp án

Câu 10:

Tam giác ABC có AB = 5, BC = 7, CA = 8. Số đo góc $\hat{A}$ bằng:

A. 30⁰

B. 45⁰

C. 60⁰

D. 90⁰

Xem đáp án

Theo định lí hàm cosin, ta có:

$\cos \hat{A} = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{5^{2} + 8^{2} - 7^{2}}{2.5.8} = \frac{1}{2}$

Do đó, $\hat{A} = 60^{0}$

Đáp án cần chọn là: C

Câu 11:

Tam giác ABC có ba cạnh là 6, 8, 10. Khi đó, bán kính đường tròn nội tiếp tam giác ABC là:

$A . \sqrt{3}$

B. 4

C. 2

D. 1

Xem đáp án

Câu 12:

Tam giác ABC vuông tại A có AB = 6cm, BC = 10cm. Tính bán kính r của đường tròn nội tiếp tam giác đã cho

A. r=1cm

$B . r = \sqrt{2} cm$

C. r=2cm

D. r=3cm

Xem đáp án

Câu 13:

Tam giác ABC có AB = 5, AC = 8, và $\hat{B A C} = 60^{0}$ . Tính bán kính r của đường tròn nội tiếp tam giác đã cho

A. r=1

B. r=2

$C . r = \sqrt{3}$

$D . r = 2 \sqrt{3}$

Xem đáp án

Câu 14:

Tam giác ABC có a = 21, b = 17, c = 10. Tính bán kính r của đường tròn nội tiếp tam giác đã cho

A. r=16

B. r=7

$C . r = \frac{7}{2}$

D. r=8

Xem đáp án

Câu 15:

Tính bán kính r của đường tròn nội tiếp tam giác đều cạnh a

$A . r = \frac{a \sqrt{3}}{4}$

$B . r = \frac{a \sqrt{2}}{5}$

$C . r = \frac{a \sqrt{3}}{6}$

$D . r = \frac{a \sqrt{5}}{7}$

Xem đáp án

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án

Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương