15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 Bài 2. Định lí côsin và định lí sin có đáp án

Câu 1:

Tam giác ABC có $B C = 5 \sqrt{5}, A C = 5 \sqrt{2}, A B = 5$ . Số đo góc $\hat{A}$ là:

A. 30°;

B. 45°;

C. 120°;

D. 135°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:

$\cos A = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{5^{2} + {(5 \sqrt{2})}^{2} - {(5 \sqrt{5})}^{2}}{2.5.5 \sqrt{2}} = - \frac{\sqrt{2}}{2}$

$\Rightarrow \hat{A} = 135 ° .$

Vậy $\hat{A} = 135 ° .$

Câu 2:

Tam giác ABC có $\hat{A} = 105 °, \hat{B} = 45 °$ , AC = 10. Độ dài cạnh AB là:

A. $\frac{5 \sqrt{6}}{2};$

B. $5 \sqrt{2};$

C. $5 \sqrt{6};$

D. $10 \sqrt{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Xét tam giác ABC có $\hat{A} = 105 °, \hat{B} = 45 °$ ta có:

$\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong tam giác)

$\Rightarrow \hat{C} = 180 ° - \hat{A} - \hat{B}$

$\Rightarrow \hat{C} = 180 ° - 105 ° - 45 ° = 30 °$

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{A C}{\sin B} = \frac{A B}{\sin C}$

$\Rightarrow \frac{10}{\sin 45 °} = \frac{A B}{\sin 30 °} \Rightarrow A B = \frac{10. \sin 30 °}{\sin 45 °} = 5 \sqrt{2} .$

Vậy $A B = 5 \sqrt{2} .$

Câu 3:

Tam giác ABC có $A C = 3 \sqrt{3},$ AB = 3, BC = 6. Số đo góc B là:

A. 30°;

B. 45°;

C. 60°;

D. 120°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:

$\cos B = \frac{A B^{2} + B C^{2} - A C^{2}}{2. A B . B C} = \frac{3^{2} + 6^{2} - {(3 \sqrt{3})}^{2}}{2.3.6} = \frac{1}{2}$

$\Rightarrow \hat{B} = 60 ° .$

Câu 4:

Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, $A C = R \sqrt{2} .$ Tính số đo của $\hat{A}$ biết $\hat{A}$ là góc tù.

A. 105°;

B. 120°;

C. 135°;

D. 150°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Trong tam giác ABC có $\hat{A}$ là góc tù nên $\hat{B}, \hat{C}$ là góc nhọn.

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{A C}{\sin B} = \frac{A B}{\sin C} = 2 R$

$\Rightarrow \frac{R \sqrt{2}}{\sin B} = \frac{R}{\sin C} = 2 R$

$\Rightarrow \{\begin{cases} \sin B = \frac{R \sqrt{2}}{2 R} = \frac{\sqrt{2}}{2} \\ s i n C = \frac{R}{2 R} = \frac{1}{2} \end{cases}$ $\Rightarrow \{\begin{cases} \hat{B} = 45 ° \\ \hat{C} = 30 ° \end{cases}$ (vì $\hat{B}, \hat{C}$ là góc nhọn)

Xét tam giác ABC có $\hat{B} = 45 °, \hat{C} = 30 °$ ta có:

$\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong tam giác)

$\Rightarrow \hat{A} = 180 ° - \hat{B} - \hat{C}$

$\Rightarrow \hat{A} = 180 ° - 45 ° - 35 ° = 105 °$

Vậy $\hat{A} = 105 °$

Câu 5:

Tam giác ABC có ba cạnh lần lượt là: 2, 3, 4. Góc nhỏ nhất của tam giác có côsin bằng bao nhiêu?

A. $\frac{\sqrt{15}}{8};$

B. $\frac{7}{8};$

C. $\frac{1}{2}$

D. $\frac{\sqrt{14}}{8} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Góc nhỏ nhất ứng với cạnh đối diện có độ dài nhỏ nhất.

Giả sử tam giác ABC có AB = 2, AC = 3, BC = 4. Khi đó góc nhỏ nhất là góc C ứng với cạnh đối diện AB.

Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:

$\cos C = \frac{A C^{2} + B C^{2} - A B^{2}}{2. A C . B C} = \frac{3^{2} + 4^{2} - 2^{2}}{2.3.4} = \frac{7}{8} .$

Vậy côsin của góc nhỏ nhất trong tam giác bằng $\frac{7}{8}$

Câu 6:

Diện tích của tam giác ABC với $\hat{A} = 60 °,$ AB = 20, AC = 10 là:

A. 50;

B.

50 \sqrt{2};

C.

50 \sqrt{3}

D.

50 \sqrt{5} .

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Diện tích tam giác ABC là:

$S = \frac{1}{2} . A B . A C . \sin A = \frac{1}{2} .20.10. \sin 60 ° = 50 \sqrt{3}$ (đơn vị diện tích).

Vậy

S = 50 \sqrt{3}

(đơn vị diện tích).

Câu 7:

Diện tích tam giác có ba cạnh lần lượt là $\sqrt{3}, \sqrt{2}$ và 1 là:

A. $\frac{\sqrt{2}}{2};$

B. $\sqrt{3};$

C. $\frac{\sqrt{3}}{2};$

D. $\frac{\sqrt{6}}{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Nửa chu vi tam giác có độ dài ba cạnh $\sqrt{3}, \sqrt{2}$ , 1 là: $p = \frac{\sqrt{3} + \sqrt{2} + 1}{2}$

Diện tích tam giác theo công thức Heron là: $S = \sqrt{p . (p - \sqrt{3}) . (p - \sqrt{2}) . (p - 1)} = \frac{\sqrt{2}}{2}$

Vậy $S = \frac{\sqrt{2}}{2} .$

Câu 8:

Nếu tam giác ABC có BC² < AB² + AC² thì:

A.

\hat{A}

là góc nhọn;

B.

\hat{A}

là góc vuông;

C.

\hat{A}

là góc tù;

D. Không đưa ra được kết luận nào.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Áp dụng hệ quả định lí côsin trong tam giác ABC ta có:

$\cos A = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C}$

Nếu BC² < AB² + AC² thì AB² + AC² ‒ BC² > 0

Do đó $\frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} > 0$ hay cosA > 0

Mà $0 ° < \hat{A} < 180 °$

Þ Góc $\hat{A}$ là góc nhọn.

Câu 9:

Tam giác ABC có $\hat{B} + \hat{C} = 135 °$ và BC = a. Tính bán kính đường tròn ngoại tiếp tam giác.

A. $a \sqrt{3};$

B. $a \sqrt{2};$

C. $\frac{a \sqrt{3}}{2};$

D. $\frac{a \sqrt{2}}{2} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Xét tam giác ABC có $\hat{B} + \hat{C} = 135 °$ ta có:

$\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong tam giác)

$\Rightarrow \hat{A} = 180 ° - (\hat{B} + \hat{C})$

$\Rightarrow \hat{A} = 180 ° - 135 ° = 45 °$

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{B C}{\sin A} = 2 R$

$\Rightarrow R = \frac{B C}{2. \sin A} = \frac{a}{2. \sin 45 °} = \frac{a}{2. \frac{\sqrt{2}}{2}} = \frac{a}{\sqrt{2}} = \frac{a \sqrt{2}}{2}$

Vậy bán kính đường tròn ngoại tiếp tam giác ABC là: $R = \frac{a \sqrt{2}}{2} .$

Câu 10:

Tam giác ABC có AB = 10, AC = 24, diện tích bằng 120. Độ dài đường trung tuyến AM là:

A.

7 \sqrt{3};

B. 13;

C.

11 \sqrt{2};

D. 26

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Diện tích tam giác ABC là: $S = \frac{1}{2} . A B . A C . \sin A$

$\Rightarrow \sin A = \frac{2 S}{A B . A C} = \frac{2.120}{10.24} = 1$

Mà $0 ° < \hat{A} < 180 °$

$\Rightarrow \hat{A} = 90 °$

Þ DABC vuông tại A

Xét tam giác ABC vuông tại A, theo định lí Py – ta – go ta có:

BC² = AB² + AC² Þ BC² = 10² + 24² = 676

Þ BC = 26.

Do đó trung tuyến AM ứng với cạnh huyền BC có độ dài là: $A M = \frac{1}{2} B C = \frac{1}{2} .26 = 13.$

Vậy độ dài đường trung tuyến AM bằng 13.

Câu 11:

Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Diện tích tam giác GEC là:

A.

50 \sqrt{2}

cm²;

B. 50 cm²;

C. 75 cm²;

D.

15 \sqrt{105}

cm².

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

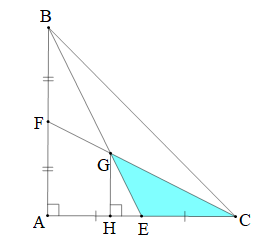
Vì BE là trung tuyến của tam giác ABC nên E là trung điểm của AC.

Do đó $E C = \frac{1}{2} . A C = \frac{1}{2} .30 = 15 (c m)$

Hai đường trung tuyến BE và CF cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Khi đó $G E = \frac{1}{3} B E$ (tính chất trọng tâm của tam giác)

Hay $\frac{G E}{B E} = \frac{1}{3} .$

Gọi H là chân đường vuông góc kẻ từ G xuống AC.

Suy ra GH // AB.

Do đó $\frac{G H}{B A} = \frac{G E}{B E}$ (định lí Ta – let trong tam giác ABE)

Hay $\frac{G H}{B A} = \frac{1}{3} \Rightarrow G H = \frac{1}{3} . B A = \frac{1}{3} .30 = 10 (c m)$

Diện tích tam giác GEC là: $S_{G E C} = \frac{1}{2} . G H . E C = \frac{1}{2} .10.15 = 75 (c m^{2})$

Vậy diện tích tam giác GEC là 75 cm².

Câu 12:

Bán kính đường tròn nội tiếp tam giác có ba cạnh lần lượt là 5, 12, 13 là:

A. $\sqrt{2}$

B. $\sqrt{3}$

C. 2

D. $2 \sqrt{2}$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Xét tam giác có độ dài ba cạnh là 5, 12, 13 ta có: 5² + 12² = 169 và 13² = 169.

Do đó 5² + 12² = 13² nên tam giác này là tam giác vuông (định lí Py – ta – go đảo)

Diện tích tam giác này là: $S = \frac{1}{2} .5.12 = 30$ (đơn vị diện tích)

Nửa chu vi tam giác này là: $p = \frac{5 + 12 + 13}{2} = 15$

Mặt khác S = pr $p = \frac{5 + 12 + 13}{2} = 15$

Vậy bán kính đường tròn nội tiếp tam giác bằng 2.

Câu 13:

Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:

A. 2S

B. 3S

C. 4S

D. 6S

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Ta có diện tích ban đầu của tam giác ABC là: $S = \frac{1}{2} . B C . A C . \sin C$ .

Diện tích của tam giác mới sau khi thay đổi kích thước là:

$S^{'} = \frac{1}{2} .2 B C .3 A C . \sin C = 6. (\frac{1}{2} . B C . A C . \sin C) = 6 S$ .

Vậy diện tích của tam giác mới được tạo thành là 6S.

Câu 14:

Hình bình hành có một cạnh là 4, hai đường chéo là 6 và 8. Độ dài cạnh kề với cạnh có độ dài bằng 4 là:

A. 5;

B.

\sqrt{34}

C. 6;

D.

\sqrt{42}

Xem đáp án

Hướng dẫn giải

Đáp án đúng là B:

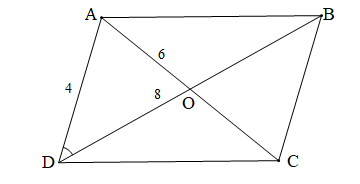
Hình bình hành có một cạnh là 4, hai đường chéo là 6 và 8 được mô tả như hình vẽ, do đó AD = 4, AC = 6, BD = 8.

Gọi O là giao điểm của hai đường chéo.

Khi đó O là trung điểm của AC và BD (tính chất hình bình hành).

Þ AO = 3 và DO = 4.

Áp dụng hệ quả định lí côsin vào tam giác ADO ta có:

$c o s \hat{A D O} = \frac{A D^{2} + D O^{2} - A O^{2}}{2. A D . D O} = \frac{4^{2} + 4^{2} - 3^{2}}{2.4.4} = \frac{23}{32}$ $\Rightarrow c o s \hat{A D B} = \frac{23}{32}$

Áp dụng định lí côsin vào tam giác ABD ta có:

AB² = AD² + BD² – 2.AD.BD. $c o s \hat{A D B}$

Þ AB² = 4² + 8² – 2.4.8. $\frac{23}{32}$ = 34

$\Rightarrow A B = \sqrt{34} .$

Vậy độ dài cạnh kề với cạnh có độ dài bằng 4 của hình bình hành đó là $\sqrt{34}$

Câu 15:

Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số $\frac{R}{r}$ là:

A. $1 + \sqrt{2}$

B. $\frac{2 + \sqrt{2}}{2};$

C. $\frac{\sqrt{2} - 1}{2};$

D. $\frac{1 + \sqrt{2}}{2} .$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Xét tam giác ABC vuông cân tại A, giả sử AB = AC = a, theo định lí Py – ta – go ta có:

BC² = AB² + AC² = a² + a² = 2a²

$\Rightarrow B C = a \sqrt{2} .$

Do đó nửa chu vi tam giác ABC là $p = \frac{A B + A C + B C}{2} = \frac{a + a + a \sqrt{2}}{2} = a . (\frac{2 + \sqrt{2}}{2})$

Tam giác ABC vuông tại A nên diện tích tam giác ABC là:

$S = \frac{1}{2} . A B . A C = \frac{1}{2} . a . a = \frac{a^{2}}{2}$ (đơn vị diện tích)

Mặt khác $S = p r = \frac{A B . A C . B C}{4 R}$

$\Rightarrow r = \frac{S}{p} = \frac{\frac{a^{2}}{2}}{a . (\frac{2 + \sqrt{2}}{2})} = \frac{a}{2 + \sqrt{2}}$ và $R = \frac{A B . A C . B C}{4 S} = \frac{a . a . a \sqrt{2}}{4. \frac{a^{2}}{2}} = \frac{a \sqrt{2}}{2}$

Do đó $\frac{R}{r} = \frac{\frac{a \sqrt{2}}{2}}{\frac{a}{2 + \sqrt{2}}} = \frac{a \sqrt{2}}{2} : \frac{a}{2 + \sqrt{2}} = \frac{a \sqrt{2}}{2} . \frac{2 + \sqrt{2}}{a} = 1 + \sqrt{2}$

Vậy $\frac{R}{r} = 1 + \sqrt{2} .$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 10 Bài 2. Định lí côsin và định lí sin có đáp án

Trắc nghiệm Toán 10 Bài 2. Định lí côsin và định lí sin có đáp án

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương